本文概述
该算法用于扫描转换线。它是由Bresenham开发的。这是一种有效的方法, 因为它仅涉及整数加法, 减法和乘法运算。这些操作可以非常快速地执行, 因此可以快速生成线。
在这种方法中, 选择的下一个像素是与真实线距离最小的那个像素。
该方法的工作方式如下:
假设有一个像素P1’(x1′, y1’), 然后选择我们可能要工作到深夜的后续像素, 在水平方向上一次朝P2’(x2′, y2’)的一个像素位置。
随时选择一个像素
下一个像素是
- 任一右侧(该行的下限)
- 顶部朝上, 朝上(该行的上限)
该线最好由距P1′, P2’之间的路径距离最小的那些像素来近似。
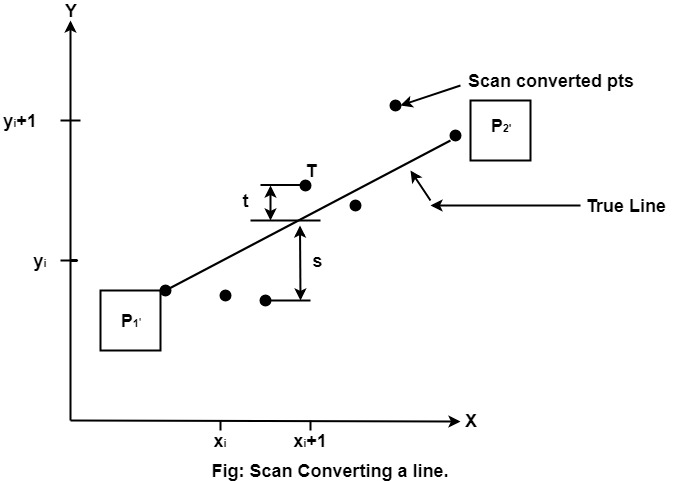
要选择底部像素S和顶部像素T之间的下一个像素。如果选择S, 则xi + 1 = xi + 1和yi + 1 = yi如果选择T, 则我们xi + 1 = xi + 1和yi + 1 = yi + 1
线在x = xi + 1处的实际y坐标为y = mxi + 1 + b
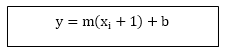
从S到y方向上的实际线的距离s = y-yi
从T到y方向上的实际线的距离t =(yi + 1)-y
现在考虑这两个距离值s-t之差
当(s-t)<0⟹s <t
最接近的像素是S
当(s-t)≥0⟹s <t
最近的像素是T
该差为s-t =(y-yi)-[(yi + 1)-y] = 2y-2yi -1
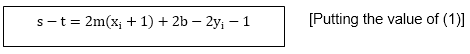
将m代入并引入决策变量di =△x(st)di =△x(2(xi + 1)+ 2b-2yi-1)= 2△xyi-2△y-1△x.2b-2yi△x -△x di = 2△y.xi-2△x.yi + c
其中c = 2△y +△x(2b-1)
我们可以在di + 1 = 2△y.xi + 1-2△x.yi + 1 + c di + 1-di = 2△y。(xi + 1- xi)-2△x(yi + 1-yi)
Since x_(i+1)=xi+1, we have di+1+di=2△y.(xi+1-xi)- 2△x(yi+1-yi)
特别案例
如果选择的像素在顶部像素T(即di≥0)⟹yi + 1 = yi + 1 di + 1 = di + 2△y-2△x
如果选择的像素在底部像素T(即di <0)⟹yi + 1 = yi di + 1 = di + 2△y
最后, 我们计算d1 d1 =△x [2m(x1 + 1)+ 2b-2y1-1] d1 =△x [2(mx1 + b-y1)+ 2m-1]
由于mx1 + b-yi = 0且m =, 我们有d1 = 2△y-△x
优点:
1.它仅涉及整数运算, 因此很简单。
2.避免了重复点的产生。
3.可以使用硬件实现, 因为它不使用乘法和除法。
4.与DDA(数字差分分析仪)相比, 它更快, 因为它不涉及DDA算法之类的浮点计算。
坏处:
1.此算法仅用于基本线条绘制。初始化不是Bresenham线条算法的一部分。因此, 要绘制平滑的线条, 你应该要研究其他算法。
布雷森汉姆线算法
步骤1:开始算法
步骤2:声明变量x1, x2, y1, y2, d, i1, i2, dx, dy
步骤3:输入x1, y1, x2, y2的值, 其中x1, y1是起点的坐标, x2, y2是终点的坐标
步骤4:计算dx = x2-x1计算dy = y2-y1计算i1 = 2 * dy计算i2 = 2 *(dy-dx)计算d = i1-dx
步骤5:将(x, y)作为起点, 将xend视为x的最大可能值。如果dx <0则x = x2 y = y2 xend = x1如果dx> 0则x = x1 y = y1 xend = x2
步骤6:在(x, y)坐标处生成点。
步骤7:检查是否生成了整行。如果x> = xend停止。
步骤8:计算下一个像素的坐标如果d <0, 则d = d + i1如果d≥0, 则d = d + i2增量y = y + 1
步骤9:递增x = x + 1
步骤10:绘制最新(x, y)坐标点
步骤11:前往步骤7
步骤12:算法结束
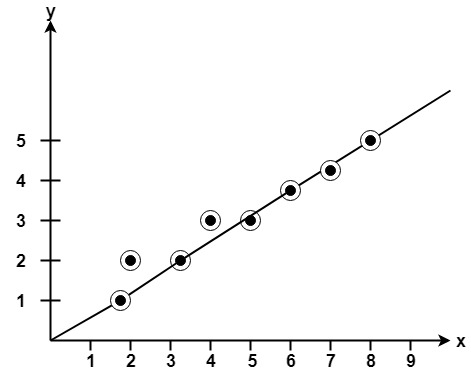
示例:行的开始和结束位置是(1, 1)和(8, 5)。寻找中间点。
解决方案:x1 = 1 y1 = 1 x2 = 8 y2 = 5 dx = x2-x1 = 8-1 = 7 dy = y2-y1 = 5-1 = 4 I1 = 2 * ∆y = 2 * 4 = 8 I2 = 2 *(Δy-Δx)= 2 *(4-7)=-6 d =I1-Δx= 8-7 = 1
| X | 和 | d = d + I1或I2 |
|---|---|---|
| 1 | 1 | d + I2 = 1 +(-6)=-5 |
| 2 | 2 | d + I1 = -5 + 8 = 3 |
| 3 | 2 | d + I2 = 3 +(-6)=-3 |
| 4 | 3 | d + I1 = -3 + 8 = 5 |
| 5 | 3 | d + I2 = 5 +(-6)=-1 |
| 6 | 4 | d + I1 = -1 + 8 = 7 |
| 7 | 4 | d + I2 = 7 +(-6)= 1 |
| 8 | 5 |
实施布雷森汉姆画线算法的程序:
#include<stdio.h>
#include<graphics.h>
void drawline(int x0, int y0, int x1, int y1)
{
int dx, dy, p, x, y;
dx=x1-x0;
dy=y1-y0;
x=x0;
y=y0;
p=2*dy-dx;
while(x<x1)
{
if(p>=0)
{
putpixel(x, y, 7);
y=y+1;
p=p+2*dy-2*dx;
}
else
{
putpixel(x, y, 7);
p=p+2*dy;}
x=x+1;
}
}
int main()
{
int gdriver=DETECT, gmode, error, x0, y0, x1, y1;
initgraph(&gdriver, &gmode, "c:\\turboc3\\bgi");
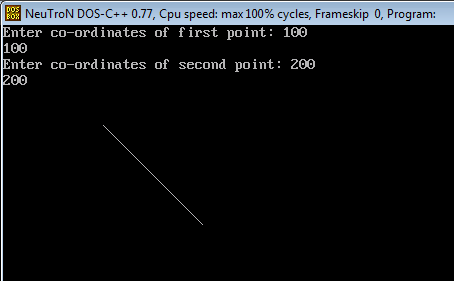
printf("Enter co-ordinates of first point: ");
scanf("%d%d", &x0, &y0);
printf("Enter co-ordinates of second point: ");
scanf("%d%d", &x1, &y1);
drawline(x0, y0, x1, y1);
return 0;
}输出:
DDA算法与布雷森汉姆线算法之间的区别
| DDA算法 | 布雷森汉姆线算法 |
|---|---|
| 1. DDA算法使用浮点运算, 即实数运算。 | 1. Bresenham的Line算法使用固定点, 即整数算术 |
| 2. DDA算法使用乘法和除法运算 | 2.Bresenham的Line算法仅使用减法和加法运算 |
| 3. DDA算法在线条图中比布雷森汉姆的线条算法慢, 因为它使用了实数算法(浮点运算) | 3. Bresenham的算法比DDA算法更快, 因为它只在计算中涉及加法和减法, 并且仅使用整数算法。 |
| 4. DDA算法不如Bresenham的Line算法准确, 高效。 | 4. Bresenham的Line算法比DDA算法更准确, 更高效。 |
| 5.DDA算法可以绘制圆和曲线, 但不如布雷森汉姆的直线算法精确 | 5. Bresenham的Line算法比DDA算法更精确地绘制圆和曲线。 |
 srcmini
srcmini
评论前必须登录!
注册