使用多项式方法定义一个圆

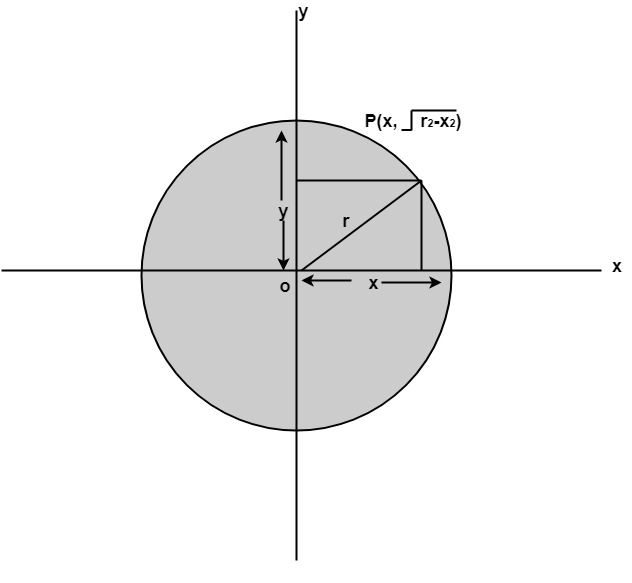
第一种方法使用二阶多项式方程式定义一个圆, 如图所示：

y2 = r2-x2其中x = x坐标y = y坐标r =圆半径

使用该方法, 可通过将x从0步进到90°来找到扇形中从90°到45°的每个x坐标。

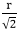
＆通过评估找到每个y坐标

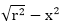
对于x的每个步骤。

算法

步骤1：设置初始变量r =圆半径（h, k）=圆心坐标x = o I =步长xend =

步骤2：测试以确定整个圆是否已被扫描转换。

如果x> x

然后停下来。

步骤3：计算y =

步骤4：绘制关于当前（x, y）坐标上的中心（h, k）对称找到的八个点。

图（x + h, y + k）图（-x + h, -y + k）图（y + h, x + k）图（-y + h, -x + k）图（-y + h , x + k）图（y + h, -x + k）图（-x + h, y + k）图（x + h, -y + k）

步骤5：递增x = x + i

步骤6：转到步骤（ii）。

程序使用多项式方法绘制圆：

#include<graphics.h>
#include<conio.h>
#include<math.h>
voidsetPixel(int x, int y, int h, int k)
{
	putpixel(x+h, y+k, RED);
	putpixel(x+h, -y+k, RED);
	putpixel(-x+h, -y+k, RED);
	putpixel(-x+h, y+k, RED);
	putpixel(y+h, x+k, RED);
	putpixel(y+h, -x+k, RED);
	putpixel(-y+h, -x+k, RED);
	putpixel(-y+h, x+k, RED);
}
main()
{
	intgd=0, gm, h, k, r;
	double x, y, x2;
	h=200, k=200, r=100;
	initgraph(&gd, &gm, "C:\\TC\\BGI ");
	setbkcolor(WHITE);
	x=0, y=r;
	x2 = r/sqrt(2);
	while(x<=x2)
	{
		y = sqrt(r*r - x*x);
		setPixel(floor(x), floor(y), h, k);
		x += 1;
	}
	getch();
	closegraph();
	return 0;
}

输出：