布雷森汉姆的循环算法

使用Bresenham算法对圆进行扫描转换的工作方式如下：点从90°到45°生成, 仅在+ x＆-y方向上移动, 如图所示：

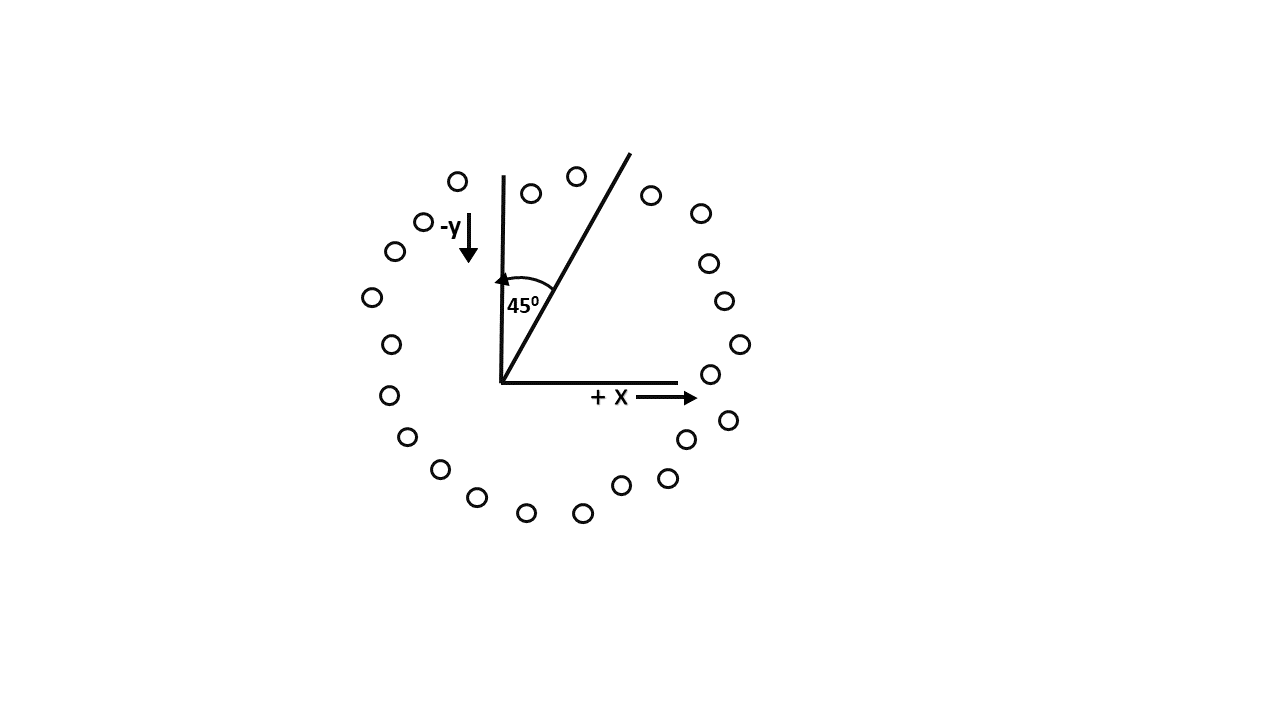
真实圆的最佳近似将由栅格中与真实圆的距离最小的那些像素描述。我们想从中产生点

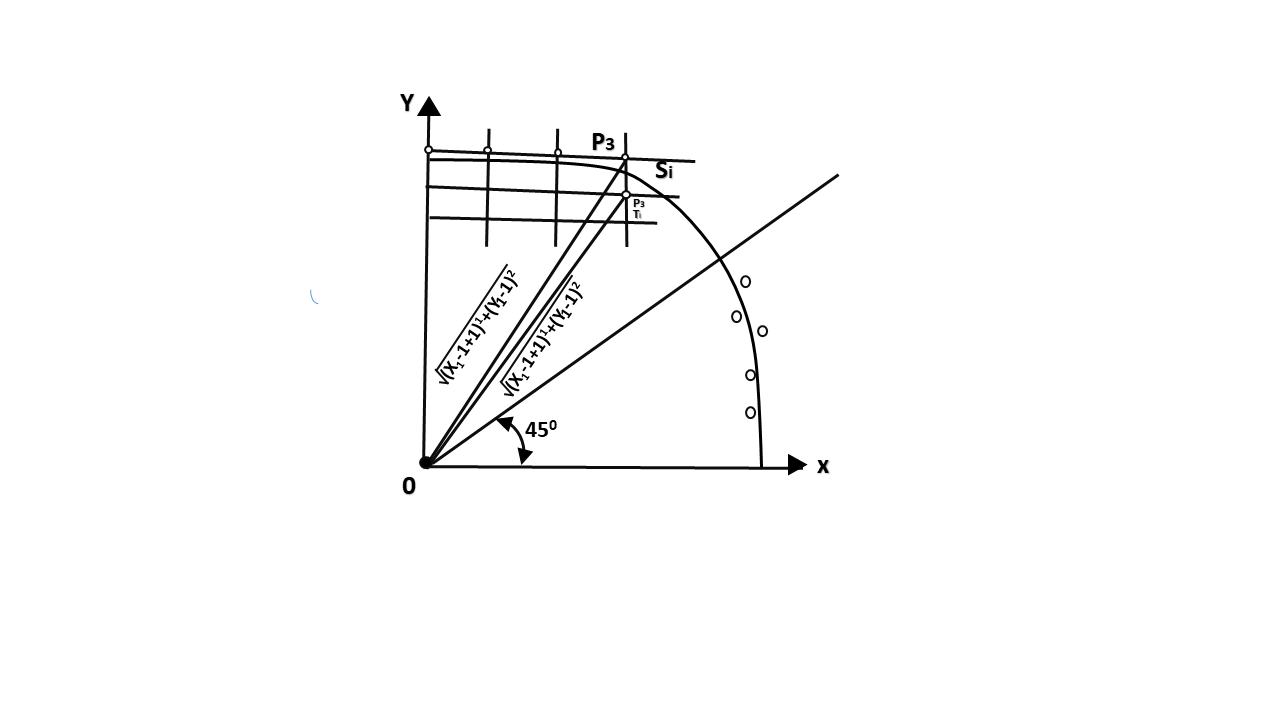
90°至45°。假定最后的经扫描转换的像素是P1, 如图2所示。可以通过以下两个动作之一找到最接近真实圆的每个新点。

1. 在x方向上移动一个单位或
2. 在x方向上移动一个单位, 在y方向上移动一个负数。

令D（Si）是从原点到真实圆平方的距离减去到点P3平方的距离。 D（Ti）是从原点到真圆平方的距离减去到点P2平方的距离。因此, 出现以下表达式。

D (Si)=(xi-1+1)2+ yi-12 -r2 D (Ti)=(xi-1+1)2+(yi-1 -1)2-r2

由于D（Si）始终为+ ve, 而D（Ti）始终为-ve, 因此可以将决策变量d定义如下：

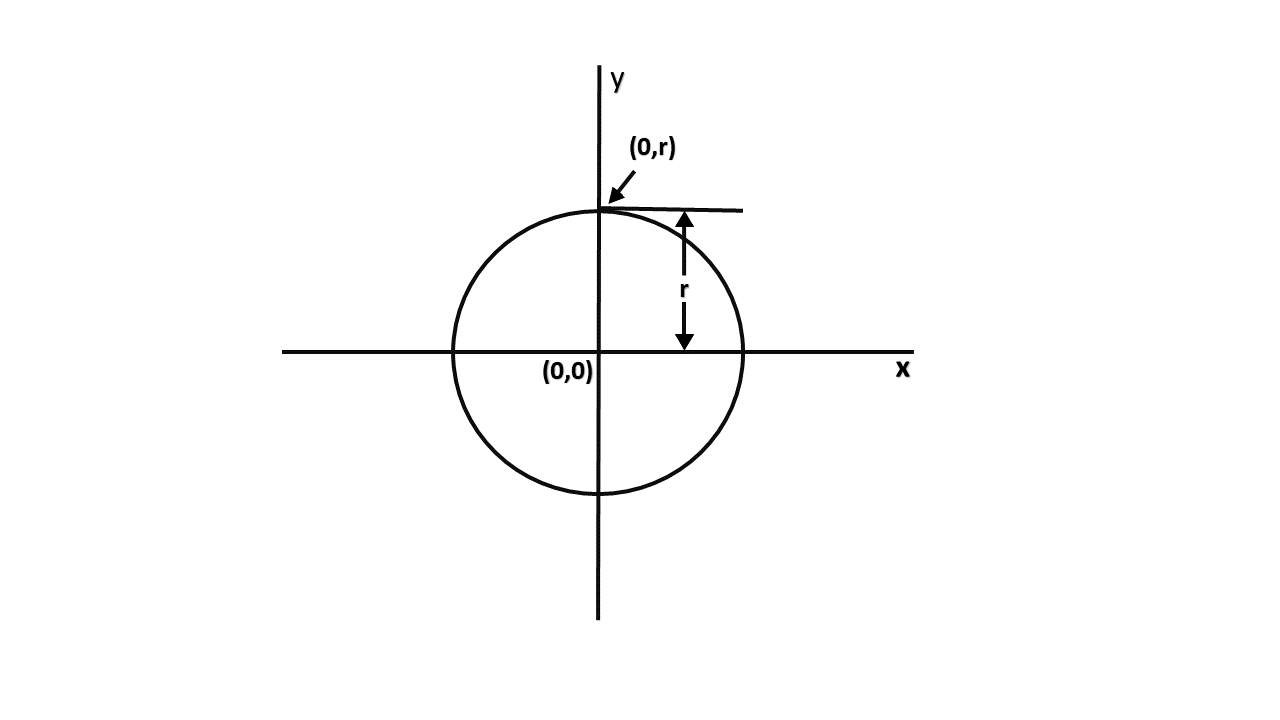
di = D（硅）+ D（Ti）

Therefore, di=(xi-1+1)2+ yi-12 -r2+(xi-1+1)2+(yi-1 -1)2-r2

从这个方程式, 我们可以将di的初始值驱动为

如果假定圆以原点为中心, 则第一步x = 0＆y = r。

因此, di =（0 + 1）2 + r2 -r2 +（0 + 1）2+（r-1）2-r2 = 1 + 1 + r2-2r + 1-r2 = 3-2r

此后, 如果d_i <0, 则仅x递增。

xi+1=xi+1 di+1=di+ 4xi+6

& if di≥0, then x & y are incremented xi+1=xi+1 yi+1 =yi+ 1 di+1=di+ 4 (xi-yi)+10

布雷森汉姆圆算法

步骤1：开始算法

步骤2：声明p, q, x, y, r, d变量p, q是圆心的坐标r是圆心的半径

步骤3：输入r的值

步骤4：计算d = 3-2r

步骤5：初始化x = 0＆nbsy = r

步骤6：检查整个圆是否已扫描转换如果x> = y停止

步骤7：使用八向对称的概念绘制八个点。中心位于（p, q）。当前有效像素为（x, y）。像素（x + p, y + q）像素（y + p, x + q）像素（-y + p, x + q）像素（-x + p, y + q）像素（-x + p, – y + q）像素（-y + p, -x + q）像素（y + p, -x + q）像素（x + p, -yq）

步骤8：查找要扫描的下一个像素的位置如果d <0, 则d = d + 4x + 6增量x = x + 1如果d≥0, 则d = d + 4（x-y）+ 10增量x = x + 1递减y = y-1

步骤9：前往步骤6

步骤10：停止算法

示例：使用Bresenham算法绘制6个圆点。圆弧半径为10个单位时。圆的中心为（50, 50）。

解决方案：令r = 10（给出）

步骤1：取初始点（0, 10）d = 3-2r d = 2-3 * 10 = -17 d <0 d = d + 4x + 6 = -17 + 4（0）+ 6 = -11

步骤2：绘制（1, 10）d = d + 4x + 6（∵d <0）= -11 + 4（1）+ 6 = -1

步骤3：绘制（2, 10）d = d + 4x + 6（∵d <0）= -1 + 4 x 2 + 6 = 13

第4步：绘制（3, 9）d> 0, 因此x = x + 1, y = y-1 d = d + 4（xy）+ 10（∵d> 0）= 13 + 4（3-9）+ 10 = 13 + 4（-6）+ 10 = 23-24 = -1

步骤5：绘制（4, 9）d = -1 + 4x + 6 = -1 + 4（4）+ 6 = 21

步骤6：绘制（5, 8）d = d + 4（x-y）+ 10（∵d> 0）= 21 + 4（5-8）+ 10 = 21-12 + 10 = 19

所以P1（0, 0）⟹（50, 50）P2（1, 10）⟹（51, 60）P3（2, 10）⟹（52, 60）P4（3, 9）⟹（53, 59）P5 （4, 9）⟹（54, 59）P6（5, 8）⟹（55, 58）

使用Bresenham的圆图绘制算法绘制圆的程序：

#include <graphics.h>
#include <stdlib.h>
#include <stdio.h>
#include <conio.h>
#include <math.h>

    void	EightWaySymmetricPlot(int xc, int yc, int x, int y)
   {
	putpixel(x+xc, y+yc, RED);
	putpixel(x+xc, -y+yc, YELLOW);
	putpixel(-x+xc, -y+yc, GREEN);
	putpixel(-x+xc, y+yc, YELLOW);
	putpixel(y+xc, x+yc, 12);
	putpixel(y+xc, -x+yc, 14);
	putpixel(-y+xc, -x+yc, 15);
	putpixel(-y+xc, x+yc, 6);
   }

    void BresenhamCircle(int xc, int yc, int r)
   {
	int x=0, y=r, d=3-(2*r);
	EightWaySymmetricPlot(xc, yc, x, y);

	while(x<=y)
     {
	  if(d<=0)
             {
	    d=d+(4*x)+6;
	  }
	 else
	  {
	    d=d+(4*x)-(4*y)+10;
	    y=y-1;
	  }
	   x=x+1;
	   EightWaySymmetricPlot(xc, yc, x, y);
      }
    }

    int  main(void)
   {
	/* request auto detection */
	int xc, yc, r, gdriver = DETECT, gmode, errorcode;
	/* initialize graphics and local variables */
	 initgraph(&gdriver, &gmode, "C:\\TURBOC3\\BGI");

	 /* read result of initialization */
	 errorcode = graphresult();

	  if (errorcode != grOk)  /* an error occurred */
	 {
		printf("Graphics error: %s\n", grapherrormsg(errorcode));
		printf("Press any key to halt:");
		getch();
		exit(1); /* terminate with an error code */
	 }
	   printf("Enter the values of xc and yc :");
	   scanf("%d%d", &xc, &yc);
	   printf("Enter the value of radius  :");
	   scanf("%d", &r);
	   BresenhamCircle(xc, yc, r);

	 getch();
	 closegraph();
	 return 0;
    }

输出：