它基于以下功能, 用于测试任意点(x, y)与以原点为中心的半径r的圆之间的空间关系:
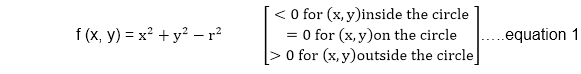
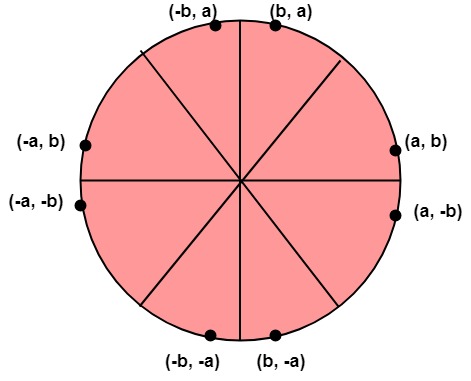
现在, 考虑像素T和像素S之间的中间点的坐标
这称为中点(xi + 1, yi-), 我们用它来定义决策参数:
Pi=f (xi+1, yi-) = (xi+1)2+(yi-)2-r2 ……………equation 2
如果Pi是-ve⟹中点在圆内, 我们选择像素T
如果Pi是+ ve⟹中点在圆之外(或在圆上), 我们选择像素S。
下一步的决策参数是:
Pi+1=(xi+1+1)2+(yi+1-)2- r2…………equation 3
由于xi + 1 = xi + 1, 我们有
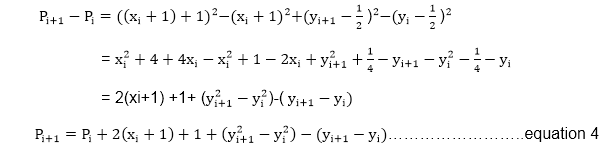
如果选择像素T⟹Pi<0
我们有yi + 1 = yi
如果选择像素S⟹Pi≥0
我们有yi + 1 = yi-1
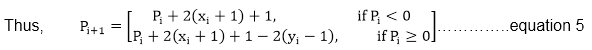
我们可以继续用(xi, yi)的n来简化它, 得到
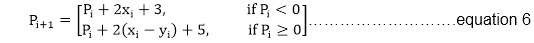
现在, 由等式2得出的Pi(0, r)的初始值
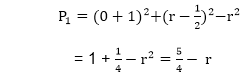
我们可以把≅1∴r是一个整数所以, P1 = 1-r
算法
步骤1:将x = 0, y = r代入等式2中, 我们有p = 1-r
步骤2:在x≤y的情况下重复步骤x(y, y)如果(p <0)然后设置p = p + 2x + 3其他p = p + 2(xy)+5 y = y-1(如果结束)x = x + 1(结束循环)
第三步:结束
程序使用中点算法绘制圆:
#include <graphics.h>
#include <stdlib.h>
#include <math.h>
#include <stdio.h>
#include <conio.h>
#include <iostream.h>
class bresen
{
float x, y, a, b, r, p;
public:
void get ();
void cal ();
};
void main ()
{
bresen b;
b.get ();
b.cal ();
getch ();
}
Void bresen :: get ()
{
cout<<"ENTER CENTER AND RADIUS";
cout<< "ENTER (a, b)";
cin>>a>>b;
cout<<"ENTER r";
cin>>r;
}
void bresen ::cal ()
{
/* request auto detection */
int gdriver = DETECT, gmode, errorcode;
int midx, midy, i;
/* initialize graphics and local variables */
initgraph (&gdriver, &gmode, " ");
/* read result of initialization */
errorcode = graphresult ();
if (errorcode ! = grOK) /*an error occurred */
{
printf("Graphics error: %s \n", grapherrormsg (errorcode);
printf ("Press any key to halt:");
getch ();
exit (1); /* terminate with an error code */
}
x=0;
y=r;
putpixel (a, b+r, RED);
putpixel (a, b-r, RED);
putpixel (a-r, b, RED);
putpixel (a+r, b, RED);
p=5/4)-r;
while (x<=y)
{
If (p<0)
p+= (4*x)+6;
else
{
p+=(2*(x-y))+5;
y--;
}
x++;
putpixel (a+x, b+y, RED);
putpixel (a-x, b+y, RED);
putpixel (a+x, b-y, RED);
putpixel (a+x, b-y, RED);
putpixel (a+x, b+y, RED);
putpixel (a+x, b-y, RED);
putpixel (a-x, b+y, RED);
putpixel (a-x, b-y, RED);
}
}输出:

 srcmini
srcmini
评论前必须登录!
注册