本文概述
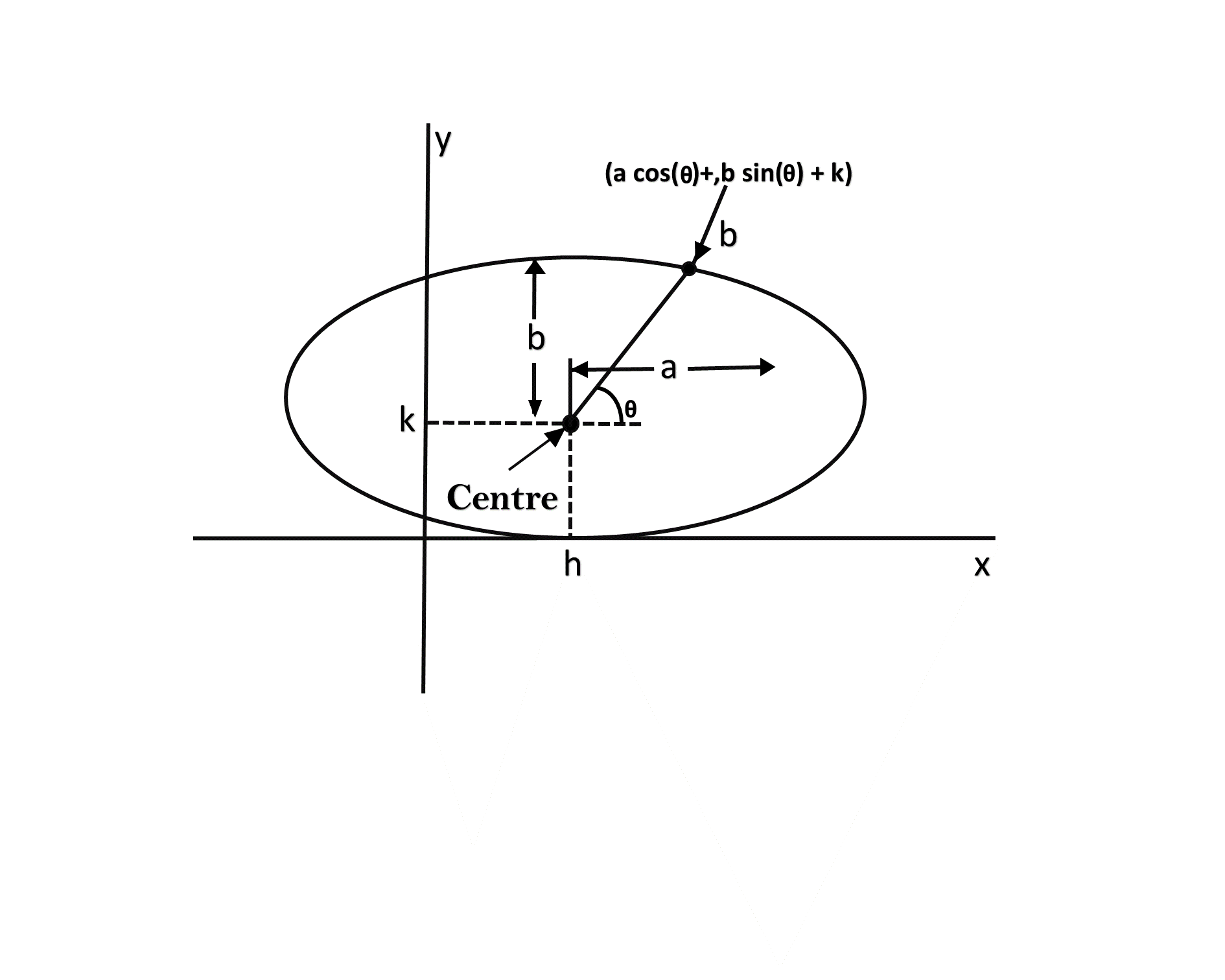
以下等式用三角函数定义了一个椭圆, 如图所示:
x = a * cos(θ)+ h, y = b * sin(θ)+ k其中(x, y)=当前坐标a =长轴长度b =短轴长度θ=当前角度(h, k)=椭圆中心
在此方法中, θ的值从0到弧度变化。其余点通过对称找到。
退税
- 这是一种低效的方法。
- 它不是用于生成椭圆的交互式方法。
- 需要该表才能查看三角值。
- 需要存储器来存储θ的值。
算法
步骤1:开始算法
步骤2:声明变量x1, y1, aa1, bb1, aa2, bb2, fx, fy, p1, a1, b1
步骤3:初始化x1 = 0和y1 = b / *圆起点的值* /
步骤4:计算aa1 = a1 * a1计算bb1 = b1 * b1计算aa2 = aa1 * 2计算bb2 = bb1 * 2
步骤5:初始化fx = 0
步骤6:初始化fy = aa_2 * b1
步骤7:计算p1的值, 如果它是整数p1 = bb1-aa1 * b1 + 0.25 * a1 /
步骤8:
While (fx < fy)
{
Set pixel (x1, y1)
Increment x i.e., x = x + 1
Calculate fx = fx + bb2
If (p1 < 0)
Calculate p1 = p1 + fx + bb1/
else
{
Decrement y i.e., y = y-1
Calculate fy = fy - 992;
p1=p1 + fx + bb1-fy
}
}步骤9:Setpixel(x1, y1)
步骤10:计算p1 = bb1(x + .5)(x + .5)+ aa(y-1)(y-1)-aa1 * bb1
步骤11:
While (y1>0)
{
Decrement y i.e., y = y-1
fy=fx-aa2/
if (p1>=0)
p1=p1 - fx + aa1/
else
{
Increment x i.e., x = x + 1
fx= fx+bb_2
p1=p1+fx-fy-aa1
}
}
Set pixel (x1, y1)步骤12:停止算法
程序使用三角法绘制圆:
#include <graphics.h>
#include <stdlib.h>
#include <math.h>
#include <stdio.h>
#include <conio.h>
#include <iostream.h>
# define pi 3.14
class bresen
{
float a, b, h, k, thetaend, step, x, y;
int i;
public:
void get ();
void cal ();
};
void main ()
{
bresen b;
b.get ();
b.cal ();
getch ();
}
void bresen :: get ()
{
cout<<"\n ENTER CENTER OF ELLIPSE";
cin>>h>>k;
cout<<"\n ENTER LENGTH OF MAJOR AND MINOR AXIS";
cin>>a>>b;
cout<<"\n ENTER STEP SIZE";
cin>> step;
}
void bresen ::cal ()
{
/* request auto detection */
int gdriver = DETECT, gmode, errorcode;
int midx, midy, i;
/* initialize graphics and local variables */
initgraph (&gdriver, &gmode, " ");
/* read result of initialization */
errorcode = graphresult ();
if (errorcode ! = grOK) /*an error occurred */
{
printf("Graphics error: %s \n", grapherrormsg (errorcode);
printf ("Press any key to halt:");
getch ();
exit (1); /* terminate with an error code */
}
theta= 0;
thetaend=(pi*90)/180;
whilex (theta<thetaend)
{
x = a * cos (theta);
y = b * sin (theta);
putpixel (x+h, y+k, RED);
putpixel (-x+h, y+k, RED);
putpixel (-x+h, -y+k, RED);
putpixel (x+h, -y+k, RED);
theta+=step;
}
getch();
}输出:
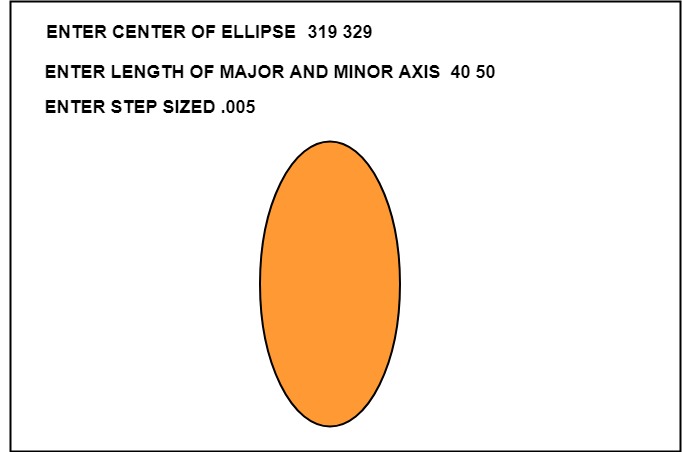
椭圆轴旋转
由于椭圆显示四向对称性, 因此可以轻松旋转。通过交换a和b(描述长轴和短轴的值)可以找到新的等式。当使用多项式方法时, 用于描述椭圆的方程变为
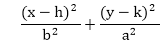
其中(h, k)=椭圆中心a =长轴长度b =短轴长度在三角法中, 方程为x = b cos(θ)+ h和y = a sin(θ)+ k
其中(x, y)=当前坐标a =主轴长度b =短轴长度θ=当前角度(h, k)=椭圆中心
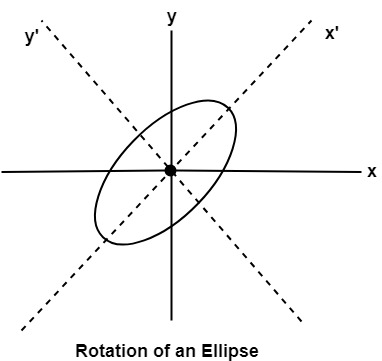
假设你想将椭圆旋转90度以外的角度。椭圆的旋转可以通过旋转x&y轴α度来实现。
x = a cos(0)-b sin(0+∞)+ h y = b(sin 0)+ a cos(0 +∞)+ k
 srcmini
srcmini
评论前必须登录!
注册