计算机图形：反射操作

这是一个转换, 生成对象的镜像。镜像可以是x轴或y轴。物体旋转180°。

反射类型

1. 关于x轴的思考
2. 关于y轴的思考
3. 围绕垂直于xy平面并通过原点的轴的反射
4. 关于线y = x的思考

1.关于x轴的反射：可以借助以下矩阵围绕x轴反射对象。

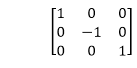
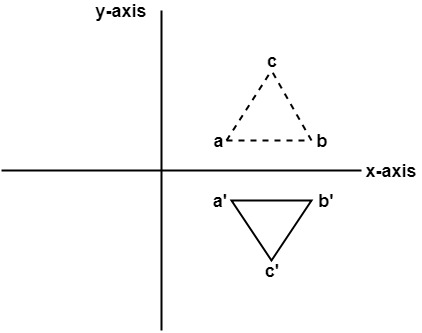
在此变换中, x的值将保持不变, 而y的值将变为负值。下图显示了对象轴的反射。该对象将位于x轴的另一侧。

2.关于y轴的反射：可以通过以下变换矩阵在y轴上反射对象。

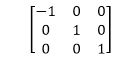
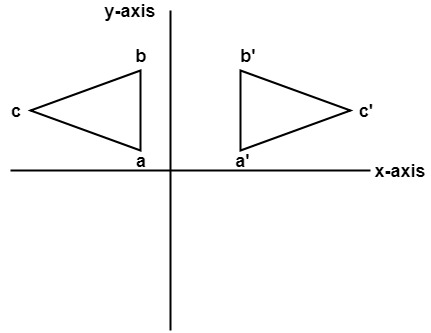
在这里x的值将被反转, 而y的值将保持不变。该对象将位于y轴的另一侧。

下图显示了关于y轴的反射

3.关于垂直于xy平面并经过原点的轴的反射：在此变换的矩阵中给出如下

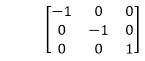
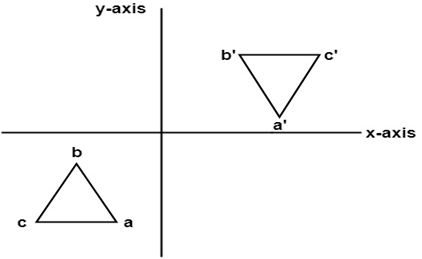
x和y的值都将相反。这也称为绕原点旋转半圈。

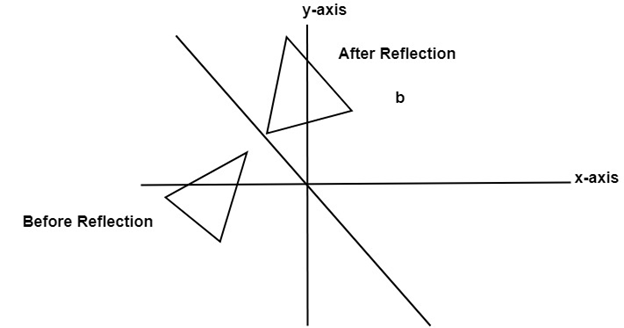
4.关于线y = x的反射：可以在以下变换矩阵的帮助下将对象绕线y = x反射

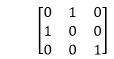
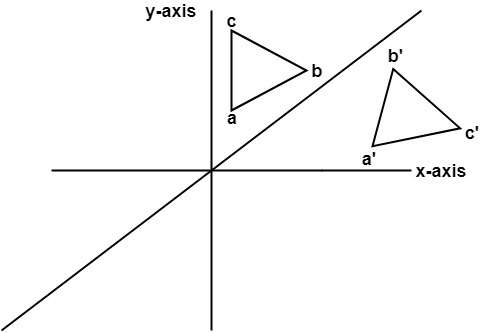
首先, 将对象旋转45°。旋转方向为顺时针方向。之后, 完成有关x轴的反射。最后一步是将y = x旋转回到其原始位置, 即逆时针旋转45°。

示例：给出一个三角形ABC。 A, B, C的坐标为

A（3 4）B（6 4）C（4 8）

找到三角形的反射位置, 即相对于x轴的位置。

解：

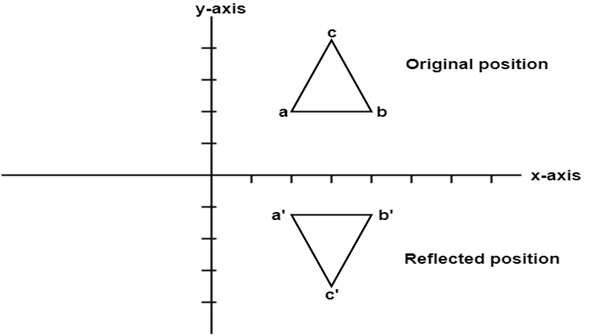
反射后的一个点坐标

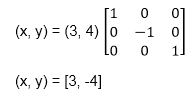
反射后的b点坐标

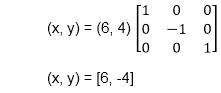
反射后c点的坐标

a（3, 4）变成a1（3, -4）b（6, 4）变成b1（6, -4）c（4, 8）变成c1（4, -8）

用于对一条线执行镜像反射的程序：

#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
#include <stdlib.h>
#define pi 3.14
class arc
{
	float x[10], y[10], theta, ref[10][10], ang;
           float p[10][10], p1[10][10], x1[10], y1[10], xm, ym;
	int i, k, j, n;
	public:
	void get();
	void cal ();
	void map ();
	void graph ();
	void plot ();
	void plot1();
};
void arc::get ()
{
	cout<<"\n ENTER ANGLE OF LINE INCLINATION AND Y INTERCEPT";
	cin>> ang >> b;
	cout <<"\n ENTER NO OF VERTICES";
	cin >> n;
	cout <<"\n ENTER";
	for (i=0; i<n; i++)
	{
		cout<<"\n x["<<i<<"] and y["<<i<<"]";
	}
	theta =(ang * pi)/ 180;
	ref [0] [0] = cos (2 * theta);
	ref [0] [1] = sin (2 * theta);
	ref [0] [2] = -b *sin (2 * theta);
	ref [1] [0] = sin (2 * theta);
	ref [1] [1] = -cos (2 * theta);
	ref [1] [2] = b * (cos (2 * theta)+1);
	ref [2] [0]=0;
	ref [2] [1]=0;
	ref [2] [2] = 1;
}
void arc :: cal ()
{
	for (i=0; i < n; i++)
	{
		p[0] [i] = x [i];
		p [1] [i] = y [i];
		p [2] [i] = 1;
	}
	for (i=0; i<3;i++)
	{
		for (j=0; j<n; j++)
		{
			p1 [i] [j]=0;
			for (k=0;k<3; k++)
		}
		p1 [i] [j] + = ref [i] [k] * p [k] [j];
             }
for (i=0; i<n; i++)
   {
	x1 [i]=p1[0] [i];
	y1 [i] = p1 [1] [i];
    }
}
void arc :: map ()
{
	int gd = DETECT, gm;
	initgraph (&gd, &gm, " ");
            int errorcode = graphresult ();
	/* an error occurred */
	if (errorcode ! = grOK)    
	{
 		printf ("Graphics error: %s \n", grapherrormsg (errorcode));
		printf ("Press any key to halt:");
		getch ();
		exit (1); /* terminate with an error code */
	}
}
void arc :: graph ()
{
	xm=getmaxx ()/2;
	ym=getmaxy ()/2;
	line (xm, 0, xmm 2*ym);
}
void arc :: plot 1 ()
{
	for (i=0; i <n-1; i++)
	{
		circle (x1[i]+xm, (-y1[i]+ym), 2);
		line (x1[i]+xm, (-y1[i]+ym), x1[i+1]+xm, (-y1[i+1]+ym));
	}
		line (x1[n-1)+xm, (-y1[n-1]+ym), x1[0]+xm, (-y1[0]+ym));
		getch();
}
void arc :: plot ()
{ 
	for (i=0; i <n-1; i++)
	{
		circle (x1[i]+xm, (-y1[i]+ym, 2);
		line (x1[i]+xm, (-y1[i]+ym), x[i+1]+xm, (-y1[i+1]+ym));
	}
		line (x[n-1]+xm, (-y1[n-1]+ym), x[0]+xm, (-y[0]+ym));
		getch();
}
void main ()
{
	class arc a;
	clrscr();
	a.map();
	a.graph();
	a.get();
	a.cal();
	a.plot();
	a.plot1();
	getch();
}

输出：