解码器可以描述为一种组合电路, 它将二进制信息从“ n”个编码输入转换为最多2 ^ n个不同的输出。
注意:n位的二进制代码能够表示多达2 ^ n个编码信息的不同元素。
最优选或常用的解码器是n-m解码器, 其中m <= 2 ^ n。
n-m解码器具有n个输入和m个输出, 也称为n * m解码器。
下图显示了具有3个输入变量的3至8行解码器, 这些输入变量被解码为8个输出, 每个输出代表三个二进制输入变量的组合之一。
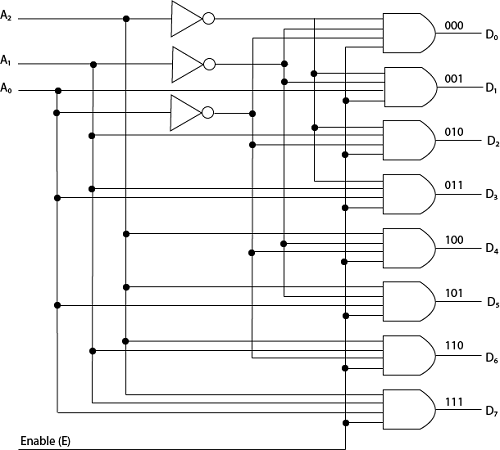
三个反相器门提供输入的补码, 与之对应的是输出端的八个与门为每个输入生成一个二进制组合。
该解码器最常见的应用是二进制到八进制的转换。
3到8行解码器的真值表可以表示为:
| X | 和 | 从 | D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
让我们考虑一个2到4行NAND门解码器的示例, 该解码器在中央逻辑中使用NAND门而非AND门。
下图显示了具有NAND门的2至4行解码器。
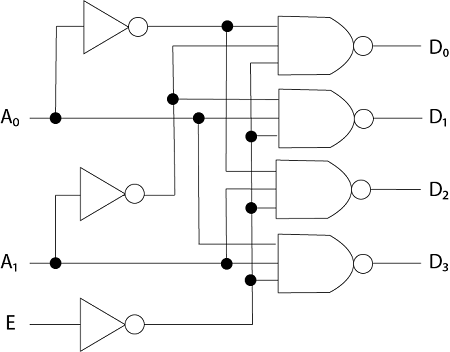
2至4行解码器的真值表可以表示为:
| 和 | A1 | A0 | D0 | D1 | D2 | D3 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
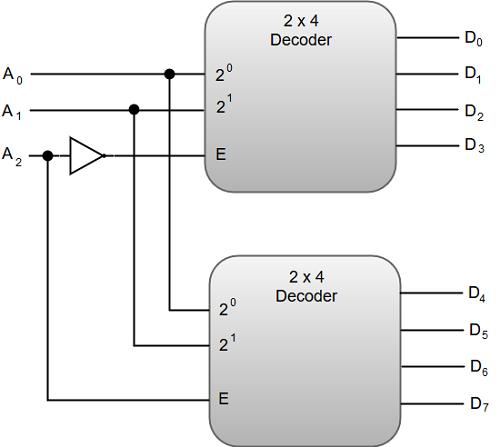
每当需要时, 也可以组合两个或多个解码器以形成大型解码器。例如, 我们可以通过组合两个2 * 4解码器来构造3 * 8解码器。
下图显示了由两个2 * 4解码器构成的3 * 8解码器。
 srcmini
srcmini
评论前必须登录!
注册