本文概述
任何系统都可以用一组微分方程来描述, 或者可以用包含所有组件及其连接的示意图来表示。但是, 这些方法不适用于复杂的系统。
框图表示是这两种方法的组合。方框图表示使用方框的系统。
为了使用框图表示任何系统, 必须找到系统的传递函数, 即输出拉普拉斯与输入拉普拉斯的比率。

哪里
R(s) = Input
C(s) = output
G(s) = transfer function然后, 系统可以表示为
C(s) = R(s).G(s)求和点:当我们想将不同的输入信号应用于同一块时, 所得的输入信号就是所有输入的总和。输入信号的总和由称为求和点的交叉圆表示, 如下图所示。
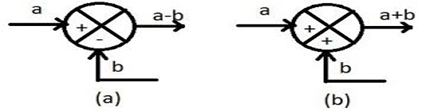
起飞点:如果有多个块, 并且我们希望将相同的输入应用于所有块, 则使用起飞点。通过使用起飞点, 相同的输入将传播到所有块, 而不会影响其值。下图显示了同一输入到多个块的表示。
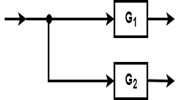
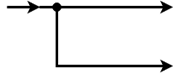
如何绘制框图
考虑一个简单的R-L电路
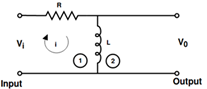
申请KVL
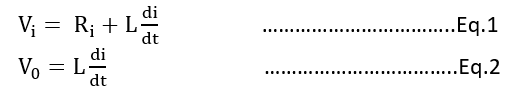
现在对初始条件为零的等式1和等式2进行拉普拉斯变换

从等式3和等式4
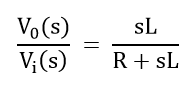
从图:

现在进行等式5和等式6的拉普拉斯变换
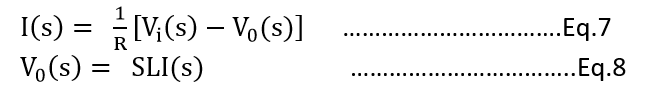
对于等式5的右侧, 我们将使用一个求和点。
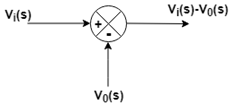
此处, 求和点的输出提供给该块, 该块的输出为I(s)
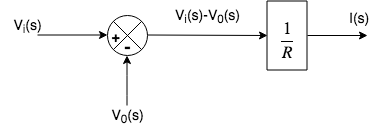
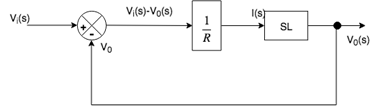
现在, 将输出I(s)提供给包含元素SL的另一个块, 并且该块的输出为V0。

通过结合以上两个图, 我们获得了所需的框图。
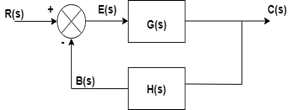
闭环控制系统
其中存在反馈路径的系统称为闭环控制系统。在此系统中, 输出被反馈到错误检测器, 然后将其与输入信号进行比较。反馈信号可以为负或正。
获得积极的反馈
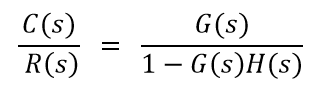
并获得负面反馈
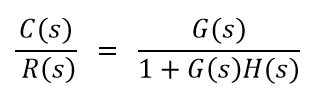
框图减少规则
规则一级联中的块
当两个或多个块串联时, 则所得块为各个块的乘积。

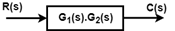
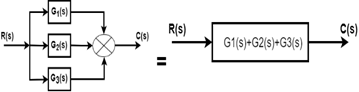
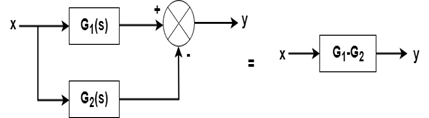
规则2并行块
当两个或多个块并联连接时, 结果块为各个块之和。
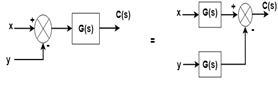
规则3:将起飞点移至方块前
当起飞点移动到一个程序段之前(该程序段之前)时, 则在起飞点分支中引入了相同的传递函数。

规则4:将起飞点移至方块后
当起飞点在程序段之后移动时, 则在起飞点分支中引入一个具有传递函数倒数的程序段。

规则5:将求和点移出程序段
规则6:将求和点移动到块的前面
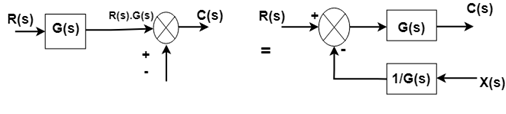
规则7:交换两个求和点
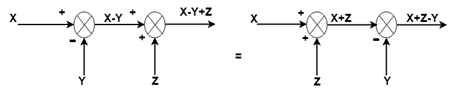
规则8:将起飞点移到加和点之外
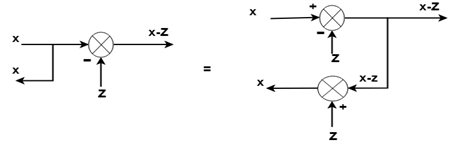
规则9:将起飞点移到求和点之前
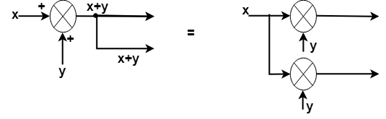
规则10:消除前向循环
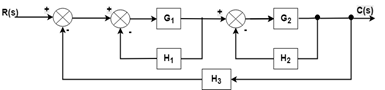
例
通过块减少技术找到以下的传递函数。
解
步骤1:有两个内部闭环。首先, 我们将删除此循环。
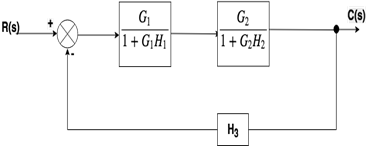
第2步:当两个模块串联或串联时, 我们将使用规则1。
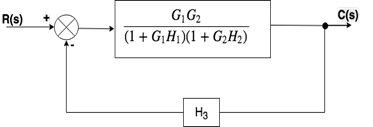
步骤3:现在我们将解决此循环。
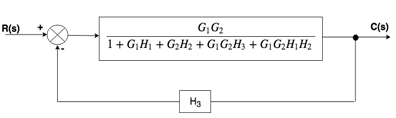
步骤4:
 srcmini
srcmini
评论前必须登录!
注册