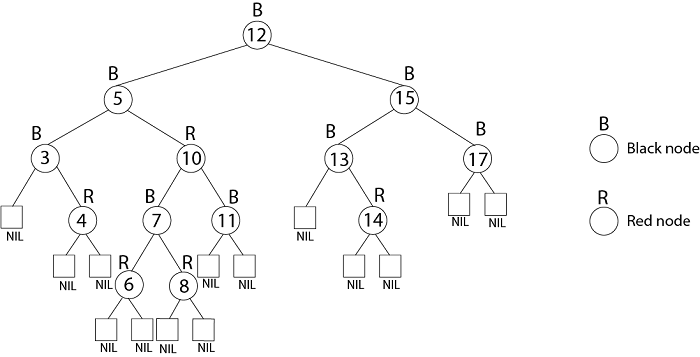
本文概述
红黑树是自平衡二进制搜索树的类别。它是由鲁道夫·拜耳(Rudolf Bayer)于1972年创建的, 他称其为“对称二叉B树”。
红黑树是二叉树, 其中特定节点具有颜色作为额外属性, 无论是红色还是黑色。通过检查从根到叶的任何简单路径上的节点颜色, 红黑树确保该路径的长度不超过其他任何路径的两倍, 因此树通常是平衡的。
红黑树的性质
红黑树必须满足以下属性:
- 根始终是黑色的。
- 零被识别为黑色。每个非NIL节点都有两个子节点的原因。
- 黑子规则:任何红色节点的子都是黑。
- 黑色高度规则:对于特定的节点v, 存在整数bh(v), 这样从v到nil的特定向下路径正确地具有bh(v)黑色实数(即非nil)节点。将此部分称为v的黑色高度。我们将RB树的黑色高度确定为其根的黑色高度。
如果树的根是红色, 则树T几乎是一棵红黑树(ARB树), 但上述其他条件成立。
RB树上的操作
搜索树操作TREE-INSERT和TREE-DELETE在带有n个键的红黑树上运行时, 花费O(log n)时间。因为他们自定义树, 所以结论可能违反了红黑色属性。要恢复这些属性, 我们必须更改树中某些节点的颜色, 并更改指针结构。
1.轮播:
红黑树上的重组操作通常可以在旋转操作的细节中更清楚地表达。
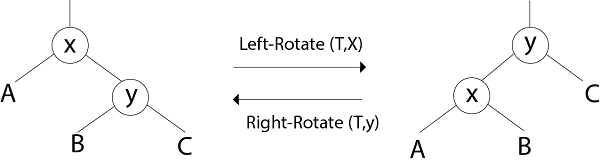
显然, 旋转操作会保留顺序(Ax C)。因此, 如果我们从BST开始并且仅使用旋转进行重组, 那么我们仍将拥有BST, 即旋转不会破坏BST属性。
LEFT ROTATE (T, x)
1. y ← right [x]
1. y ← right [x]
2. right [x] ← left [y]
3. p [left[y]] ← x
4. p[y] ← p[x]
5. If p[x] = nil [T]
then root [T] ← y
else if x = left [p[x]]
then left [p[x]] ← y
else right [p[x]] ← y
6. left [y] ← x.
7. p [x] ← y.示例:在键{1, 2, 3 … 15}上绘制高度为3的完整二叉树。添加NIL叶子并以三种不同的方式为节点着色, 以使生成的树的黑色高度为:2、3和4。
解:
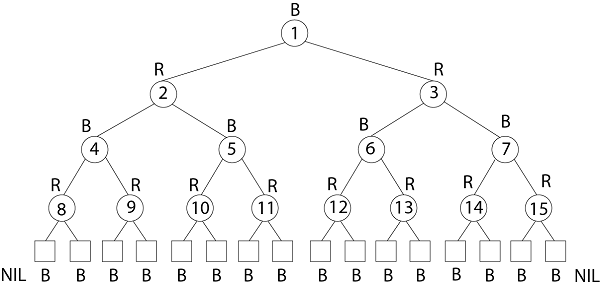
黑高2树
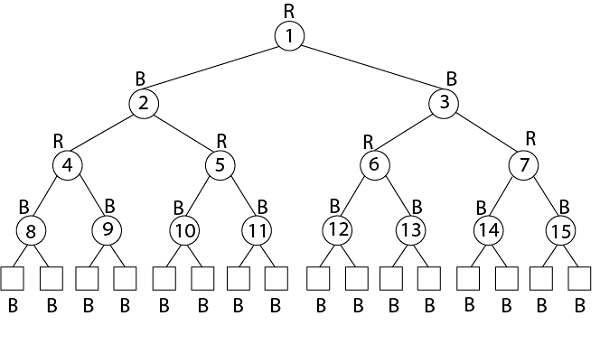
黑高3树
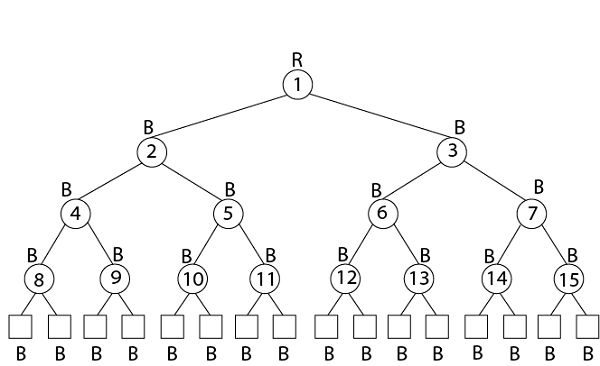
黑高4树
2.插入:
- 按照在二进制搜索树中完成操作的方式插入新节点。
- 将节点涂成红色
- 如果红黑树发生不一致, 请根据差异类型修复树。
差异可以由父母和孩子都具有红色的决定来决定。这种类型的差异取决于与祖父母有关的节点的位置以及父级的同级的颜色。
RB-INSERT (T, z)
1. y ← nil [T]
2. x ← root [T]
3. while x ≠ NIL [T]
4. do y ← x
5. if key [z] < key [x]
6. then x ← left [x]
7. else x ← right [x]
8. p [z] ← y
9. if y = nil [T]
10. then root [T] ← z
11. else if key [z] < key [y]
12. then left [y] ← z
13. else right [y] ← z
14. left [z] ← nil [T]
15. right [z] ← nil [T]
16. color [z] ← RED
17. RB-INSERT-FIXUP (T, z)在插入新节点之后, 将此新节点着色为黑色可能会违反黑色高度条件, 而将此新节点着色为红色可能会违反着色条件, 即根为黑色, 红色节点没有红色子节点。我们知道违反黑高度的规定很难。因此, 我们将节点涂成红色。此后, 如果有任何颜色冲突, 那么我们必须通过RB-INSERT-FIXUP过程进行纠正。
RB-INSERT-FIXUP (T, z)
1. while color [p[z]] = RED
2. do if p [z] = left [p[p[z]]]
3. then y ← right [p[p[z]]]
4. If color [y] = RED
5. then color [p[z]] ← BLACK //Case 1
6. color [y] ← BLACK //Case 1
7. color [p[z]] ← RED //Case 1
8. z ← p[p[z]] //Case 1
9. else if z= right [p[z]]
10. then z ← p [z] //Case 2
11. LEFT-ROTATE (T, z) //Case 2
12. color [p[z]] ← BLACK //Case 3
13. color [p [p[z]]] ← RED //Case 3
14. RIGHT-ROTATE (T, p [p[z]]) //Case 3
15. else (same as then clause)
With "right" and "left" exchanged
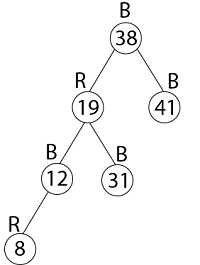
16. color [root[T]] ← BLACK示例:显示在将键41、38、31、12、19、8依次插入最初为空的红黑树之后生成的红黑树。
解:
插入41
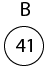
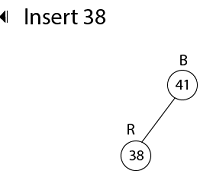
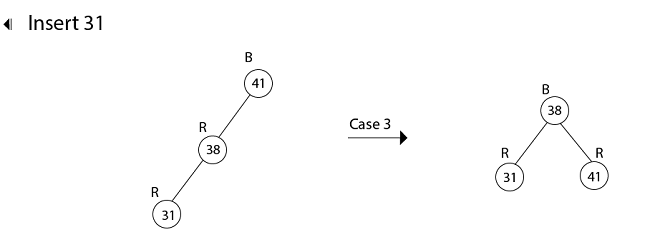
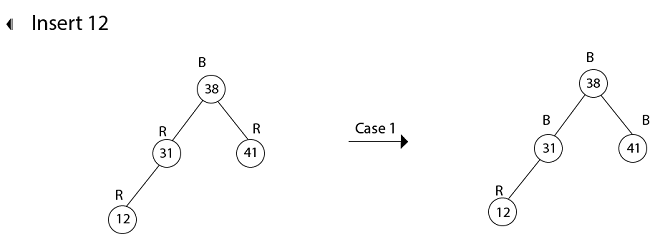
插入19
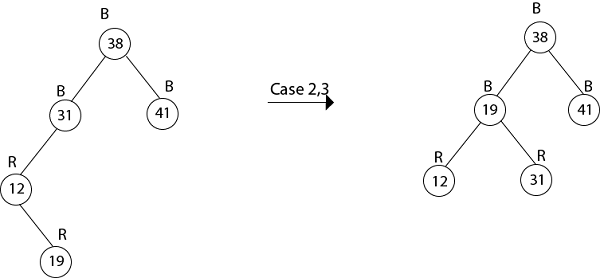
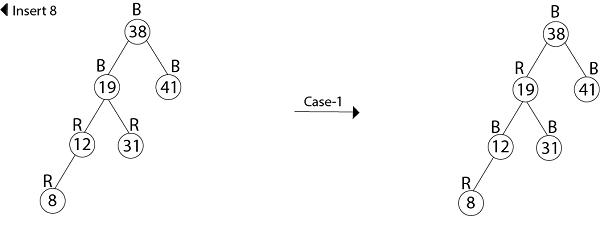
因此, 最后一棵树是
3.删除:
首先, 搜索要删除的元素
- 如果要删除的元素位于只有左子节点的节点中, 请将该节点与包含左子树中最大元素的节点交换。 (此节点没有合适的孩子)。
- 如果要删除的元素在只有右子节点的节点中, 请将该节点与包含右子树中最小元素的节点交换(该节点没有左子节点)。
- 如果要删除的元素在具有左子节点和右子节点的节点中, 则可以通过以上两种方式中的任何一种进行交换。交换时, 仅交换键, 而不交换颜色。
- 现在, 要删除的项目只有一个左孩子或只有一个右孩子。将此节点替换为其唯一的子节点。这可能违反红色约束或黑色约束。违反红色约束的问题很容易解决。
- 如果删除的节点为黑色, 则违反黑色约束。消除黑色节点y会导致包含y的任何路径的黑色节点减少一个。
- 出现两种情况:替换节点为红色, 在这种情况下, 我们仅将其着色为黑色, 以弥补一个黑色节点的损失。替换节点为黑色。
策略RB-DELETE是对TREE-DELETE程序的微小更改。拼接节点后, 它会调用辅助过程RB-DELETE-FIXUP, 该过程会更改颜色并执行旋转以恢复红黑色属性。
RB-DELETE (T, z)
1. if left [z] = nil [T] or right [z] = nil [T]
2. then y ← z
3. else y ← TREE-SUCCESSOR (z)
4. if left [y] ≠ nil [T]
5. then x ← left [y]
6. else x ← right [y]
7. p [x] ← p [y]
8. if p[y] = nil [T]
9. then root [T] ← x
10. else if y = left [p[y]]
11. then left [p[y]] ← x
12. else right [p[y]] ← x
13. if y≠ z
14. then key [z] ← key [y]
15. copy y's satellite data into z
16. if color [y] = BLACK
17. then RB-delete-FIXUP (T, x)
18. return yRB-DELETE-FIXUP (T, x)
1. while x ≠ root [T] and color [x] = BLACK
2. do if x = left [p[x]]
3. then w ← right [p[x]]
4. if color [w] = RED
5. then color [w] ← BLACK //Case 1
6. color [p[x]] ← RED //Case 1
7. LEFT-ROTATE (T, p [x]) //Case 1
8. w ← right [p[x]] //Case 1
9. If color [left [w]] = BLACK and color [right[w]] = BLACK
10. then color [w] ← RED //Case 2
11. x ← p[x] //Case 2
12. else if color [right [w]] = BLACK
13. then color [left[w]] ← BLACK //Case 3
14. color [w] ← RED //Case 3
15. RIGHT-ROTATE (T, w) //Case 3
16. w ← right [p[x]] //Case 3
17. color [w] ← color [p[x]] //Case 4
18. color p[x] ← BLACK //Case 4
19. color [right [w]] ← BLACK //Case 4
20. LEFT-ROTATE (T, p [x]) //Case 4
21. x ← root [T] //Case 4
22. else (same as then clause with "right" and "left" exchanged)
23. color [x] ← BLACK示例:在前面的示例中, 我们发现了红黑树是由于将键41、38、31、12、19、8依次插入到最初为空的树中而产生的。现在显示成功删除键顺序为8、12、19、31、38、41的红黑树。
解:
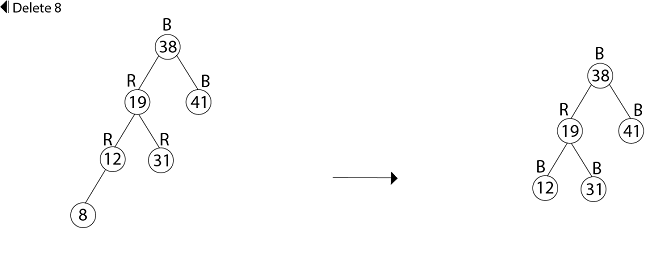
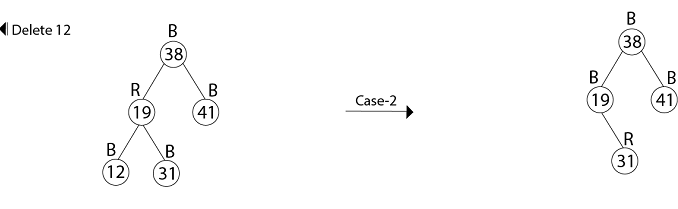
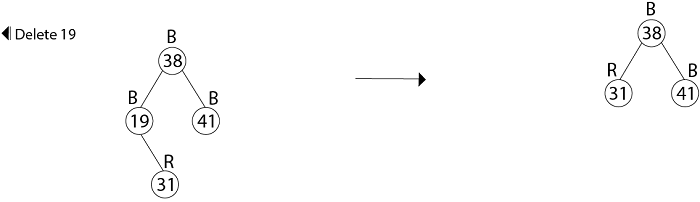

删除38
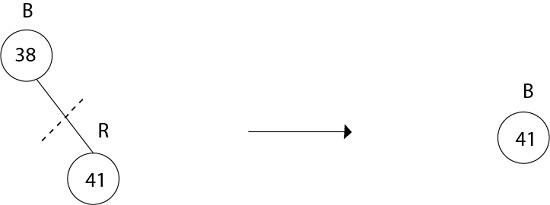
删除41
没有树。
 srcmini
srcmini
评论前必须登录!
注册