本文概述
Robert Boyer和J Strother Moore于1977年成立了它。B-M字符串搜索算法是一种特别有效的算法, 自那时以来一直作为字符串搜索算法的标准基准。
B-M算法采用“后退”方法:将模式字符串(P)与文本字符串(T)的开头对齐, 然后从最右边的字符开始, 从右至左比较模式的字符。
如果比较的字符不在模式中, 则无法通过分析此位置上的任何其他方面找到匹配项, 因此可以完全通过不匹配字符更改模式。
为了确定可能的偏移, B-M算法同时使用了两种预处理策略。每当发生不匹配时, 如果每种情况都使用最有效的策略, 则该算法会使用两种方法来计算偏差并选择更为显着的偏移。
这两种策略被称为B-M的启发式算法, 因为它们用于减少搜索。他们是:
- 错误字符启发法
- 良好的后缀启发式
1.坏字符启发法
这种启发式方法有两个含义:
- 假设文本中根本没有字符出现在模式中。当此字符发生不匹配(称为坏字符)时, 可以更改整个模式, 开始匹配此“坏字符”旁边的表单子字符串。
- 另一方面, 模式中可能存在错误字符, 在这种情况下, 请将模式的性质与文本中的错误字符对齐。
因此, 在任何情况下, 偏移都可能大于一个。
示例1:让文本T = <nyoo nyoo>和模式P = <noyo>
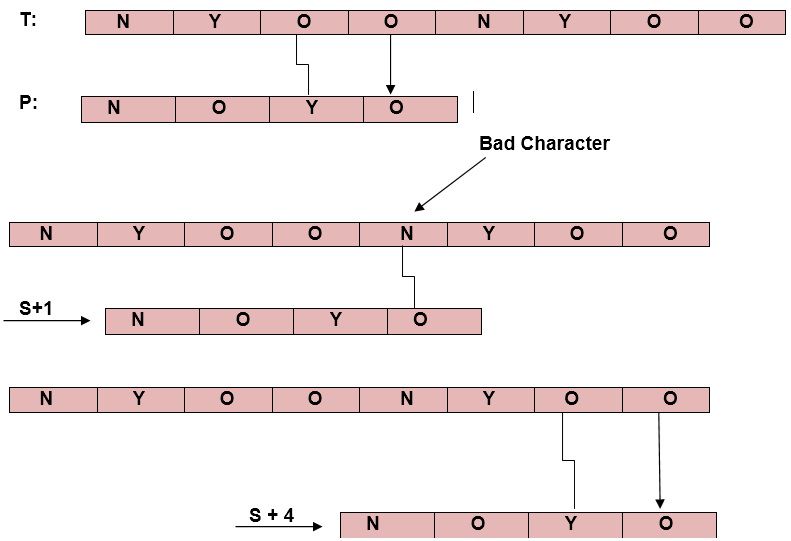
例2:如果不存在错误字符, 则模式。
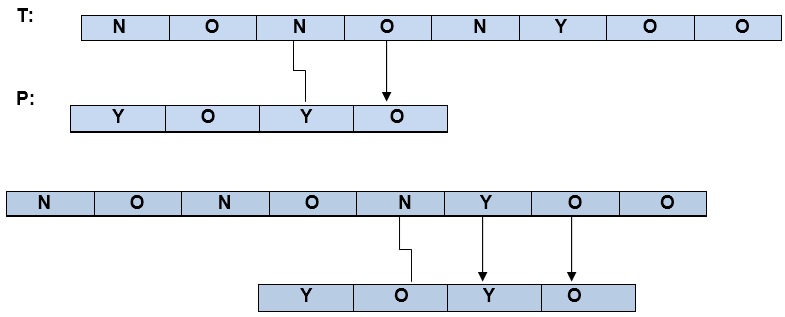
坏字符启发法中的问题:
在某些情况下, 坏字符启发法会产生一些负面变化。
例如:
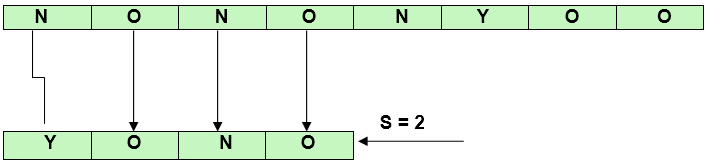
这意味着我们需要一些额外的信息, 以便在遇到不良角色时产生转变。该信息与模式中每个方面的最后位置有关, 也与模式中使用的字符集(通常称为模式的字母∑)有关。
COMPUTE-LAST-OCCURRENCE-FUNCTION (P, m, ∑ )
1. for each character a ∈ ∑
2. do λ [a] = 0
3. for j ← 1 to m
4. do λ [P [j]] ← j
5. Return λ2.良好的后缀启发式
良好的后缀是成功匹配的后缀。在不匹配之后, 不良字符启发法将发生负向偏移, 请查看是否匹配的模式子串直到不良字符中具有良好的后缀为止, 如果是这样, 则我们向前跳转的长度等于找到的后缀的长度。
例:
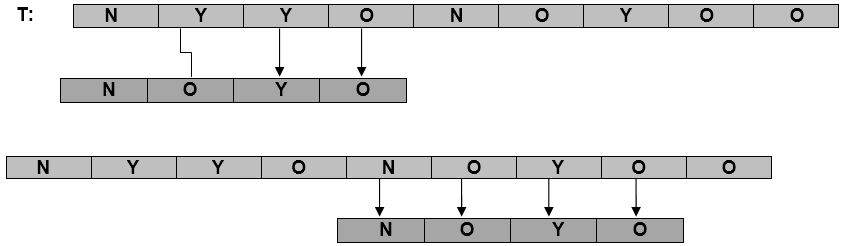
COMPUTE-GOOD-SUFFIX-FUNCTION (P, m)
1. Π ← COMPUTE-PREFIX-FUNCTION (P)
2. P'← reverse (P)
3. Π'← COMPUTE-PREFIX-FUNCTION (P')
4. for j ← 0 to m
5. do ɣ [j] ← m - Π [m]
6. for l ← 1 to m
7. do j ← m - Π' [L]
8. If ɣ [j] > l - Π' [L]
9. then ɣ [j] ← 1 - Π'[L]
10. Return ɣBOYER-MOORE-MATCHER (T, P, ∑)
1. n ←length [T]
2. m ←length [P]
3. λ← COMPUTE-LAST-OCCURRENCE-FUNCTION (P, m, ∑ )
4. ɣ← COMPUTE-GOOD-SUFFIX-FUNCTION (P, m)
5. s ←0
6. While s ≤ n - m
7. do j ← m
8. While j > 0 and P [j] = T [s + j]
9. do j ←j-1
10. If j = 0
11. then print "Pattern occurs at shift" s
12. s ← s + ɣ[0]
13. else s ← s + max (ɣ [j], j - λ[T[s+j]])字符串匹配算法的复杂度比较:
| 算法 | 预处理时间 | 比赛时间 |
|---|---|---|
| Naive | O | (O(n-m +1)m) |
| Rabin-Karp | O(m) | (O(n-m +1)m) |
| Finite Automata | O(m|∑|) | O (n) |
| Knuth-Morris-Pratt | O(m) | O (n) |
| Boyer-Moore | O(|∑|) | (O((n-m + 1)+ | ∑ |)) |
 srcmini
srcmini
评论前必须登录!
注册