本文概述
AVL树由GM Adelson-Velsky和EM Landis于1962年发明。为了纪念其发明者, 该树被命名为AVL。
AVL树可以定义为高度平衡的二叉搜索树, 其中每个节点都与一个平衡因子相关联, 该平衡因子是通过从其左子树的高度中减去其右子树的高度来计算的。
如果每个节点的平衡因子在-1到1之间, 则认为树是平衡的, 否则, 树将不平衡, 需要平衡。
平衡系数(k)=高度(left(k))-高度(right(k))
如果任何节点的平衡因子为1, 则表示左子树比右子树高一级。
如果任何节点的平衡因子为0, 则表示左子树和右子树的高度相等。
如果任何节点的平衡因子为-1, 则表示左子树比右子树低一级。
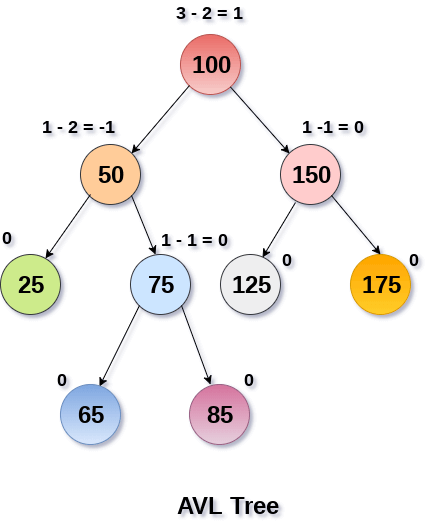
下图给出了一个AVL树。我们可以看到, 与每个节点关联的平衡因子在-1和+1之间。因此, 它是AVL树的一个示例。
复杂
| 算法 | 平均情况 | 最差的情况 |
|---|---|---|
| Space | o(n) | o(n) |
| Search | o(log n) | o(log n) |
| Insert | o(log n) | o(log n) |
| Delete | o(log n) | o(log n) |
在AVL树上的操作
由于AVL树也是二叉搜索树, 因此, 所有操作的执行方式与二叉搜索树中执行操作的方式相同。搜索和遍历不会导致违反AVL树的属性。但是, 插入和删除是可能违反此属性的操作, 因此, 需要重新研究它们。
| 序号 | 运作方式 | 描述 |
|---|---|---|
| 1 | Insertion | 以与在二叉搜索树中执行的相同方式执行在AVL树中的插入。但是, 这可能会导致违反AVL树属性, 因此可能需要平衡该树。可以通过应用旋转来平衡树。 |
| 2 | Deletion | 删除也可以与在二叉搜索树中执行的相同方式执行。删除还可能会干扰树的平衡, 因此, 使用各种类型的旋转来重新平衡树。 |
为什么选择AVL树?
AVL树通过不使其偏斜来控制二进制搜索树的高度。在高度为h的二叉搜索树中, 所有操作所需的时间为O(h)。但是, 如果BST偏斜(即最坏的情况), 则可以将其扩展为O(n)。通过将此高度限制为log n, AVL树将每个操作的上限设置为O(log n), 其中n是节点数。
 srcmini
srcmini
评论前必须登录!
注册