本文概述
二进制搜索是一种在排序列表上有效工作的搜索技术。因此, 为了使用二进制搜索技术将元素搜索到某个列表中, 我们必须确保对列表进行排序。
二进制搜索遵循分而治之的方法, 其中将列表分为两半, 并将项目与列表的中间元素进行比较。如果找到匹配项, 则返回中间元素的位置, 否则, 我们将根据通过匹配项产生的结果搜索这两个部分。
二元搜索算法如下。
BINARY_SEARCH(A, Lower_bound, upper_bound, VAL)
- 步骤1:[INITIALIZE] SET BEG = lower_bound END = upper_bound, POS =-1
- 步骤2:在BEG <= END的同时重复步骤3和4
- 步骤3:SET MID =(BEG + END)/ 2
- 步骤4:如果A [MID] = VAL SET POS = MID PRINT POS转到步骤6 ELSE如果A [MID]> VAL SET END = MID-1 ELSE SET BEG = MID + 1 [IF的结束] [LOOP结束]
- 步骤5:如果POS = -1, 则打印“阵列中不存在值” [IF结束]
- 步骤6:退出
复杂
| 序号 | 性能 | 复杂 |
|---|---|---|
| 1 | Worst case | O(log n) |
| 2 | 最好的情况 | O(1) |
| 3 | Average Case | O(log n) |
| 4 | 最坏情况下的空间复杂度 | O(1) |
例
让我们考虑一个数组arr = {1、5、7、8、13、19、20、23、29}。在数组中找到项目23的位置。
第一步:
BEG = 0
END = 8ron
MID = 4
a[mid] = a[4] = 13 < 23, therefore在第二步:
Beg = mid +1 = 5
End = 8
mid = 13/2 = 6
a[mid] = a[6] = 20 < 23, therefore;第三步:
beg = mid + 1 = 7
End = 8
mid = 15/2 = 7
a[mid] = a[7]
a[7] = 23 = item;
therefore, set location = mid;
The location of the item will be 7.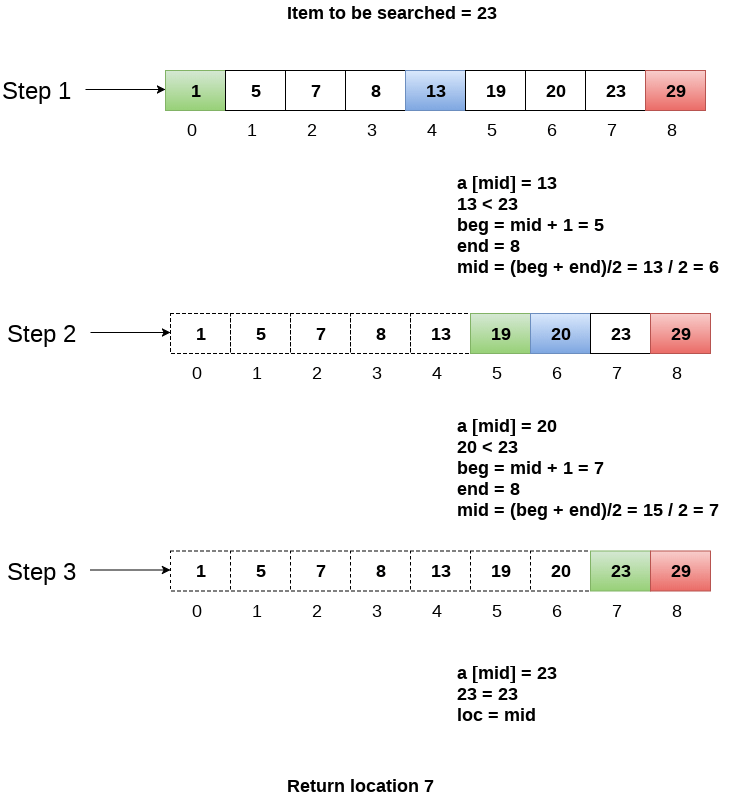
使用递归的二进制搜索程序
C程序
#include<stdio.h>
int binarySearch(int[], int, int, int);
void main ()
{
int arr[10] = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
int item, location=-1;
printf("Enter the item which you want to search ");
scanf("%d", &item);
location = binarySearch(arr, 0, 9, item);
if(location != -1)
{
printf("Item found at location %d", location);
}
else
{
printf("Item not found");
}
}
int binarySearch(int a[], int beg, int end, int item)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == item)
{
return mid+1;
}
else if(a[mid] < item)
{
return binarySearch(a, mid+1, end, item);
}
else
{
return binarySearch(a, beg, mid-1, item);
}
}
return -1;
}输出:
Enter the item which you want to search
19
Item found at location 2爪哇
import java.util.*;
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
int item, location = -1;
System.out.println("Enter the item which you want to search");
Scanner sc = new Scanner(System.in);
item = sc.nextInt();
location = binarySearch(arr, 0, 9, item);
if(location != -1)
System.out.println("the location of the item is "+location);
else
System.out.println("Item not found");
}
public static int binarySearch(int[] a, int beg, int end, int item)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == item)
{
return mid+1;
}
else if(a[mid] < item)
{
return binarySearch(a, mid+1, end, item);
}
else
{
return binarySearch(a, beg, mid-1, item);
}
}
return -1;
}
}输出:
Enter the item which you want to search
45
the location of the item is 5C#
using System;
public class LinearSearch
{
public static void Main()
{
int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
int location=-1;
Console.WriteLine("Enter the item which you want to search ");
int item = Convert.ToInt32(Console.ReadLine());
location = binarySearch(arr, 0, 9, item);
if(location != -1)
{
Console.WriteLine("Item found at location "+ location);
}
else
{
Console.WriteLine("Item not found");
}
}
public static int binarySearch(int[] a, int beg, int end, int item)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == item)
{
return mid+1;
}
else if(a[mid] < item)
{
return binarySearch(a, mid+1, end, item);
}
else
{
return binarySearch(a, beg, mid-1, item);
}
}
return -1;
}
}输出:
Enter the item which you want to search
20
Item found at location 3蟒蛇
def binarySearch(arr, beg, end, item):
if end >= beg:
mid = int((beg+end)/2)
if arr[mid] == item :
return mid+1
elif arr[mid] < item :
return binarySearch(arr, mid+1, end, item)
else:
return binarySearch(arr, beg, mid-1, item)
return -1
arr=[16, 19, 20, 23, 45, 56, 78, 90, 96, 100];
item = int(input("Enter the item which you want to search ?"))
location = -1;
location = binarySearch(arr, 0, 9, item);
if location != -1:
print("Item found at location %d" %(location))
else:
print("Item not found")输出:
Enter the item which you want to search ?
96
Item found at location 9
Enter the item which you want to search ?
101
Item not found使用迭代的二进制搜索功能
int binarySearch(int a[], int beg, int end, int item)
{
int mid;
while(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == item)
{
return mid+1;
}
else if(a[mid] < item)
{
beg = mid + 1;
}
else
{
end = mid - 1;
}
}
return -1;
} srcmini
srcmini
评论前必须登录!
注册