数据挖掘贝叶斯分类器

在许多应用程序中, 属性集和类变量之间的连接是不确定的。换句话说, 即使测试记录的类标签的属性集与某些训练示例的属性集相同, 也可以肯定地说它不能被假定为类标签。这些情况可能是由于嘈杂的数据或某些影响分类的混乱因素而出现的, 但未包括在分析中。例如, 考虑根据个人的饮食习惯和工作效率来预测个人是否有患肝病的风险的任务。尽管大多数健康饮食和持续运动的人发生肝脏疾病的可能性较小, 但由于其他因素, 他们仍然可能这样做。例如, 由于食用了高热量的街头食品和酗酒。确定一个人的饮食习惯是否健康或锻炼效率是否足够还需要进行分析, 这反过来可能会将脆弱性引入到易感性问题中。

贝叶斯分类使用贝叶斯定理来预测任何事件的发生。贝叶斯分类器是具有贝叶斯概率理解的统计分类器。该理论表示信念水平如何以概率表示。

贝叶斯定理在托马斯·贝叶斯之后诞生, 他首先利用条件概率来提供一种算法, 该算法使用证据来计算未知参数的极限。

贝叶斯定理由下面给出的下列方程式数学表示。

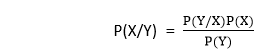
其中X和Y是事件, P（Y）≠0

P（X / Y）是描述事件X发生的条件概率, 假设Y为真。

P（Y / X）是描述X成立的事件Y发生的条件概率。

P（X）和P（Y）是彼此独立观察X和Y的概率。这称为边际概率。

贝叶斯解释：

在贝叶斯解释中, 概率确定“信念度”。贝叶斯定理在说明证据之前和之后将假设的信念程度联系起来。例如, 让我们考虑一个硬币的例子。如果我们抛硬币, 那么正面或反面都会出现, 正面和反面出现的百分比是50％。如果硬币被翻转了几次, 并且观察到结果, 则信念程度可能会上升, 下降或保持不变, 这取决于结果。

对于命题X和证据Y,

• 先验P（X）是对X的主要信任程度
• P（X / Y）, 后验是占Y的置信度。
• 商表示Y为X提供的支持。

贝叶斯定理可以从条件概率中得出：

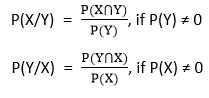
其中P（X⋂Y）是X和Y均为真的联合概率, 因为

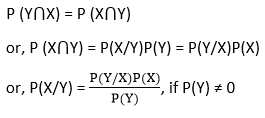
贝叶斯网络：

贝叶斯网络属于概率图形建模（PGM）程序的类别, 该程序通过利用概率概念来计算不确定性。贝叶斯网络通常称为Belief网络, 用于通过有向无环图（DAG）显示不确定性

有向无环图用于显示贝叶斯网络, 和其他统计图一样, DAG由一组节点和链接组成, 其中链接表示节点之间的连接。

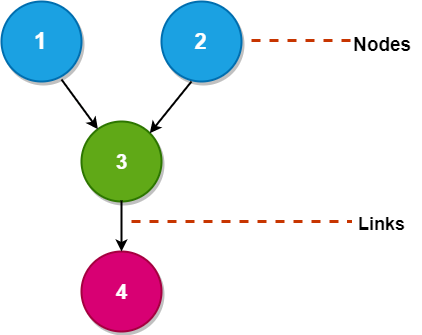
此处的节点表示随机变量, 边缘定义这些变量之间的关系。

DAG根据每个随机变量的条件概率分布（CDP）对事件的不确定性进行建模。条件概率表（CPT）用于表示网络中每个变量的CPD。