本文概述
在数学分析中, 算法的渐近分析是定义其运行时性能的数学界限的一种方法。使用渐近分析, 我们可以轻松得出算法的平均情况, 最佳情况和最坏情况。
它用于数学计算算法内部任何操作的运行时间。
示例:一个操作的运行时间为x(n), 而另一操作的运行时间计算为f(n2)。它指的是第一次运行的运行时间将随着“ n”的增加而线性增加, 而第二次运行的运行时间将呈指数增长。同样, 如果n很小, 则两个操作的运行时间将相同。
通常, 算法所需的时间分为以下三种类型:
最坏的情况:它定义了算法需要花费大量时间的输入。
平均情况:程序平均花费时间。
最佳情况:它定义算法所需时间最少的输入。
渐近符号
下面给出了用于计算算法运行时间复杂度的常用渐近符号:
- 大O符号(Ο)
- 欧米茄(Z)
- θ符号(θ)
大O记法(O)
这是表达算法运行时间上限的正式方法。它可以测量算法完成工作所需的最复杂的时间复杂度或最长的时间。表示如下:
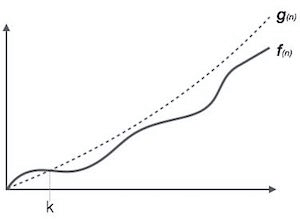
例如:如果f(n)和g(n)是为正整数定义的两个函数, 则f(n)为O(g(n)), 因为f(n)大于g(n)或f如果存在常数c并且不存在这样的常数, 则(n)的阶数为g(n)):
对于所有n≥no的F(n)≤cg(n)
这意味着f(n)的增长不会快于g(n), 或者g(n)是函数f(n)的上限。
欧米茄(Z)
这是表示算法运行时间下限的正式方法。它测量算法完成可能花费的最佳时间或最佳情况下的时间复杂度。
如果我们要求算法至少花费一定的时间而不使用上限, 则使用大Ω表示法, 即希腊字母“ omega”。它用于限制大输入量时运行时间的增长。
如果运行时间为Ω(f(n)), 则对于较大的n值, 对于常数(k), 运行时间至少为k?f(n)。表示如下:
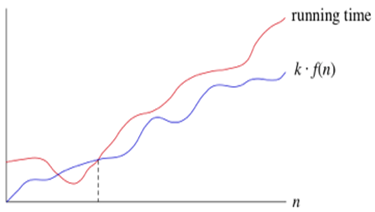
Theta表示法(?)
这是表达算法运行时间的上限和下限的正式方法。
考虑算法的运行时间为θ(n), 如果一次(n)足够大, 则对于某些常数k1和k2, 运行时间最多为k2-n, 至少为k1?n。表示如下:
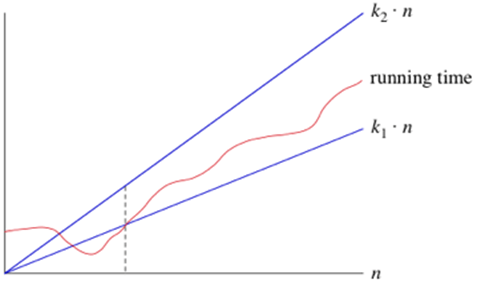
常见渐近符号
| constant | – | ?(1) |
| linear | – | ?(n) |
| logarithmic | – | ?(log n) |
| n日志n | – | ?(n log n) |
| exponential | – | 2?(n) |
| cubic | – | ?(n3) |
| polynomial | – | n?(1) |
| quadratic | – | ?(n2) |
 srcmini
srcmini
评论前必须登录!
注册