本文概述
可以将图形定义为一组顶点和用于连接这些顶点的边。图可以看作是循环树, 其中顶点(节点)在它们之间保持任何复杂的关系, 而不是具有父子关系。
定义
可以将图G定义为有序集合G(V, E), 其中V(G)代表顶点集合, E(G)代表用于连接这些顶点的边集合。
具有5个顶点(A, B, C, D, E)和六个边线((A, B), (B, C), (C, E), (E, D)的图G(V, E), (D, B), (D, A))如下图所示。

有向图和无向图
图可以是有向的或无向的。但是, 在无向图中, 边不与它们的方向相关联。上图中显示了无向图, 因为其边缘未附着任何方向。如果在顶点A和B之间存在边, 则可以从B到A以及从A到B遍历顶点。
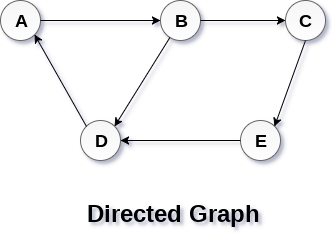
在有向图中, 边形成有序对。边表示从某个顶点A到另一个顶点B的特定路径。节点A称为初始节点, 而节点B称为终端节点。
下图显示了有向图。
图术语
路径
路径可以定义为为了从初始节点U到达某个终端节点V而遵循的节点序列。
封闭路径
如果初始节点与终端节点相同, 则将路径称为封闭路径。如果V0 = VN, 则路径为封闭路径。
简单路径
如果图的所有节点都不同(例外V0 = VN), 则将这种路径P称为封闭简单路径。
周期
循环可以定义为除了第一个和最后一个顶点外没有重复的边或顶点的路径。
连接图
连通图是V中每两个顶点(u, v)之间存在某种路径的连通图。连通图中没有孤立的节点。
完整图
一个完整的图是其中每个节点都与所有其他节点连接的图。一个完整的图包含n(n-1)/ 2条边, 其中n是图中的节点数。
加权图
在加权图中, 每个边都分配有一些数据, 例如长度或权重。边缘e的权重可以表示为w(e), 它必须是表示穿越边缘的成本的正(+)值。
有向图
有向图是有向图, 其中图的每个边都与某个方向相关联, 并且只能在指定方向上进行遍历。
环
与相似端点关联的边可以称为“循环”。
相邻节点
如果两个节点u和v通过边e连接, 则节点u和v被称为邻居或相邻节点。
节点度
节点的度数是与该节点连接的边数。度为0的节点称为隔离节点。
 srcmini
srcmini
评论前必须登录!
注册