在上一节我们谈到二叉树、AVL平衡二叉树、伸展树、B-树和B+树原理,相对于树,散列表(Hash Table)或哈希表无疑是一种相当适合使用在快速内存访问上的一种数据结构。树的理想时间复杂度可达到O(logn),而散列表理想情况下可达到常数的执行时间O(1)。但是散列表不支持排序,也不支持查找最大最小元素,因而在不需要考虑排序的情况下,我们可以利用散列表获得更快的执行效率。
散列表或哈希表是一种相当好的数据结构,在一般语言中都有实现,例如Java中的Set和Map、Python中的字典dict和Object-C中的字典NSDictionary。和数组相比,数组的寻址比较容易,插入和删除困难(最差为O(n)),而链表寻址困难(O(n)),插入和删除比较容易,散列表除了不支持排序,散列表寻址容易,同时插入和删除也容易。散列表有以下特点:
- 访问速度快,最快为O(1);
- 需要额外空间,散列表需要更多的空间来避免散列冲突或聚集;
- 无序,散列表不能实现元素排序;
- 可能产生碰撞,散列碰撞会影响散列表的执行效率。
除了一般的数据结构的应用,散列表还广泛用于数字摘要,也就是文件或数据加密,包括密码加密,字符串匹配算法如Rabin-Karp算法,编译器的实现,以及文件系统中的文件名和文件路径等,散列表的高级应用在数据持久化或数据缓存如redis或memcached。下面我们详细介绍散列表的实现原理,散列表定义、散列函数的几种实现方式、散列表的几种实现方式以及散列表的相关应用,并提供相关的实例代码。

一、散列表的概念和定义(Concepts And Definitions Of Hash Table)
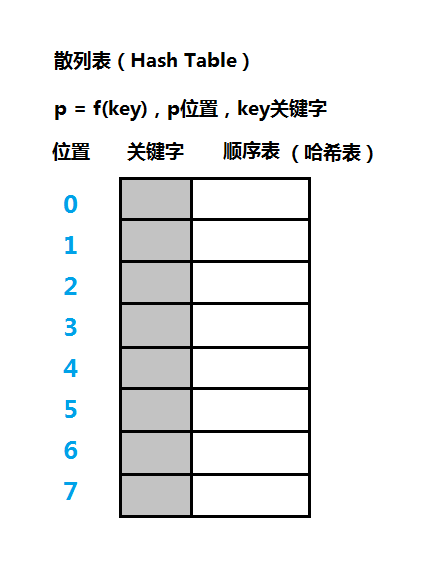
散列表是一种使用空间换取时间的数据结构,可以以常数的时间插入和查找记录。那么什么是哈希表或散列表?散列表其实就是一个顺序表或数组,假设散列表的每个单元存储一个记录(Record),在该记录中取一个成员作为关键字(Key),和关键字相对应的另一部分是记录的值(Value),每个记录在表中都有对应的索引位置(Position),如上图。
那么散列表有什么不同呢?找一个函数f,该函数的输入参数为key,输出为position,也就是说通过key即可计算记录的所在的索引位置,这个函数又称为散列函数或哈希函数,计算得出的位置值又称为散列地址,所以在散列表这种数据结构中,我们可以简单地通过关键字key操作数据记录。
1、散列函数(Hash Function)
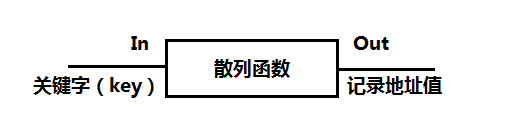
散列函数或哈希函数的主要作用是将关键字转为一个记录的整数地址值,经过散列函数映射后,若得到的是随机地址则是最理想的。但是有可能不同关键字会映射到同一地址上,即f(key1)=f(key2)=value,这种散列冲突情况的关键字又称为同义词。
散列表中的关键字和散列函数理论上可以任意指定,对于关键字的计算,一般关键字有两种情况,数字和字符串,假设表大小为size,对于整数可以通过p=key%size计算得到散列地址,注意,这里最好保证size为素数或质数,或取不大于散列表大小的质数,否则会影响散列表的效率。
关键字的另一种情况是字符串,对于是字符串的关键字,我们可以简单地将每个字符的ASCII码加起来,然后对size取模,或者是,h=0为散列地址,将h左移动5位再和字符的ASCII码相加。
由上面的内容,我们可以看到,散列表主要讨论两个内容:散列函数的实现和散列冲突的解决办法或散列表的实现。
2、装填因子(Load Factor)
设m为表的大小,n为关键字数或记录数,则a=n/m为散列表的装填因子,a是散列表装满程度的标志因子,假设表长m不变,a越大填入表中的元素越多,容纳更多的元素,但是造成冲突的机会越大;a越小散列表越稀疏,对空间的利用率越低,但是造成冲突的机会越小。
对于下面会介绍的解决散列冲突的方法或散列表的实现方式中,装填因子可用于分辨出该方式的效率是否好,例如对于分离链接法或拉链法装填因子a接近1的效率最好,对于开放寻址法,装填因子a不大于1,或者取0.75会比较好。
二、散列函数的实现(Implementations Of Hash Function)
上面提到,散列函数理论上是可以任意指定的,而下面讨论的散列函数的构造方法只是一些常见的方式,一般来说是足够用的了,但是还是要根据实际情况使用。另外,这里讨论的散列函数都是假设函数的输入为数字,换为字符串也是合适的,关键是这个字符串是如何转为数字,一般来说叠加各个字符的ASCII码,这其中还可以加入一些复杂的运算以达到要求,例如在字符串匹配算法Rabin-Karp算法中,可取各字符的ASCII码乘以10的n次方,然后叠加,再进行处理。
注意下面会给出相应的代码实现,还没有实际的散列表的完整代码,因为只讨论散列函数,如果你有需要,可以简单实现一个散列表,和数组或顺序表没什么区别。
1、直接定址法
改构造法取关键字或关键字的某个线性函数为散列值,如f(k)或f(k)=a*k+b,a和b为常数。因为是线性函数,所以该方式散列分布比较均匀,不会产生冲突,但是要求关键字有合适的分布情况,虽然该方法简单,但是并不常用,下面是该方式的代码:
int hash_direct_addr(int key){
return 2*key + 1;
}
2、数字分析法
如果关键字的若干位分布比较均匀,而另外的部分分布不均匀,那么可以取该关键字的若干位作为散列地址。一般来说可以去除关键字中相似的部分,取不同的部分合并为散列值,该方法在一些场合使用是比较方便的,例如学生的学号、身份证或手机号码,但是有可能引起冲突。这里以手机号码为例子,手机号码的后四位为用户号,号码一般为11位,代码如下:
// 2、数字分析法
int hash_digit_analyze(const char *key, int len){
if(key == NULL || len < 0)
return -1;
char number[4];
int j = 3;
for (int i = len - 1; i > len - 5; --i) {
number[j] = key[i];
j--;
}
return strtol(number, NULL, 10);
}
3、相乘取整法
首先确定常数A(0 < A < 1),然后取出key*A的小数部分,最后m和该小数部分相乘取整,得到散列地址,在这里表长m的选取不限于素数,这里建议选取2的整数次幂,A也可以任意选取,但建议选取黄金分割系数,即A=(根号5-1)/2,约为0.618033988……,实现代码如下:
// 3、相乘取整法
int hash_mutiply(int key){
float a = 0.618;
int m = 16;
float count = a * key;
return (int)(m * (count - (int)count));
}
4、平方取中法
当关键字差别很大,但是位数不是很多时,可以使用平方取中法,取关键字平方后的中间几位为散列地址,若表长m是一个b位数,那么取中间的b-1位,实现代码如下:
// 4、平方取中法
int hash_square(int key){
int m = 100, b = 3;
int value = key * key;
char str[32];
sprintf(str, "%d", value);
int index = (strlen(str) - b - 1) / 2;
char number[b - 1];
int j = 0;
for (int i = index; i < index + b - 1; ++i) {
number[j] = str[i];
j++;
}
return strtol(number, NULL, 10);
}
5、折叠法
当关键字位数比较多的时候可以使用折叠法,折叠法将关键字分隔成几部分,然后将这几部分分别叠加求和,若表长m为b位数,则按b位分隔关键字,取总和的后b位为散列地址,实现代码如下:
// 5、折叠法
int hash_fold(int key){
int m = 100, b = 3;
char str[32];
sprintf(str, "%d", key);
int count = 0, len = strlen(str);
for (int i = 0; i < len; i += b) {
int temp = 0;
for (int j = 0; j < b && i + j < len; ++j) {
temp = (int)(temp + pow(str[i + j] - 48, b - j));
}
count += temp;
}
char value[32];
sprintf(value, "%d", count);
int l = strlen(value);
if(l <= b)
return count;
int hash = 0;
for (int k = 0; k < b; ++k) {
hash = (int)(hash + pow(str[l - 1 - k] - 48, k + 1));
}
return hash;
}
6、随机数散列法
当关键字长度不等时,使用随机数法是较好的方法,选择一个随机函数,取关键字的随机函数值作为它的散列地址,实现代码如下:
// 6、随机数散列法
static unsigned int randseed = 1103515245;
int hash_rand(int key){
int m = 100;
unsigned int r;
r = randseed = key * randseed + 12345;
return ((r << 16) | ((r >> 16) & 0xFFFF)) % m;
}
7、取余散列法
该散列法是最重要也是最简单的散列法,一般情形都可以使用该方式实现一个散列函数,其它的散列函数构造法可结合该方式进行使用,取余散列法为:f(key)=key%m,实现代码如下:
// 7、取余散列法
int hash_mod(int key){
int m = 20;
return key % m;
}
8、平方散列法
平方散列法的散列函数为:f(key)=(key*key)>>28,该算法有可能算出全部都是0,并不是很理想,实现代码如下:
// 8、平方散列法
int hash_sq(int key){
return (key * key) >> 28;
}
9、斐波那契散列法
该方法的散列函数为:f(k)=(k*u)>>28,u的取值为:16位整数,u=40503,32位整数u=2654435769,64位整数u= 11400714819323198485,实现代码如下:
// 9、斐波那契散列法
int hash_fibo(int key){
return (key * 2654435769) >> 28;
}
在实际开发中,选择一个散列函数需要考虑以下几种情况:
- 散列函数的执行时间;
- 关键字的长度;
- 关键字的分布情况;
- 散列表的长度;
- 查找记录的频率。
散列函数的完整代码github项目:https://github.com/onnple/hashfunction,若有任何问题欢迎指正。
三、散列表的实现(散列冲突处理)(Collision Handling)
首先实现一个散列表,最基本的数据结构为数组或顺序表,在构造散列表的时候,表长m尽量选取素数,然后需要选择一个较好的散列函数,因为这个散列函数并不尽完美,所以我们现在要处理散列表发生冲突的情况。下面介绍的每种处理散列冲突的方式,每种方式有其对散列表实现的不同方式,例如分离链接法需要链表,而开放寻址法则无需其它数据结构单独在表上处理,可扩散列则是类似树的数据结构。
在以下散列表的实现中,会提供相应的实现代码,这些实例代码散列表对应的经典实际应用,除了可扩散列外,其它的实现方式一般不会太难,由于散列表比较重要而常用,建议动手操作更好掌握好散列表。
1、分离链接法(Separate Chaining)
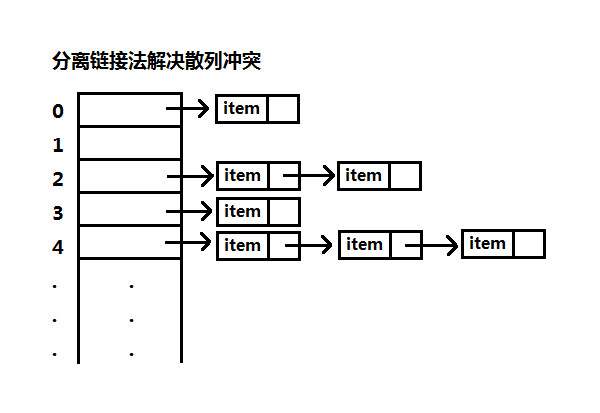
分离链接法使用链表来解决散列冲突,当有不同关键字映射到同一位置时,将该关键字插入到该关键字的一个链表上。也就是说分离链接法的散列表其实就是一个链表数组,可将数组中的项留空作为表头,当然这会浪费一些空间。
装填因子a=n/m,m为表长,n为关键字数或记录数,分离链接法的搜索期望时间为O(1+a),插入或删除期望时间为O(1+a),当a接近O(1)时,搜索、插入、删除的时间复杂度为O(1),所以分离链接法在装填因子a接近1时的性能最好。
使用分离链接法实现散列表时,首先我们要构建一个数组链表,链表的表头可留空(可选项),其中插入数据在表头插入,其它操作一般比较简单。
这里使用分离链接法散列表实现一个集合HashMap,类似其它语言的Set和Map,Set的key和value是一样的,Map和key和value不需要一样,其中一些语言也称为字典dict,下面是HashMap的ADT声明:
// 使用整数作为关键字
typedef int Key;
// 记录值
typedef struct value{
int tag;
char message[128];
} Value;
// 记录结点
typedef struct hnode{
Key key;
Value value;
struct hnode *next;
} HNode;
// HashMap对外接口
typedef struct hashmap{
HNode *array; // 数组
int length; // 数组长度
int size; // 散列表的元素个数
} HashMap;
// HashMap函数声明
extern HashMap *hashmap_init(int length);
extern int hashmap_is_empty(HashMap *hashmap);
extern int hashmap_is_full(HashMap *hashmap);
extern int hashmap_add(HashMap *hashmap, Key key, Value *value);
extern int hashmap_delete(HashMap *hashmap, Key key);
extern HNode *hashmap_get(HashMap *hashmap, Key key);
extern void hashmap_traverse(HashMap *hashmap);
extern int hashmap_clear(HashMap *hashmap);
只要明白分离链接法的具体定义,实际上其实现比较简单,这里的散列函数实现使用了简单的取余散列法,你也可以选择其它的散列函数构造法,其它语言中的HashMap差不多也是使用分离链接法,但是在辅助的数据结构上有差别,这里使用的是链表,链表的查询时间是比较慢的,可以将链表换为树加快查询。
以上HashMap实现的完整源码可以在github上查看,main.c文件是HashMap的调用实例:https://github.com/onnple/hashmap,若有任何问题或意见欢迎指出。
2、开放寻址法(Open Addressing)
开放寻址法又叫开放定址法,也是一个常用的解决散列冲突的方法,和分离链接法最大的不同是,开放寻址法不需要辅助的数据结构,仅仅在散列表上进行操作,因为散列冲突的存在,开放寻址法一般比分离链接的散列表大。
开放寻址法使用一个特别的散列方式逐个检查冲突位置的下一个位置,这个函数的一般形式为hi(x)=(hash(x) + f(i))%m,该函数计算第i个散列地址,m是表长,f(i)是i的函数,用于解决冲突,第0个散列值为hash(x),这里提一个平方解决函数:f(i)=f(i – 1) + 2i – 1。下面讨论的线性探测法、平方探测法和双散列法都是函数f(i)的不同,也就是散列函数的不同,其它的都是类似的,而且是在每个位置上进行检测,有冲突则计算下一个位置。
装填因子a=n/m,m为表长,n为关键字数,在这里开放寻址法的搜索期望时间为O(1+a),搜索、插入、删除的时间复杂度为O(1/(1 – a)),一般来说m的选取会比较大,并且尽量让装填因子a小于0.5,这样会有更好的效率。
对于搜索平均开销小于t次探测,线性探测装填因子小于1-1/(根号t),双重散列装填因子小于1-1/t。
(1)线性探测法(Linear Probing)
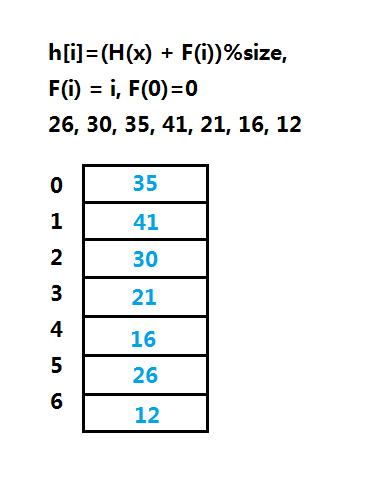
线性探测法的f(i)=i,或关于i的线性函数,线性查找花费的时间较多,占据的单元会形成一个区块,称为一次聚集,装填因子越大,效率越低。
上图线性探测法的一个实例图解,第一次使用的散列函数是hash(x),之后才会使用hi(x)的计算方式,一次计算散列,若发现冲突则计算下一个位置。在实现上m尽量选取素数,对于删除散列表中的元素时不能直接删除,可使用逻辑删除,也就是要用一个成员标记记录的有效性。
(2)平方探测法(Quadratic Probing)
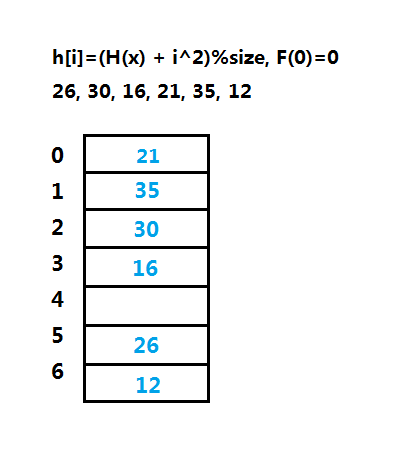
平方探测法可以消除线性探测的一次聚集问题,函数f为f(x)=i^2,只要保证表的一半为空,表长大小为素数,该探测法能保证成功插入一个新的元素,但是仍然有可能插入失败,如果表不够大,实际上开放寻址法都不能保证插入绝对成功。
平方探测法在实现删除操作时可使用逻辑标记删除,一般有三种值:是否已删除、是否已空和是否可用,在三种探测法中,平方探测法更简单速度更快,但是仍然有二次聚集的问题,也就是说映射到同一位置的元素要探测相同的单元。
(3)双散列(Double Hashing)
双散列则是解决平方探测的二次聚集的问题,双散列在三种探测法中效率较为好,函数为f(i)=i * hash2(x),i可取恒值1,双散列是使用第二个散列函数来解决散列冲突。
关于如何构造第二个散列函数hash2(x),有以下几个建议:
- hash2(x)=R – (x % R),R为小于表长m的素数;
- hash2(x)=((x % 97) +1);
- hash2(x)也可以使用取余法,使用不同的质数进行取余。
(4)开放寻址法的代码实现
这里使用开放寻址法实现散列表,同时使用该散列表实现一个HashSet,HashSet的key和value是一样的,这样HashSet的元素是不允许重复的。相应的散列表应用有对单词的拼写检查,但其实和使用HashSet是一样的,将正确的单词加到散列表中,然后根据待检查的单词从表中查找,找不到则表明单词拼写错误。
下面是开放寻址法散列表的ADT声明代码:
#ifndef DATALGORITHM_HASHSET_H
#define DATALGORITHM_HASHSET_H
// 开放寻址法
// 数据实体,同时是关键字和值
typedef struct element{
char name[128]; // 使用name作为关键字
int price;
} Element;
// 数据记录的标记类型
typedef enum kind{
Available, Empty, Deleted
} Kind;
// 数据记录
typedef struct inode{
Element element;
Kind kind;
} INode;
// HashSet对外ADT接口
typedef struct hashset{
INode *array;
int length; // 表长
int size; // 有效的元素个数
} HashSet;
// HashSet函数声明
extern HashSet *hashset_init(int length);
extern int hashset_is_empty(HashSet *hashset);
extern int hashset_is_full(HashSet *hashset);
extern int hashset_add(HashSet *hashset, Element *element);
extern int hashset_delete(HashSet *hashset, Element *element);
extern INode *hashset_get(HashSet *hashset, Element *element);
extern void hashset_traverse(HashSet *hashset);
extern int hashset_clear(HashSet *hashset);
开放地址法实现的散列表并不是很复杂,关键在于散列函数,这里实现的HashSet有提供了上面提到的三种探测法,特别要注意,表长要选择素数,而且开放地址法的填充因子一般是小于0.5,所以存储大量元素是有限的,完整源码可到github查看:https://github.com/onnple/hashset。
3、再散列法(Rehashing)
开放寻址法的一个缺点是,如果数据量较大时会造成插入失败,再散列法就是为了解决问题,实际再散列法比较简单,再散列法就是散列表中的元素数量到一定程度的时候,新申请一个更大的散列表。
那么什么时候重新申请新的散列表呢?这里有以下三个建议:
- 填满一半则进行再散列;
- 插入失败则进行再散列;
- 使用装填因子决定是否进行再散列,这是一个较好的策略,可选0.75、0.6等,但是选择过大可能不会达到预期效果。
既然有再散列,那也要有所收缩,可以在1/8满时,对表进行减半,对表进行再散列时,新的表大小可以查考2k+3,k为素数。
再散列法的总体逻辑为:先用线性探测或其它探测插入数据,若表满到一定程度,至少已存在表的一半次插入,这时新建一个散列表,大小为2k+3素数,重新散列插入数据到新表中,第二次使用的探测方法也可以使用平方探测法或其它方法。
这里使用再散列法实现一个字典Dictionary,和set和map也是一样的,字典Dictionary散列表的说法常见的是Python、C#和Objective-C,实现形式和上面的HashMap是类似的,下面是散列表ADT字典Dictionary的声明代码:
// 散列表使用再散列法实现字典Dictionary
// 关键字
typedef int Keys;
// 数据实体
typedef struct values{
char name[128];
char author[128];
} Values;
typedef enum kinds{
Avail, Emp, Dele
} Kinds;
// 数据记录
typedef struct dnode{
Keys key;
Values value;
Kinds kind;
} DNode;
typedef enum{
Linear, Square
} HashType;
// 字典Dictionary ADT对外接口
typedef struct dictionary{
DNode *array;
int length;
int size;
HashType type;
} Dictionary;
// 字典Dictionary函数声明
extern Dictionary *dict_init(int length);
extern int dict_is_empty(Dictionary *dict);
extern int dict_is_full(Dictionary *dict);
extern int dict_add(Dictionary *dict, Keys key, Values *value);
extern int dict_delete(Dictionary *dict, Keys key);
extern DNode *dict_get(Dictionary *dict, Keys key);
extern void dict_traverse(Dictionary *dict);
extern int dict_clear(Dictionary *dict);
这里实现字典使用了两个探测法:线性探测法和平方探测法,任何再散列都是使用平方探测法,任何收缩散列都是使用线性探测法。再散列会浪费更多空间来换取速度,相对来说,分离链接法会更为灵活一些,但是总的来说,散列表因为使用的是顺序表,普通的实现上需要考虑数据的大小问题,太多的数据无法容纳在内存中。
以上再散列法实现的散列表完整代码,字典Dictionary的完整实现源码可以到github上查看:https://github.com/onnple/dictionary。
4、公共溢出区法
公共溢出区法对于出现冲突的关键字,新建一个溢出表,散列到溢出表,查找时先查找原表,再查找溢出表,该方式并不是很常用,所以这里不侧重讨论该方式,如果你需要实现该方式,实际上也比较简单,当插入失败时就新建一个新的散列表,在设计数据结构时要注意,有必要在总表中保存溢出表的指针。
5、可扩散列(Extendible Hashing)
可扩散列表和B树一样,是一种面向磁盘数据的数据结构,当数据量太大装不进主存时,分离链接法、开放寻址法和再散列法都会造成过多的内存读写。当数据存储在磁盘时,增加速度的关键是减少IO读写次数,在B树中只要在根中保存足够多的关键字,那么可以在几次IO完成读写,B树的时间复杂度为O(Log n)底数为m/2,m为结点的关键字数,当m极大的时候,大到B树只有根和树叶,这时候也就是可扩散列表的模样了。
(1)可扩散列表的定义
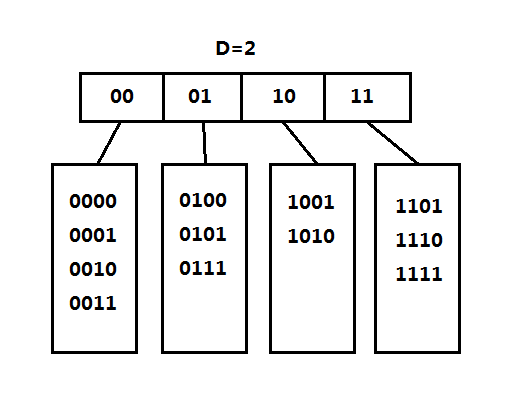
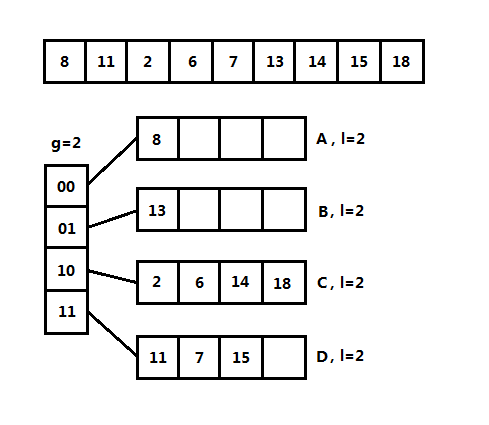
可扩散列表和分离链接法比较相似,首先有一个根表,又称为目录(Directory),目录的每一项保存一个指针指向一个表,也就是树叶。既然是散列表,那么它的关键字和散列函数是怎么样的?可扩散列表将关键字转为二进制的表示形式,将二进制前几位相同的关键字保存在同一个树叶中,例如上图,关键字前两位为00,相同的关键字例如有0000,也就是说目录保存的是相同的几位二进制。
设目录使用的比特数为g位,又称为全局深度(Global Depth),叶子的比特数为l,又称为本地深度(Local Depth),l<=g,目录的项数为2^g,l为叶子中每项最高位相同的位数。这里要注意,究竟是取前g位还是后g位完全可以自定义。
实际上,因为目录的项数为2^g,只要分裂几次,目录就会过大,为了避免目录占据过大的空间,可以让树叶包含记录的指针,而不是实际的数据记录。设n为记录数,树叶的期望个数为(n / g)log e,底数为2,平均树叶满的程度为ln2,约为0.69。
(2)可扩散列表的散列函数
可扩散列表主要是将关键字转为二进制,取关键字的前g位或后g位作为散列地址,下图是一个建议的散列函数处理方式:
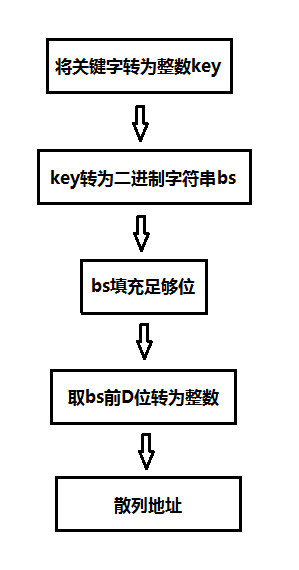
实际上上图还是相对比较复杂,其实还可以直接使用取余散列法,将关键字对目录的项数进行取余,即key%2^g,余数即可作为比特值。
时间关系,这里不对可扩散列表提供代码实现,有兴趣的朋友可以借鉴下面的图解进行实现。
(3)可扩散列表的插入操作
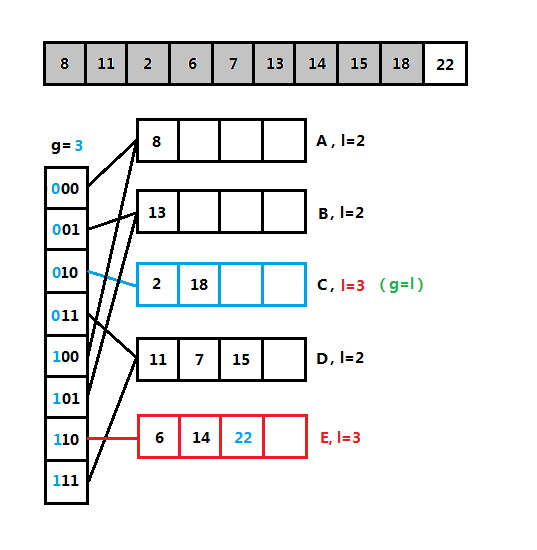
(4)可扩散列表分裂图解
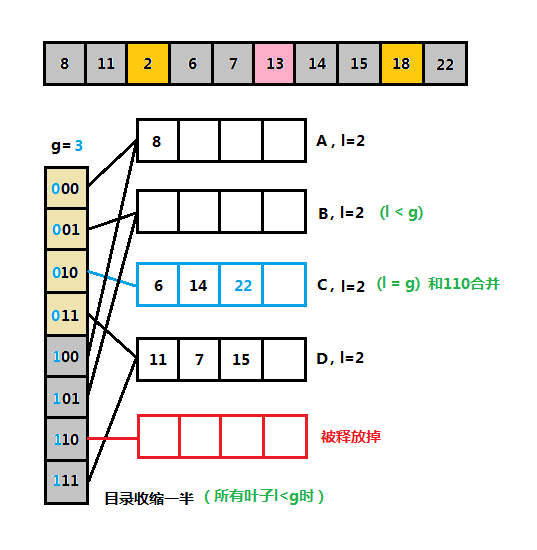
(5)可扩散列表删除和合并图解
四、散列表的应用
1、编程语言数据结构
各种编程语言都有基于散列表的数据结构,基本思想是创建一个键-值key-value对,其中键应该是惟一的值,而不同键的值可以是相同的。这个实现可以在C++中的unordered_set和unordered_map看到,Java中的HashSet和HashMap, python、C#和OC中的dict等。
2、信息摘要和密码验证
这是加密哈希函数的一个应用,密码散列函数是产生输出的函数一般是不可逆性的。常见的散列加密算法有SHA何MD5散列算法,可用于对文件和其它信息的安全校验,包括对密码的加密验证,我们保存用于的密码一般保存的都是密码的散列值,而不是明文,在验证密码的时候将客户端的用户密码计算散列值,发送到服务器和服务器中的散列值进行对比验证。
3、Rabin-Karp算法
Rabin-Karp算法用于匹配字符串,同样也是使用了散列函数,首先给定一个字符串和匹配模式,计算模式字符串的散列值和待匹配的字符串中的进行比较,假设待匹配的字符串长为m,匹配模式长度为n,其匹配次数为O(m – n + 1)。
4、编译器的符号表
编译器中有一个符号表,同样是使用散列表实现,将语言中的关键字保存到散列表中,之后可以用于快速检查关键字。另外将一般的变量和值保存到散列表中,也可以快速追踪源码中声明的变量。
5、图论问题
在图论问题中也用到散列表,关于图数据结构,后面会有讨论。
6、变换表换位表
游戏中基于位置的散列函数,检查对象的位置,通过简单的移动变换避免昂贵的重复计算。
7、单词拼写检查
这个上面有提到,和编译器的符号表是类似的,预先将正确的单词存到散列表中,若使用错误的单词搜索散列表则返回空,这样确定该单词拼写错误。
8、快速查找
这个应用不算很明显的说话,但是任何需要加速访问数据的情形都可以使用散列表,散列表是一个值得常用的数据结构。
9、缓存数据
散列表使用一个散列函数使其执行时间最快可达到常数,在需要数据缓存的情形也大量使用到散列表,在一些数据库如mongodb中也有散列表,另外还有redis和memcached。
 srcmini
srcmini
评论前必须登录!
注册