上一节我们讨论了优先队列和堆的原理和实现,其中堆可用于排序,称为堆排序(heap sort)。本节详细讨论9大经典排序算法,排序算法可以说是我们开发中的一种基本算法,而用到最多的则是快速排序(quick sort),它适用于一般情形,但并不都是最优的,本节还介绍其它算法,某些情况下会比快排好,另外排序算法也是面试中经常遇到的题目(下面介绍的排序算法若无特殊情况一般都是以升序为准)。
一、排序算法的基本概念
排序算法中基本的数据类型是数组,排序的依据可使用简单的数字、字母或字符串。排序的数组大小为n,如果n较小(如小于10^6),则可以在主存中进行排序,又称为内排序,如果n较大,则需要在磁盘上和主存中完成排序,又称为外排序(external sorting)。
整体来说,排序算法又分为两种:基于比较的排序和非比较排序,基于比较的排序使用>大于号、<小于号对两个数进行比较,例如有选择、插入、冒泡排序等,另一种是非比较的排序,如桶排序、基数排序和计数排序,非比较排序一般比较快,使用空间换取时间,下图是完整的排序算法分类(来自网络):
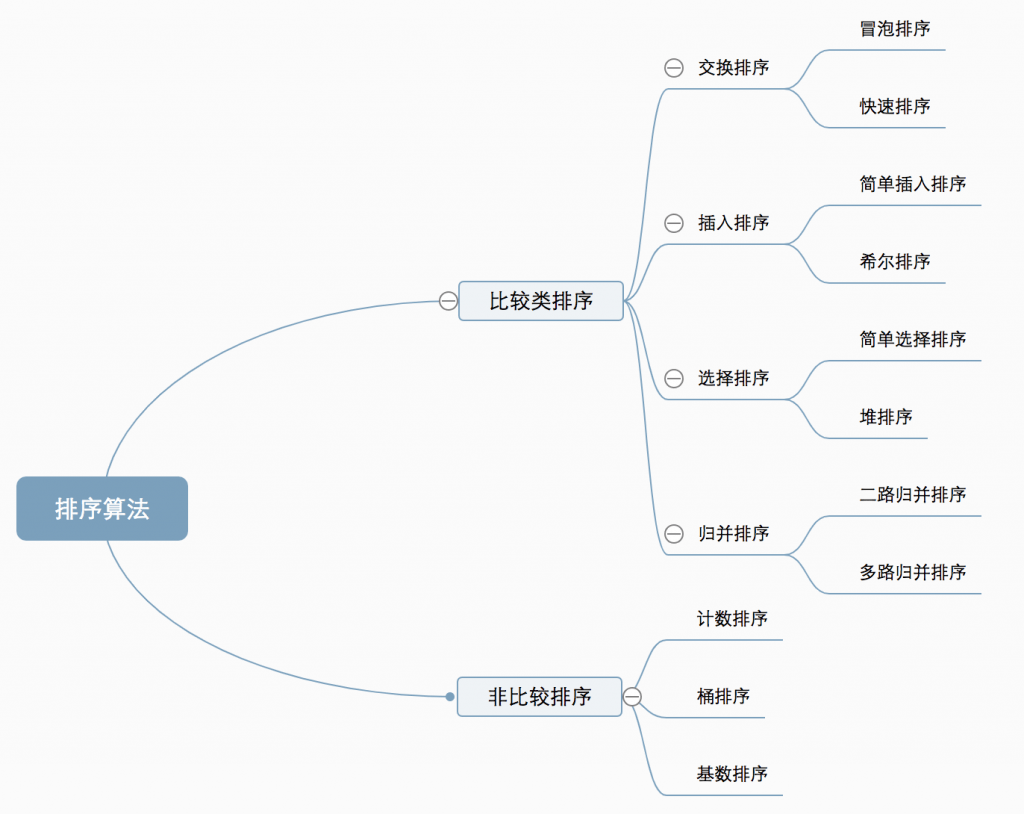
排序算法另一个需要关注的是算法的稳定性,在数组中a在b的前面,并且a=b,若排序后a在b前面,则称该算法稳定,若排序后a在b后面,则称该算法不稳定,至于在实际使用中是否需要考虑排序算法的稳定性,那要看需求(例如预先分析数据是有重复的),像平时我们使用的快速排序则是没有考虑,下图是所有排序算法的复杂度和稳定性的图表(来自网络):
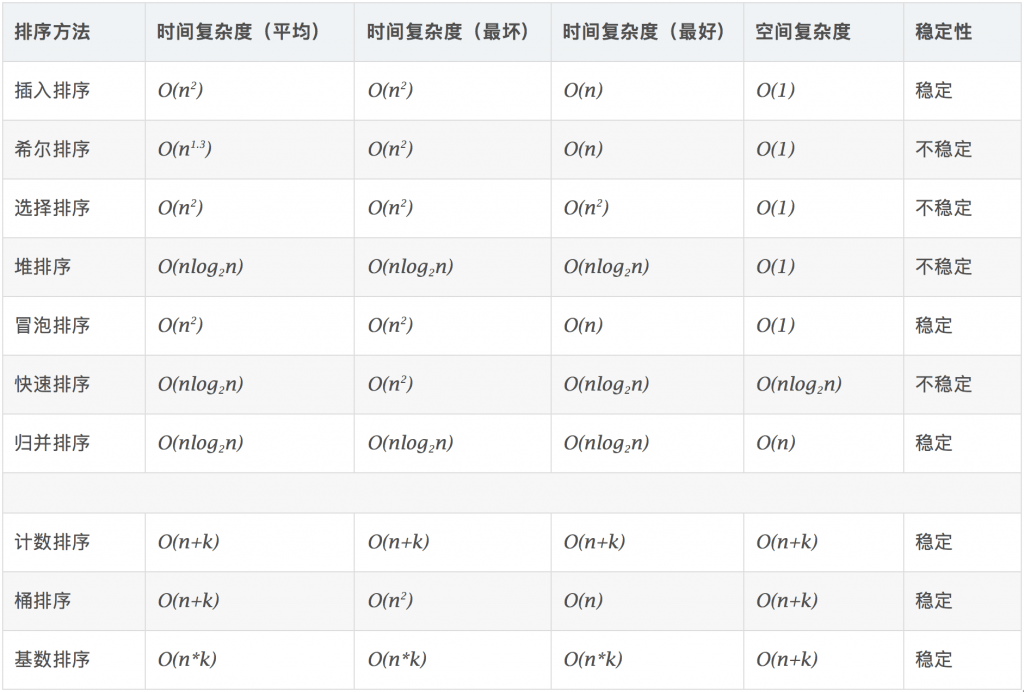
二、选择排序(selection sort)
选择排序是比较简单的排序算法(另外有选择排序的实现原理及其应用详解),其最坏情况为O(n^2),它的算法是:迭代地找出数组右边未排序部分的最小值,将最小值放在左边,动画演示:
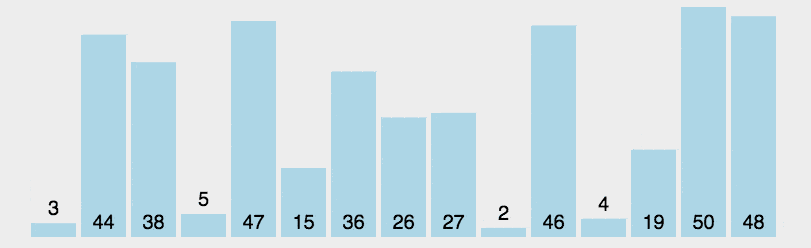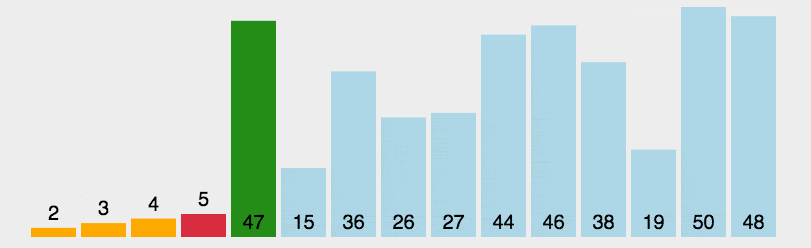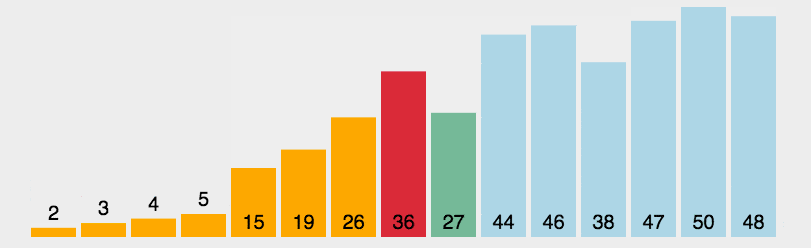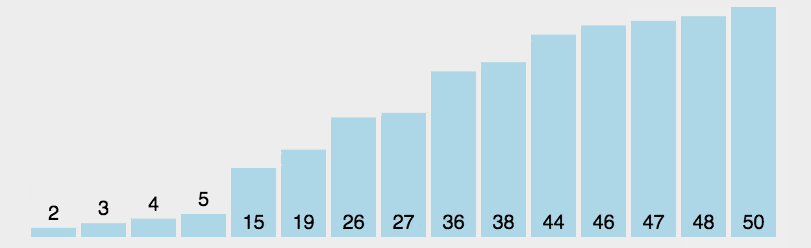
选择排序算法代码实现:
static void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
void selection_sort(int array[], int n){
int i, j, temp;
for (i = 0; i < n; ++i) {
temp = i;
for (j = i + 1; j < n; ++j) {
if(array[j] < array[temp])
temp = j;
}
swap(&array[i], &array[temp]);
}
}
三、冒泡排序(bubble sort)
冒泡排序的时间为O(n^2),也是一个相当简单的基于比较的排序算法,它通过比较相邻的元素,每一轮比较得出一个较大值,将该较大值移到右边,冒泡算法的动画演示如下:
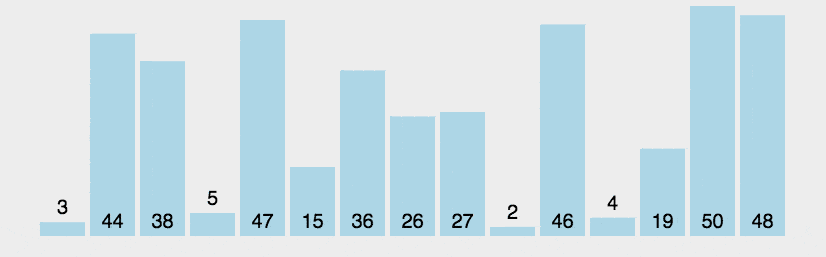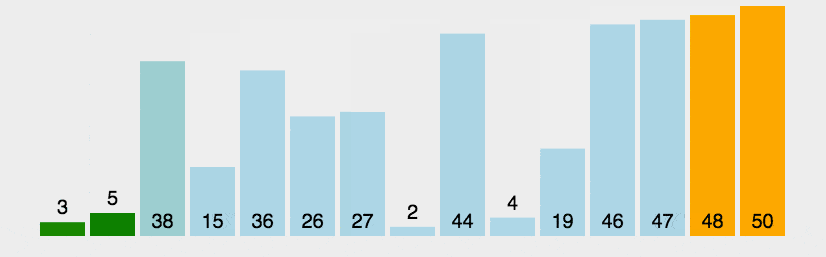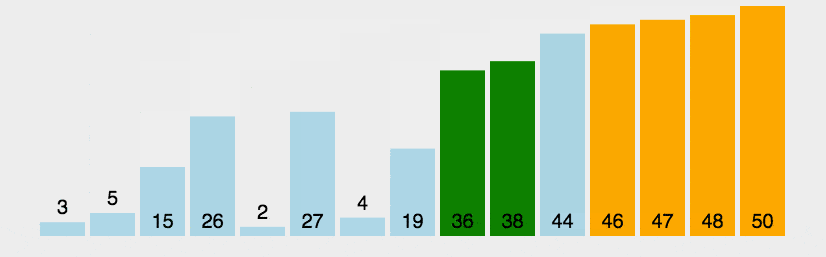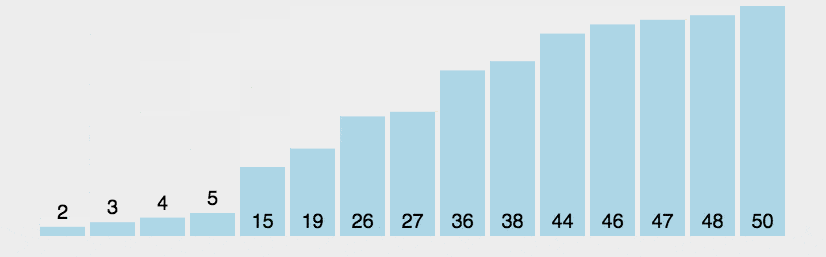
下图是冒泡算法的静态演示例子:
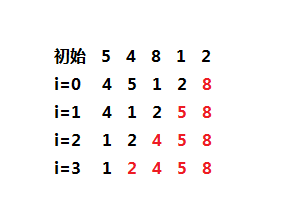
冒泡排序算法实现如下:
void bubble_sort(int array[], int n){
int i, j;
for (i = 0; i < n - 1; ++i) {
for (j = 0; j < n - 1 - i; ++j) {
if(array[j] > array[j + 1])
swap(&array[j], &array[j + 1]);
}
}
}
四、插入排序(insertion sort)
插入排序的最坏时间和平均时间都是O(n^2),插入排序算法从第1个元素开始到第n-1个元素,将当前元素和左边的元素进行比较,持续向左比较相距间隔为1的元素,直到遇到比移动元素小的元素。
在数组A中,满足条件i<j,A[i]>A[j]的两个元素称为逆序对,此时排序算法的运行时间为O(I + n),其中I为数组A的逆序数(逆序对的数量),n个互异数的数组的平均逆序数为n(n-1)/4,因而,通过交换相邻元素进行排序的任何算法平均时间为Ω(n^2)(确定的下界)。
插入排序的算法动画演示如下:
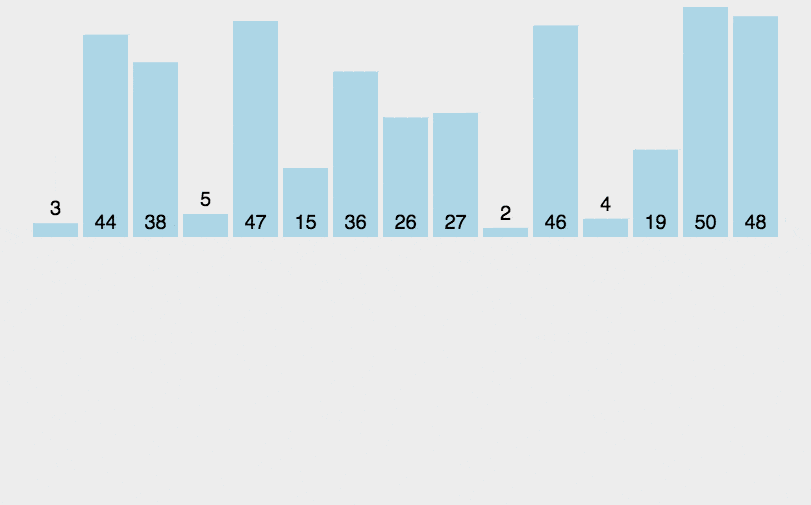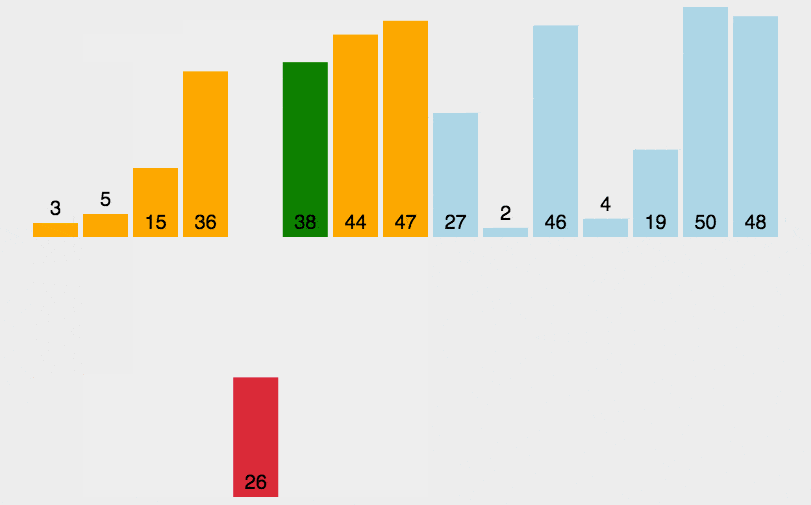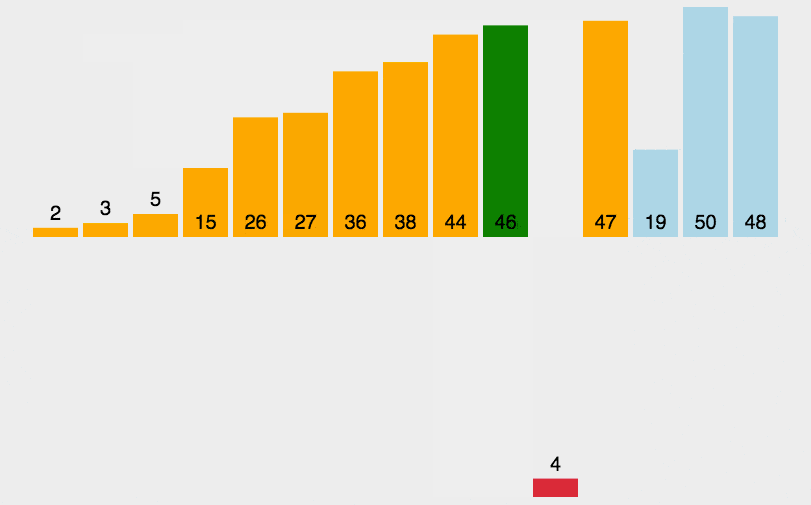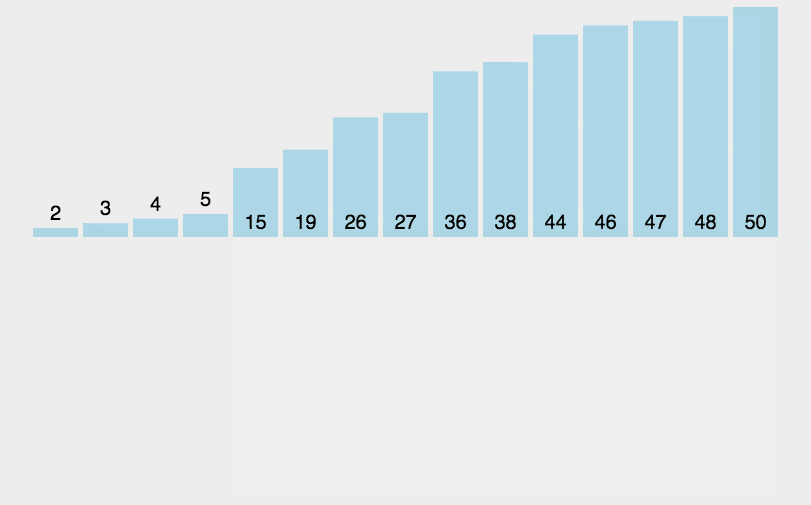
下图是插入排序的静态演示实例:
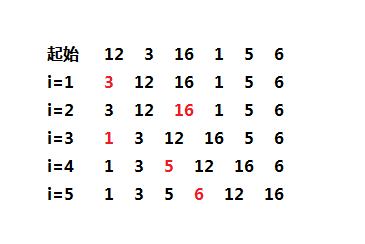
插入排序实现代码如下:
void insertion_sort(int array[], int n){
int i, j, temp;
for (i = 1; i < n; ++i) {
temp = array[i];
for (j = i; j > 0 && array[j - 1] > temp; --j) {
array[j] = array[j - 1];
}
array[j] = temp;
}
}
五、希尔排序(shellsort)
希尔排序的时间为O(n^2),希尔排序是插入排序的一个推广,插入排序是向左边每间隔1个元素比较一次,希尔排序则更灵活,使用一个增量序列h1, h2, …, ht(其中h1=1)对元素进行比较,因而希尔排序又叫做缩小增量排序,对于增量排序,第一步是确定增量函数,例如k(k-1)=hk/2,再确定一个初始化值,如hk=m,使用增量hk的一趟排序后相隔hk的元素都被排序,此时A[i] <= A[i + hk]。常见的增量序列有希尔增量:hk=n/2,Hibbard增量:hk=n/2,hk为奇数,hk为偶数时,hk=hk-1。
其中较好的增量序列为{1, 5, 19, 41, 109, …},通项为9*4^i – 9*2^i + 1或4^i – 3*2^i + 1,希尔排序的关键是在于增量序列,当前也还有其它增量序列。
希尔排序的性质如下:
- hk-排序后序列保留hk-排序性;
- 使用希尔增量时希尔排序的最坏情况为O(n^2);
- 使用Hibbard增量的希尔排序的最坏情况为O(n^(3/2))。
希尔排序的算法如下:
- 确定增量函数(增量序列的选择),例如,初始增量使用ht=n/2,增量递减hk=(k+1)/2,h1=1;
- 每次比较从初始增量ht开始,将A[i]和A[i-ht]的元素进行比较,比较到最后一个增量的位置。
希尔排序的动画演示如下:
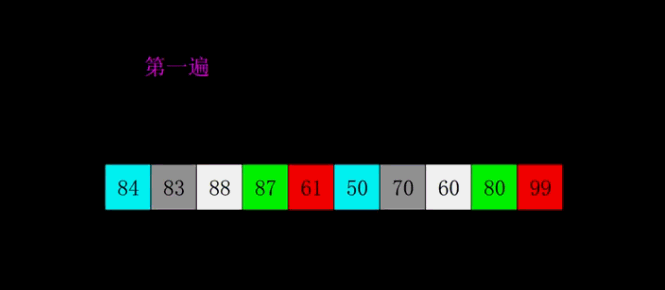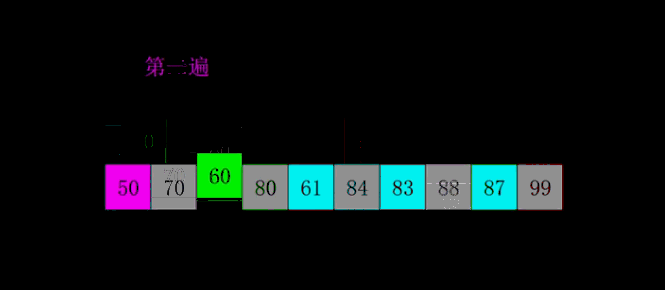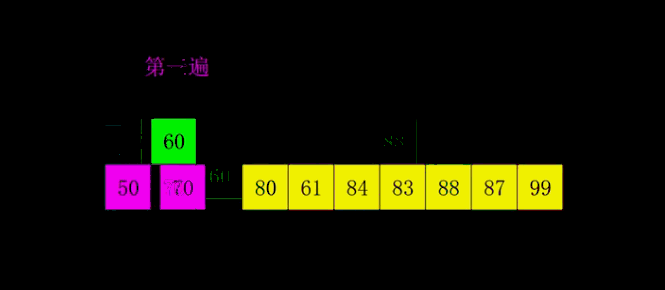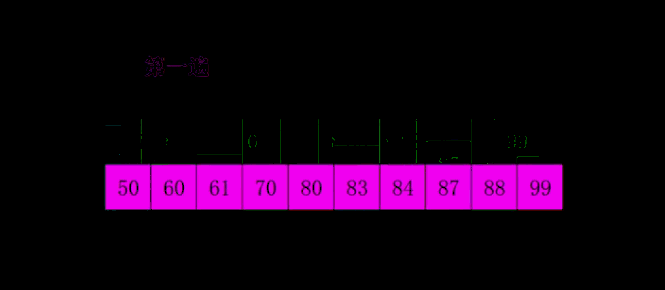
下面是希尔排序的一个实例:
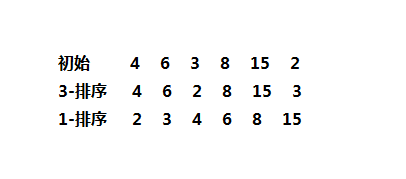
希尔排序算法实现如下:
void shell_sort(int array[], int n){
int i, j, temp, gap;
for (gap = n / 2; gap > 0; gap /= 2) {
for (i = gap; i < n; ++i) {
temp = array[i];
for (j = i; j >= gap && array[j - gap] > temp; j -= gap) {
array[j] = array[j - gap];
}
array[j] = temp;
}
}
}
六、堆排序(heap sort)
上一节我们讨论过优先队列和堆,对于堆排序其最差情况为O(nlog n),但是慢于Sedgewick增量的希尔排序。堆排序使用二叉堆使用,使用数组表示,如果纯属使用二叉堆数据结构,则对数组进行排序需要使用辅助的数组,但是这里堆排序不使用第二个数组,将先出队的元素放到数组末尾,由于放置元素是从结尾到开头,所以,如果是降序则使用最小堆,升序使用最大堆。
对n个互异的随机序列进行堆排序,所用的平均比较次数为2nlog n – O(nlog n)。
堆排序的算法如下:
- 构造最大堆(堆化操作),进行下滤操作;
- 先构建好堆,对前n/2个元素进行下滤操作;
- 进行n-1次出队操作,将出队的元素放到数组结尾。
堆排序的动画演示如下:

下图是另一个堆排序的实例:
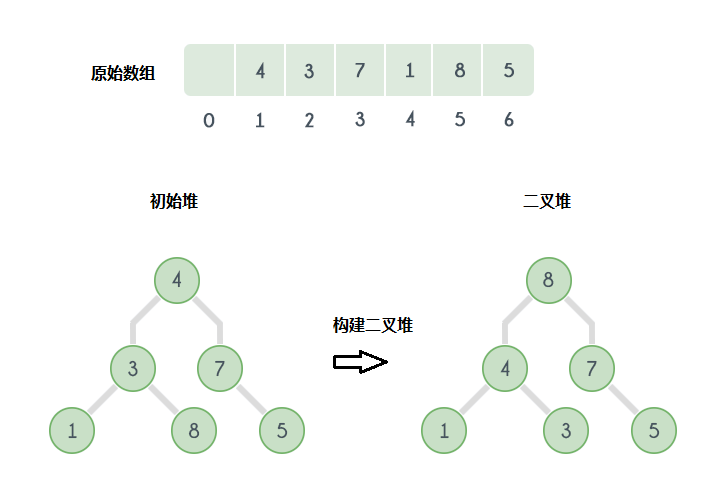
堆排序实现算法如下:
static void heapify(int array[], int i, int n){
int left, child, temp = array[i];
while((left = 2 * i + 1) < n){
child = left;
if(left + 1 < n && array[left + 1] > array[left])
child = left + 1;
if(array[child] > temp)
array[i] = array[child];
else
break;
i = child;
}
array[i] = temp;
}
void heap_sort(int array[], int n){
for (int i = n / 2; i >= 0; --i)
heapify(array, i, n);
for (int j = n - 1; j > 0; --j) {
swap(&array[0], &array[j]);
heapify(array, 0, j);
}
}
七、归并排序(merge sort)
归并排序的最差情况为O(nlog n),归并即是递归和合并的意思,虽然其效果不是很好,但是其排序思想却比较重要,例如下面的快速排序和外部排序都是用到其递归和合并的思想。
归并排序的算法如下:
- 归并排序的主要目的是合并两个已经排好序的数组;
- 首先新建一个和原数组同样大小的辅助数组;
- 对从0到n-1的元素进行分组和合并,分界点为center=(left+right)/2,对左右两部分再次进行分组,最后再合并两部分。
归并排序的缺点是需要附加线性内存,需要将数据拷贝到临时数组再拷贝会原数组,归并排序算法的实例如下:
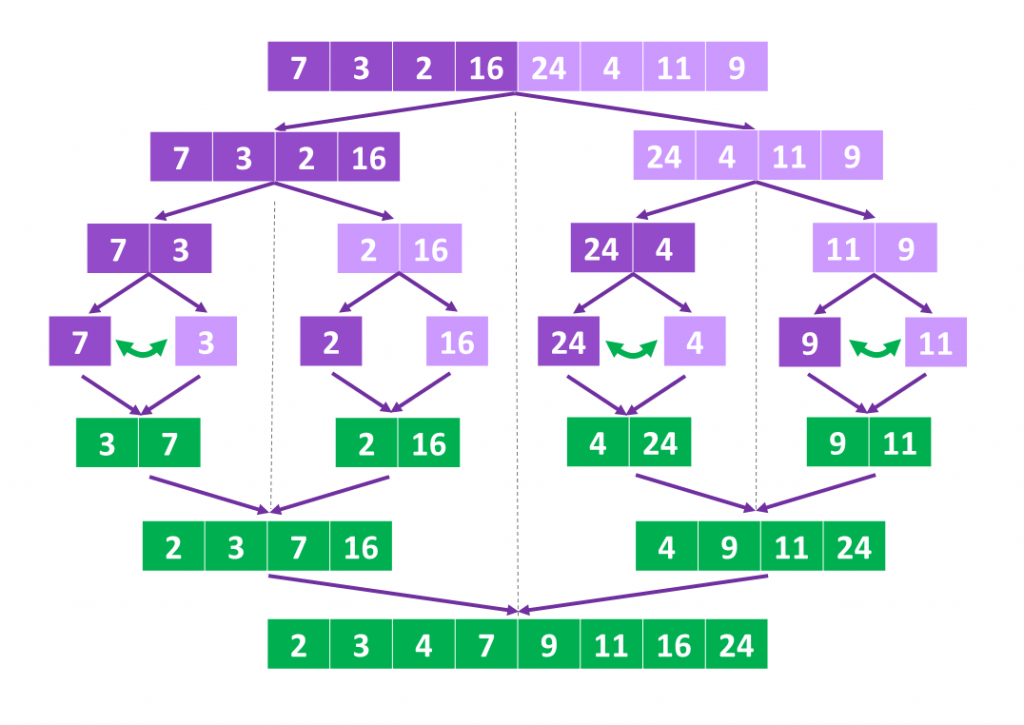
下面是归并排序的算法演示:
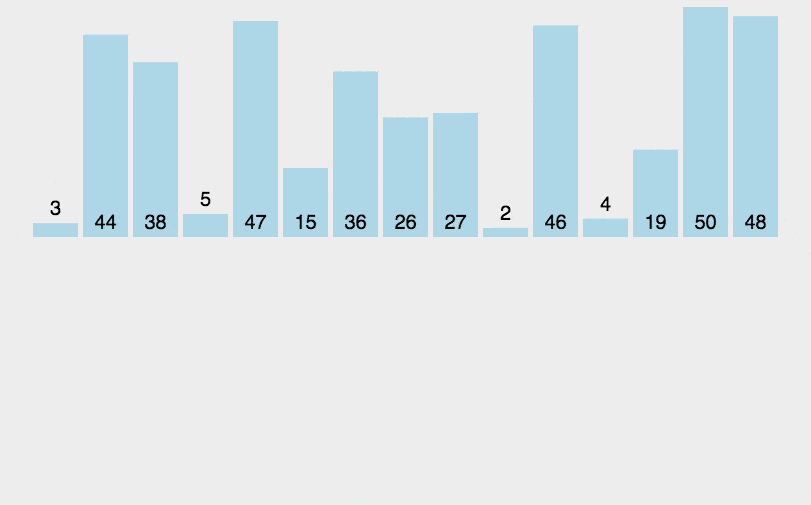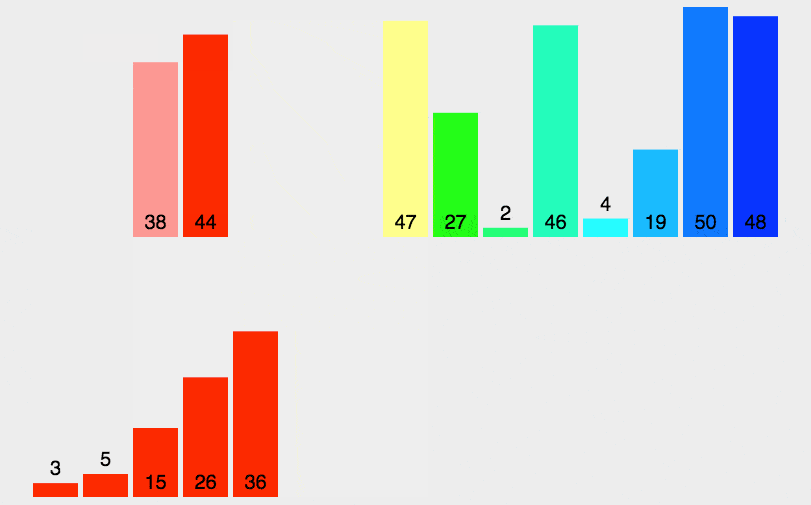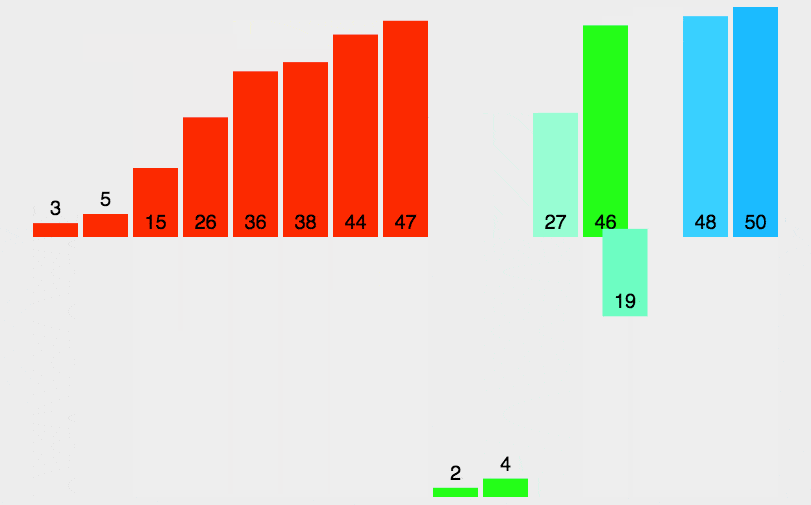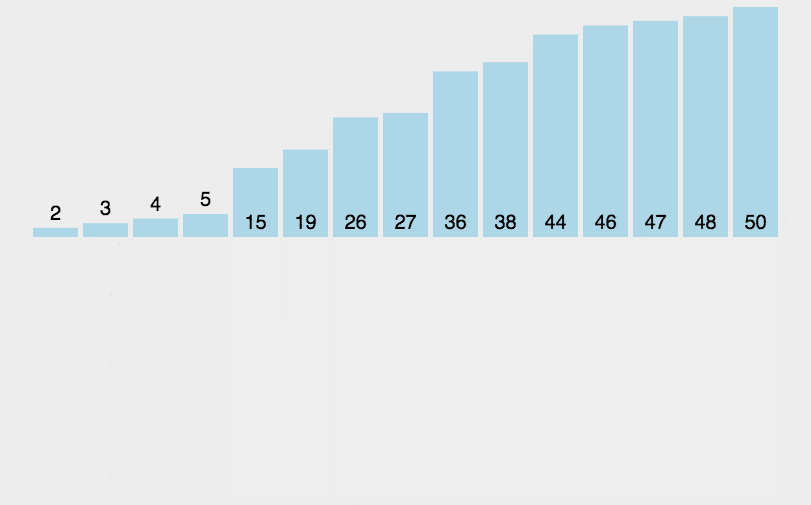
归并排序的算法实现代码如下:
static void merge(int array[], int temp[], int ls, int rs, int re){
int le = rs - 1, t = ls, count = re - ls + 1;
while(ls <= le && rs <= re){
if(array[ls] <= array[rs]){
temp[t] = array[ls];
ls++;
t++;
}
else{
temp[t] = array[rs];
rs++;
t++;
}
}
while(ls <= le){
temp[t] = array[ls];
ls++;
t++;
}
while(rs <= re){
temp[t] = array[rs];
rs++;
t++;
}
for (int i = count; i > 0; --i, re--) {
array[re] = temp[re];
}
}
static void msort(int array[], int temp[], int left, int right){
if(left < right){
int center = (left + right) / 2;
msort(array, temp, left, center);
msort(array, temp, center + 1, right);
merge(array, temp, left, center + 1, right);
}
}
void merge_sort(int array[], int n){
int *temp = (int*)malloc(sizeof(int) * n);
if(temp){
msort(array, temp, 0, n - 1);
free(temp);
}
else{
perror("alloc memory for temp array error");
}
}
八、快速排序(quick sort)
快速排序是目前最快的已知排序算法,但是要注意它的最坏情况为O(n^2),平均运行时间为O(nlog n),快速排序算法的操作方式和上面的归并排序很像,它的算法描述如下:
- 使用递归算法处理数组S,如果S的长度为0或1,返回;
- 在S中任取一个元素pivot,pivot成为枢纽元素,枢纽元素是数组元素数值上的一个值;
- 使用这个枢纽元素将S分割为S1,pivot,S2,按照大于、小于或等于pivot的值,对S进行分割,对于等于pivot的元素,一半放到S1,一半放到S2中;
- 然后对S1、S2分别递归地执行1-3步;
- 执行到最后,S则是已排好序的数组。
下图是快速排序的一个例子:
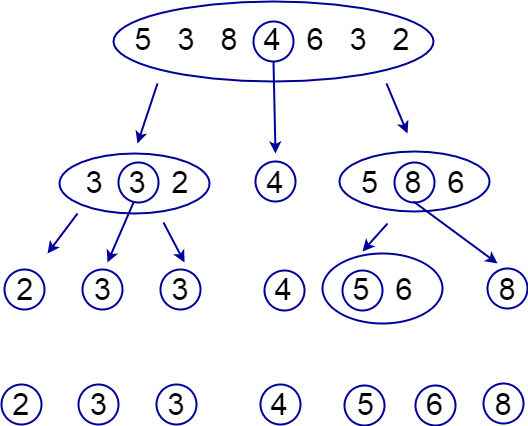
下面向下说一下快速排序算法的细节:
1、选取枢纽元素pivot
(1)不建议使用的方法,使用第一个元素作为枢纽元素,或者使用前两个最大者作为枢纽元素,虽然该方法很快捷,但是有可能造成快排效率较低;
(2)安全的方法,随机选取枢纽元,但是生成随机数昂贵,而且不能保证有更好的算法效率;
(3)三数中值分割法,选取最左最右元素和中间元素:left、right和(left+right)/2,选取中间值的元素作为枢纽元素,推荐使用该方法,下面的实现使用该方法。
2、分割策略
(1)将枢纽元素移到数组的结尾,i从第一个元素开始,j从倒数第二个元素开始;
(2)以枢纽元素为参照,将最小元素移到数组左边,将最大元素移到数组右边;
(3)移动元素和交换元素:
a、i右移动,跳过小于pivot的元素,遇到大于pivot的元素停止,此时位置为k;
b、j左移动,跳过大于pivot的元素,遇到小于pivot的元素停止,此时位置为m,交换位置为k和m的元素;
c、i和j停止时,i指向大元素,j指向小元素,如果i在j的左边,交换这两个元素,否则不用交换;
d、最后将i指向的元素和枢纽元素进行交换。
(4)处理元素等于pivot时的情况:让i和j都停止,进行交换。
在经过以上处理一趟后,此时对于P>i的元素都是大元素,P<i的元素都是小元素。
注意,在这里如果n过小(n<=20),小数组的情况,插入排序的效率会比快排好,可在n<=10时,使用插入排序,下图是快速排序的算法动画演示:
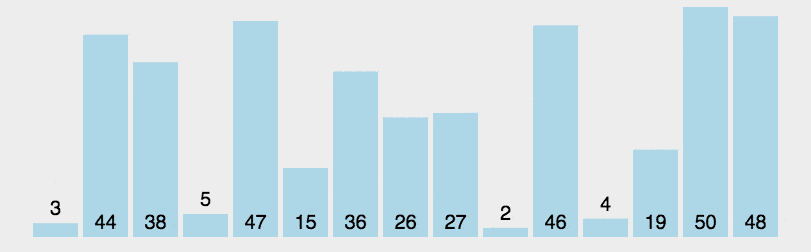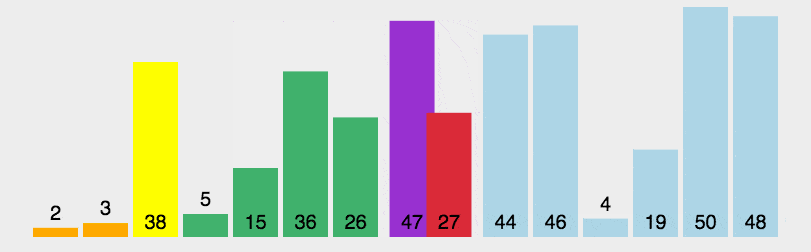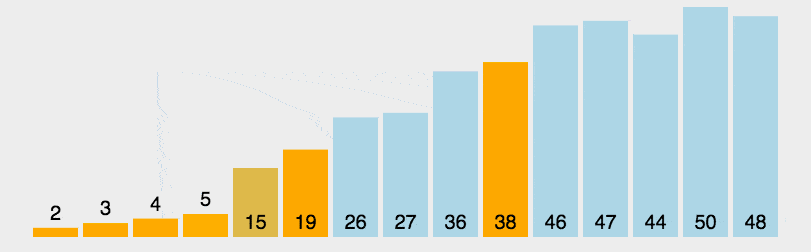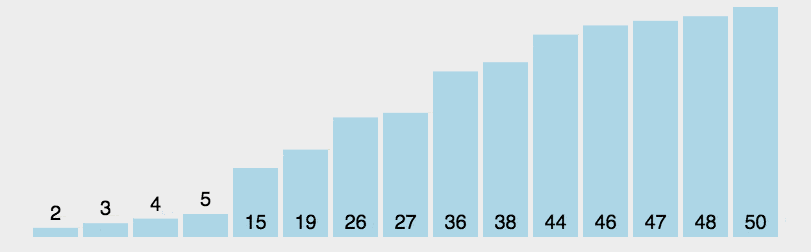
根据以上的描述,排序算法的实现,大概的步骤如下:
- 创建n<=10的条件,该条件下使用插入排序;
- 选取枢纽元素pivot,参考left、right、(left+right)/2,比较这三个位置的元素,以符合A[left] <= A[center] <= A[right],选取A[center]为pivot枢纽元素。将pivot=A[center]放到A[right-1]上(因为pivot = A[center] <= A[right]),分割时j=right-2;
- 分割数组,其实就是递归执行以上步骤;
- 对左右部分递归调用处理。
以上的递归算法也可以解决选择问题,也就是选取第k个最大或最小的元素,算法和快速排序算法是一样的,但是只需要一次递归。
对于排序的一般下界:
- 只使用元素间比较的任何排序算法在最坏情况下至少需要log(n!)次比较;
- 只使用元素间比较的任何排序算法需要进行Ω(nlog n)次比较;
信息理论的下界:存在P种不同的情况需要区分的问题,问题仅仅是YES/NO的形式,那么求解该问题需要logP个问题,这里是对比较排序算法的一些结论。
快速排序的代码实现:
static int get_pivot(int array[], int left, int right){
int center = (left + right) / 2;
if(array[left] > array[center])
swap(&array[left], &array[center]);
if(array[left] > array[right])
swap(&array[left], &array[right]);
if(array[center] > array[right])
swap(&array[center], &array[right]);
swap(&array[right - 1], &array[center]);
return array[right - 1];
}
static void QSort(int array[], int left, int right){
if(left + 3 <= right){
int i, j, pivot;
pivot = get_pivot(array, left, right);
i = left, j = right - 1;
while(1){
while(array[++i] < pivot){}
while(array[--j] > pivot){}
if(i < j)
swap(&array[i], &array[j]);
else
break;
}
swap(&array[i], &array[right - 1]);
QSort(array, left, i - 1);
QSort(array, i + 1, right);
}
else
insertion_sort(array + left, right - left + 1);
}
void quick_sort(int array[], int n){
QSort(array, 0, n - 1);
}
九、桶排序(bucket sort)
桶排序和计算排序、基数排序是类似的,这里介绍具有代表性的桶排序,桶排序的时间为O(m+n),m为数组中的最大元素,桶排序的算法的描述如下:
- 新建一个数组Q,长度为m,其中A[i]<m,也是最大元素加1,将Q初始化为0;
- 扫描A,使得Q[A[i]]=1;
- 扫描数组Q,打印为1的索引即为排序结果。
注意,一般的桶排序算法不能用于小于0的数组,桶排序实现算法如下:
void bucket_sort(int array[], int n){
int max = array[0], i;
for (i = 1; i < n; ++i) {
if(array[i] > max)
max = array[i];
}
max++;
int temp[max];
for (int k = 0; k < max; ++k) {
temp[k] = 0;
}
for (int j = 0; j < n; ++j) {
temp[array[j]]++;
}
int j = 0;
for (int l = 0; l < max; ++l) {
while(temp[l] > 0){
array[j++] = l;
temp[l]--;
}
}
}
十、外部排序(external sorting)
上面介绍都是内部排序,可以直接在主存中执行排序,外排序适合数据量太大而无法装入内存的情况,这时需要将数据装进磁盘或外存,对外存中的数据进行排序。以上的排序算法都是可以直接到内存中寻址,但是直接使用以上的排序算法,对外存数据排序会造成过多IO读取次数,严重损失效率。
外部排序算法整体来说分为两步:构造顺串和合并排序,顺串(run)指定是一个已排好序的序列,构造顺串指的是在初始阶段读取原始数据构造一个个的顺串,合并排序指的是将k个顺序进行合并排序,合并成一个排好序的文件,下面介绍的简单算法、多路合并和多相合并都是合并算法,后面的替换选择是构造顺串的算法。
1、简单算法
执行的IO时间需要log(n/m)趟工作,m为顺串的长度。简单算法是2路合并,2个输入磁带,2个输出磁带,一共4个磁带。设a、b磁带为输入磁带,程序输入已排好序的数据到磁带上,c、d磁带为输出磁带,输出数据到程序进行排序,详细算法如下:
- 每次从a、b磁带读取m个数据,读入到程序并进行排序,排序的算法可使用归并排序的算法,这时排好序的m个数据称为一个顺串;
- 将每个顺串写到c、d磁带上,再分别读取c、d的一组数据进行合并排序,排好序写入a、b;
- 重复以上过程,直到c、d为空,或只剩下一个顺串,则拷贝到适当的顺串上。
下面是使用简单算法的一个例子:

2、多路合并
多路合并也就是上面2路合并的扩展,也是k路合并,这时一共需要2k个磁带,k个输入磁带,k个输出磁带。IO时间,趟树为log(n/m),底数为k,算法过程和以上简单算法类似,可借助优先队列实现。
3、多相合并
多相需要的磁带数为k+1,设有3个磁带,a上有34个顺串:
- 初始化将b写入21个顺串,c为13个;
- b和c合并写入a,a为13个,b为8个,c为0个;
- a和b合并写入c,a为5个,b为0个,c为8个;
- 依此操作,直到一个磁盘上只有一个顺串。
如果顺串的个数是斐波那契数,那么最优的分配为:k+1个磁盘,分为k个斐波那契数。
4、替换选择
替换选择算法是顺串的产生算法,在初始化顺串的时候使用,后面使用归并排序中的合并操作进行合并,详细算法如下:
- 读入m个数据,存到优先队列,优先队列的元素个数为m;
- 执行出队操作,将最小元素写到输出磁带上;
- 继续从输入磁带读入数据,如果比前一个写入的元素大,加入优先队列,执行出队操作,写入输出磁带;
- 如果读入的促进比前一个写入的小,则将新元素存入优先队列的死区(就是优先队列的结尾),用于下一个顺串,同时也进行出队操作,写入输出磁带;
- 依此操作,直到优先队列的元素个数为0,这时使用死区的元素重新构建一个新的优先队列;
下面是构造顺串的一个例子:
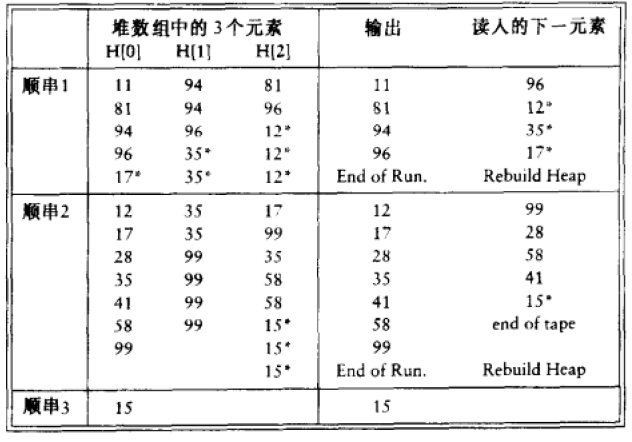
5、外部排序算法实现
外部排序的主要策略是先排序构造顺串,后合并排序,排序构造顺串的步骤是:先读取文件数据进行排序,每次读取一个顺串大小的数据,使用归并排序对每个顺串进行排序,将每个已排序的顺串保存到临时文件,此时一共有k个临时文件或顺串。
后合并排序步骤是:将已排好序的文件合并成一个大文件,也就是k路归并,合并k个已排序的顺串。外部排序的主要算法如下:
- 设输入输出文件名为input和output,output文件合并后的结果文件;
- 确定待排序文件顺串的数量k,顺串的最大长度size(测试方便,可生成一个k*size个数据的文件);
- 创建初始化顺串。创建k个临时文件,创建size大小的数组进行处理数据,每次从文件读取size个数据记录,调用归并排序,将排好序的顺串保存在k个临时文件中;
- 合并文件。也就是k路归并,打开k个临时文件(k个顺串),创建大小为k的最小堆,分别使用k个顺串的第一个元素进行初始化,然后迭代地陆续将最小元素出队,并保存到输出文件中,到此外部排序完成
在以上描述中我们可以看到,外部排序,首先在构造顺串的时候需要使用归并排序,而在合并文件的时候需要使用优先队列,下面是实现外部排序的声明代码:
typedef struct heapnode{
int data;
int i; // 第i个顺串中的数据记录
} HeapNode;
// 二叉堆(最小堆)
typedef struct heap{
HeapNode *array;
int size;
} Heap;
// 优先队列主要使用到的操作
extern Heap *heap_new(HeapNode *datas, int size);
extern HeapNode *heap_min(Heap *heap);
extern void heap_replace_min(Heap *heap);
// 交换数据记录
extern void swap(HeapNode *a, HeapNode *b);
// 归并排序
extern void msort(int array[], int left, int right);
// 外部排序
extern void external_sort(char *input, char *output, int runs, int run_size);
extern FILE* openFile(char* fileName, char* mode);
其完整代码可以在github上查看,其中sorting.h是所有的内部排序算法,esorting.h是外部排序算法:https://github.com/onnple/sortingalgorithms,main.c提供使用实例。
 srcmini
srcmini
评论前必须登录!
注册