JavaScript使用回溯法解决整数分解问题

整数分解问题是这样的：给定一个整数n，假设n可以分解为k个数相加，即x1+x2+x3+…+xk=n，问这样的组合有多少种？也就是说有多少种整数相加为n的组合。

如何使用回溯法解决这个问题呢？首先回溯法的本质在于构建解的状态空间树，然后使用深度优先搜索DFS寻求解，那么如何构建这个空间树呢？

假设n=6，那么在树的根上可以有6个分支（边），也就是从1到6，第6个分支就是一个组合，其它分支需要向下继续扩展分支。例如第1个分支中，使用了1之后只剩下5，将5按照同样的方式进行拆分，这样第5个分支就结束了一组解，即系n=6=1+5，其它分支都是按照类似的方式进行拆分。

在搜索空间树的时候需要进行适当的剪枝，也就是当某一层n<分支上的数时则直接跳过，这么说还是比较抽象，画个图帮助理解吧，如下图：

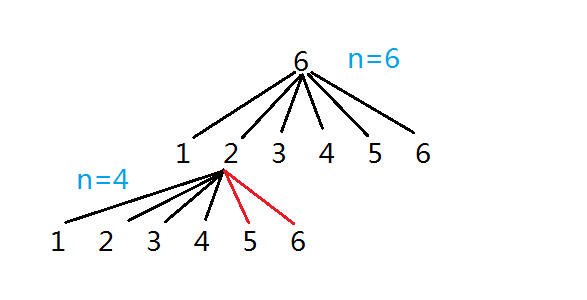
假设在第一个选择2的时候，那么n=6-2=4，也就是下一层只有4可用了，这时就只能选择小于或等于4的数了，所以遇到5和6的时候就要进行剪枝操作。

另外注意，还有一个剪枝操作，那就是那些小于n的数，例如，小于2的数是1，因为这样的组合在第一次选择1的时候已经用过了，所以就不要再用了。

这里使用JavaScript编写整数分解的程序，这里求解的是每种可能的组合，当然你也可以求可能组合的数量，这里求组合使用一个数组储存，当到达树叶（往下不再有解的时候）的时候就输出一个解，到树叶也就是n=0的时候，下面是完整的代码：

// 输出一组解
function prints(s){
    var str = "";
    for(var i = 1;i < s.length;i++){
        str += s[i] + " ";
    }
    console.log(str);
}

// 使用回溯法实现整数分解，回溯法主要是使用DFS的形式
function dfs_split(n, s, p, i){
    if(n == 0){
        prints(s);
        return;
    }
    for(var k = 1;k <= n;k++){
        if(k >= p){
            s[i] = k;
            dfs_split(n - k, s, k, i + 1);
            s.pop();
        }
    }
}

// 调用实例
var n = 10;
var s = new Array();
dfs_split(n, s, 1, 1);