本文概述
使用Python进行机器学习
机器学习是计算机科学的一个分支, 致力于研究可以学习的算法的设计。
典型的任务是概念学习, 功能学习或”预测建模”, 聚类和查找预测模式。这些任务是通过例如通过经验或说明观察到的可用数据来学习的。
该学科带来的希望是, 将经验纳入其任务中将最终改善学习。但是, 这种改进必须以使学习本身变得自动的方式发生, 从而使像我们这样的人不再需要干预是最终目标。
今天的scikit-learn教程将向你介绍Python机器学习的基础知识:
- 你将学习如何在matplotlib和主成分分析(PCA)的帮助下使用Python及其库来探索数据,
- 然后, 你将使用规范化对数据进行预处理, 并将数据分为训练集和测试集。
- 接下来, 你将使用著名的KMeans算法构造一个无监督的模型, 将该模型拟合到你的数据中, 预测值, 并验证你构建的模型。
- 另外, 你还将看到如何使用支持向量机(SVM)来构建另一个模型来对数据进行分类。
如果你对R教程更感兴趣, 请阅读我们的R机器学习入门教程。
另外, 也可以在Python课程中查看scikit-learn和无监督学习的srcmini的监督学习!
加载数据集
数据科学领域的第一步是加载数据。这也是本scikit-learn教程的起点。
该学科通常使用观察到的数据。这些数据可能是你自己收集的, 或者你可以浏览其他来源以查找数据集。但是, 如果你不是研究人员或参与实验, 则可能会做后者。
如果你是新手, 并且想自己解决问题, 那么找到这些数据集可能会是一个挑战。但是, 通常你可以在UCI机器学习存储库或Kaggle网站上找到良好的数据集。另外, 请查看此KD掘金列表以及资源。
现在, 你应该热身, 不必担心自己查找任何数据, 而只需加载Python库scikit-learn随附的digits数据集。
有趣的事实:你是否知道这个名称源于该库是围绕SciPy构建的科学工具箱的事实?顺便说一句, 那里不止一个scikit。该scikit包含专门用于机器学习和数据挖掘的模块, 该模块解释了库名称的第二部分。 🙂
要加载数据, 请从sklearn导入模块数据集。然后, 你可以使用数据集中的load_digits()方法加载数据:
请注意, 数据集模块包含其他方法来加载和获取流行的参考数据集, 并且如果需要人工数据生成器, 也可以依靠此模块。另外, 也可以通过上面提到的UCI存储库获得此数据集:你可以在此处找到数据。
如果你决定从后一页提取数据, 则数据导入将如下所示:
请注意, 如果你像这样下载数据, 则数据已经在训练和测试集中进行了拆分, 扩展名为.tra和.tes。你需要同时加载两个文件才能详细说明你的项目。使用上面的命令, 你只需加载训练集中。
提示:如果你想了解更多有关使用Python数据操作库Pandas导入数据的信息, 请考虑参加srcmini的Python导入数据课程。

探索你的数据
刚开始使用数据集时, 最好先浏览一下数据描述并查看你已经可以学到的知识。当涉及到scikit-learn时, 你不会立即获得此信息, 但是在从其他来源导入数据的情况下, 通常存在数据描述, 该数据描述已经足够收集一些信息。深入了解你的数据。
但是, 这些见识不仅对你将要执行的分析足够深入。你确实需要对数据集有很好的使用知识。
对像本教程现在拥有的数据集执行探索性数据分析(EDA)似乎很困难。
你从哪里开始探索这些手写数字?
收集数据的基本信息
假设你尚未检查任何数据描述文件夹(或者你可能想再次检查已提供给你的信息)。
然后, 你应该从收集必要的信息开始。
当在scikit-learn数据集模块的帮助下打印出数字数据后, 你会注意到已经有很多可用的信息。你已经知道诸如目标值和数据描述之类的内容。你可以通过属性数据访问数字数据。同样, 你也可以通过target属性访问目标值或标签, 并通过DESCR属性访问描述。
要查看哪些键已经可以用来了解你的数据, 你只需运行digits.keys()。
在以下srcmini Light块中尝试全部操作:
你可以(仔细检查)的下一件事是数据的类型。
如果使用read_csv()导入数据, 则将有一个仅包含数据的数据框。不会有任何描述组件, 但是你可以使用head()或tail()来检查数据。在这种情况下, 明智的做法是阅读数据描述文件夹!
但是, 本教程假定你利用库的数据, 并且如果你不熟悉库, 那么digits变量的类型并不是那么简单。查看第一个代码块中的打印输出。你会看到数字实际上包含numpy数组!
这已经是非常重要的信息。但是如何访问这些数组?
实际上, 它很简单:你使用属性来访问相关的数组。
请记住, 当你打印digits.keys()时, 你已经看到了哪些属性可用。例如, 你具有data属性以隔离数据, target具有查看目标值和DESCR的描述, …
但是那又怎样呢?
你应该了解的第一件事就是数组的形状。那是数组中包含的维数和项目数。数组的形状是一个整数元组, 用于指定每个维度的大小。换句话说, 如果你有一个3d数组, 例如y = np.zeros((2, 3, 4)), 则数组的形状将为(2, 3, 4)。
现在, 让我们来看一下你所区分的这三个数组(数据, 目标数组和DESCR数组)的形状。
首先使用data属性将numpy数组与digits数据隔离, 然后使用shape属性查找更多信息。你可以对目标和DESCR执行相同的操作。还有images属性, 基本上是图像中的数据。你还将对此进行测试。
使用数组上的shape属性检查以下语句:
回顾一下:通过检查digits.data, 你看到有1797个样本, 并且有64个要素。因为你有1797个样本, 所以你也有1797个目标值。
但是所有这些目标值都包含10个唯一值, 即从0到9。换句话说, 所有1797个目标值都是由介于0到9之间的数字组成。这意味着模型需要识别的数字为从0到9的数字。
最后, 你看到图像数据包含三个维度:有1797个实例, 其尺寸为8 x 8像素。你可以通过将图像数组重塑为二维来直观地检查图像和数据是否相关:digits.images.reshape((1797, 64))。
但是, 如果你要完全确定, 最好与
print(np.all(digits.images.reshape((1797, 64)) == digits.data))使用numpy方法all(), 你可以测试沿给定轴的所有数组元素的求值是否为True。在这种情况下, 你需要评估调整后的图像数组是否等于digits.data。在这种情况下, 你会看到结果为True。
使用matplotlib可视化你的数据图像
然后, 你可以通过可视化将要使用的图像来提高自己的探索水平。为此, 你可以使用Python的数据可视化库之一(例如matplotlib):
# Import matplotlib
import matplotlib.pyplot as plt
# Figure size (width, height) in inches
fig = plt.figure(figsize=(6, 6))
# Adjust the subplots
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
# For each of the 64 images
for i in range(64):
# Initialize the subplots: add a subplot in the grid of 8 by 8, at the i+1-th position
ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
# Display an image at the i-th position
ax.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest')
# label the image with the target value
ax.text(0, 7, str(digits.target[i]))
# Show the plot
plt.show()乍一看, 代码块似乎很冗长, 这可能会让人感到不知所措。但是, 将代码分解成几部分后, 上面的代码块中发生的事情实际上很容易:
- 你导入matplotlib.pyplot。
- 接下来, 设置一个图形, 图形尺寸为6英寸宽和6英寸长。这是你的空白画布, 所有带有图像的子图将出现在其中。
- 然后转到子图的级别以调整一些参数:将图形的辅助线的左侧设置为0, 将图形的辅助线的右侧设置为1, 将底部的设置为0, 将顶部的设置为1。辅助线之间的空白空间的高度设置为0.005, 宽度设置为0.05。这些仅仅是布局调整。
- 之后, 你将在for循环的帮助下开始填写已完成的图形。
- 你可以一对一地初始化支持, 然后在网格中每个位置乘一个八乘八图像。
- 每次在网格中的每个位置显示一张图像。作为颜色图, 你采用二进制颜色, 在这种情况下将产生黑色, 灰色值和白色。你使用的插值方法是”最近”, 这意味着你的数据插值的方式可能会不平滑。你可以在此处查看不同插值方法的效果。
- 派上的樱桃是在子图中添加了文字。目标标签打印在每个子图的坐标(0, 7)上, 这实际上意味着它们将出现在每个子图的左下角。
- 不要忘了用plt.show()显示剧情!
最后, 你将看到以下内容:

在更简单的注释上, 你还可以使用图像形象化目标标签, 如下所示:
# Import matplotlib
import matplotlib.pyplot as plt
# Join the images and target labels in a list
images_and_labels = list(zip(digits.images, digits.target))
# for every element in the list
for index, (image, label) in enumerate(images_and_labels[:8]):
# initialize a subplot of 2X4 at the i+1-th position
plt.subplot(2, 4, index + 1)
# Don't plot any axes
plt.axis('off')
# Display images in all subplots
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
# Add a title to each subplot
plt.title('Training: ' + str(label))
# Show the plot
plt.show()这将呈现以下可视化效果:

请注意, 在这种情况下, 导入matplotlib.pyplot后, 将两个numpy数组压缩在一起, 然后将其保存到名为images_and_labels的变量中。现在, 你将看到该列表每次包含digits.images实例和相应的digits.target值的suples。
然后, 你说, 对于images_and_labels的前八个元素-请注意, 索引从0开始!-, 你在每个位置的2 x 4网格中初始化子图。旋转轴图, 并在所有子图中显示带有颜色图plt.cm.gray_r(返回所有灰色)的图像, 并且所使用的插值方法最近。你给每个子图标题, 然后显示它。
不太辛苦吧?
现在, 你对将要使用的数据有了很好的了解!
可视化数据:主成分分析(PCA)
但是, 没有其他方法可以可视化数据吗?
由于数字数据集包含64个要素, 因此这可能是一项艰巨的任务。你可以想象很难理解结构并保留数字数据的概述。在这种情况下, 据说你正在使用高维数据集。
数据的高维性是试图通过一系列功能来描述对象的直接结果。高维数据的其他示例包括财务数据, 气候数据, 神经影像学, …
但是, 正如你可能已经聚集的那样, 这并不总是那么容易。在某些情况下, 高维可能会带来问题, 因为你的算法将需要考虑太多的功能。在这种情况下, 你说的是维数的诅咒。因为维数很多, 这也意味着你的数据点实际上与其他所有点都相距甚远, 这使得数据点之间的距离变得无意义。
不过请不要担心, 因为维度的诅咒不仅仅是计算要素数量的问题。在某些情况下, 有效尺寸可能比要素的数量小得多, 例如在某些要素不相关的数据集中。
此外, 你还可以理解, 只有二维或三个维度的数据更容易掌握, 也可以轻松查看。
所有这些都解释了为什么要借助降维技术之一即主成分分析(PCA)来可视化数据。 PCA中的想法是找到包含大多数信息的两个变量的线性组合。这个新变量或”主要成分”可以代替两个原始变量。
简而言之, 这是一种线性变换方法, 可以产生使数据差异最大化的方向(主要成分)。请记住, 方差表示一组数据点之间的距离。如果你想了解更多, 请转到此页面。
你可以借助scikit-learn轻松地将PCA应用到你的数据中:
提示:你在此处使用RandomizedPCA()的原因是, 当尺寸较大时, 它的效果会更好。尝试用常规PCA模型替换随机PCA模型或估计器对象, 看看有什么区别。
注意如何显式告知模型仅保留两个组成部分。这是为了确保你要绘制二维数据。另外, 请注意, 不要将带有标签的目标类传递给PCA转换, 因为你想调查PCA是否揭示了不同标签的分布以及是否可以将实例彼此清楚地分开。
现在, 你可以构建散点图以可视化数据:
colors = ['black', 'blue', 'purple', 'yellow', 'white', 'red', 'lime', 'cyan', 'orange', 'gray']
for i in range(len(colors)):
x = reduced_data_rpca[:, 0][digits.target == i]
y = reduced_data_rpca[:, 1][digits.target == i]
plt.scatter(x, y, c=colors[i])
plt.legend(digits.target_names, bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title("PCA Scatter Plot")
plt.show()看起来像这样:
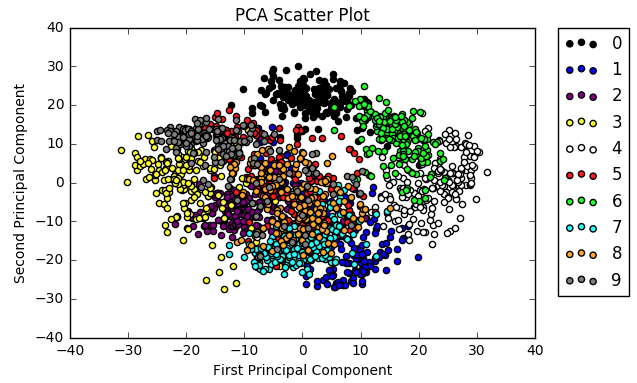
再次使用matplotlib可视化数据。此功能可用于快速可视化你正在使用的内容, 但是如果你正在努力将其纳入数据科学产品组合, 则可能需要考虑一些奇特的事情。
另请注意, 如果你在Jupyter Notebook中工作, 则不需要最后一次调用以显示绘图(plt.show()), 因为你希望将图像插入行内。如有疑问, 你可以随时查阅我们的《 Jupyter Notebook权威指南》。
上面的代码块中发生的事情如下:
- 你将颜色放到一个列表中。请注意, 你列出了十种颜色, 等于你拥有的标签数。这样, 你可以确保可以根据标签对数据点进行着色。然后, 你设置了一个从0到10的范围。请注意, 此范围不包括在内!请记住, 例如, 对于列表的索引, 这是相同的。
- 你设置了x和y坐标。你选取了reduce_data_rpca的第一或第二列, 并且仅选择标签等于你正在考虑的索引的那些数据点。也就是说, 在第一轮中, 你将考虑标签为0的数据点, 然后标签为1…的数据点, 依此类推。
- 你构造散点图。填写x和y坐标, 然后为要处理的批次分配颜色。第一次运行时, 你将为所有数据点赋予黑色, 第二次运行时将其赋予蓝色, 依此类推。
- 你将图例添加到散点图中。使用target_names键为你的数据点获取正确的标签。
- 在你的x和y轴上添加有意义的标签。
- 显示结果图。
现在要去哪里?
现在, 你已经拥有有关数据的更多信息, 并且可以进行可视化处理, 这看上去有点像将数据点归类在一起, 但是你也看到了很多重叠之处。
进一步研究可能会很有趣。
你是否认为, 如果你知道可以为数据点分配10个可能的数字标签, 但是你无法访问这些标签, 则观察结果会按照某种标准以某种方式分组或”聚类”可以推断出标签?
现在, 这是一个研究问题!
通常, 当你对数据有了很好的了解后, 就必须决定与数据集相关的用例。换句话说, 你考虑数据集可能会教给你什么, 或者你认为可以从数据中学到什么。
从那里开始, 你可以考虑可以将哪种算法应用于数据集, 以便获得你认为可以获得的结果。
提示:你对数据越熟悉, 就越容易评估特定数据集的用例。寻找合适的机器算法也是如此。
但是, 当你第一次开始使用scikit-learn时, 你会发现该库中包含的算法数量非常庞大, 并且在评估数据集时可能仍需要其他帮助。这就是为什么此scikit学习机器学习地图会派上用场的原因。
请注意, 此映射确实需要你了解scikit-learn库中包含的算法。顺便说一下, 这对于在项目中进行下一步也具有一些道理:如果你不知道有什么可能, 那么就很难决定数据的用例。
由于你的用例是用于聚类的用例, 因此你可以按照地图上的” KMeans”路径进行操作。你将看到刚才考虑的用例需要拥有50个以上的样本(“检查!”), 具有标记的数据(“检查!”), 以了解要预测的类别数量(“检查!”), 并且样本少于1万(“检查!”)。
但是K-Means算法到底是什么?
它是解决聚类问题的最简单且广泛使用的无监督学习算法之一。该过程遵循一种简单的方法, 通过运行算法之前通过配置的一定数量的群集对给定数据集进行分类。此簇数称为k, 你可以随机选择此数。
然后, k-means算法将为每个数据点找到最近的聚类中心, 并分配最接近该聚类的数据点。
将所有数据点分配给群集后, 将重新计算群集中心。换句话说, 新的群集中心将从群集数据点的平均值中出现。重复此过程, 直到大多数数据点粘贴到同一群集。群集成员身份应稳定。
你已经看到, 由于k-means算法的工作原理相同, 因此你放弃的初始集群中心集可能会对最终找到的集群产生重大影响。当然, 你可以处理这种效果, 你将在后面看到。
但是, 在可以为数据建立模型之前, 你绝对应该考虑为此目的准备数据。

预处理数据
正如你在上一节中所阅读的那样, 在对数据建模之前, 请先做好准备, 以取得良好的效果。该准备步骤称为”预处理”。
数据归一化
我们要做的第一件事是预处理数据。你可以使用例如scale()方法来标准化数字数据:
通过缩放数据, 可以移动每个属性的分布, 使其平均值为零, 标准偏差为1(单位方差)。
将你的数据分为训练和测试集
为了以后评估模型的性能, 你还需要将数据集分为两部分:训练集和测试集。第一个用于训练系统, 而第二个用于评估学习或训练的系统。
实际上, 将数据集分为测试集和训练集是不相交的:最常见的拆分选择是将原始数据集的2/3作为训练集, 而剩下的1/3将构成测试集。
你也可以在这里尝试这样做。你可以在下面的代码块中看到尊重”传统”拆分选择的方式:在train_test_split()方法的参数中, 你清楚地看到test_size设置为0.25。
你还将注意到, 参数random_state分配了值42。使用此参数, 你可以保证拆分将始终相同。如果你想要可重现的结果, 那将特别方便。
将数据集分为训练集和测试集后, 可以在进行数据建模之前快速检查数字:
你会看到训练集X_train现在包含1347个样本(正好是原始数据集包含的样本的2 / 3d)和64个不变的要素。 y_train训练集还包含原始数据集标签的2 / 3d。这意味着测试集X_test和y_test包含450个样本。
聚类数字数据
在完成所有这些准备步骤之后, 请确保已存储所有已知(培训)数据。直到这一刻为止, 还没有进行任何实际的模型或学习。
现在, 终于到了查找训练集中的那些类别的时候了。使用集群模块中的KMeans()来设置模型。你会看到传递给此方法的三个参数:init, n_clusters和random_state。
当你将数据分为训练集和测试集时, 你可能还记得以前的最后一个论点。该论点基本上可以保证你得到可重复的结果。
init指示初始化方法, 即使默认为” k-means ++”, 你也会在代码中看到它的显式出现。这意味着你可以根据需要将其省略。在上面的srcmini Light块中尝试一下!
接下来, 你还将看到n_clusters参数设置为10。该数字不仅指示你希望数据形成的簇或组的数目, 而且还指示要生成的质心的数目。请记住, 簇质心是簇的中间。
你还还记得上一节如何将其描述为K-Means算法的可能缺点之一吗?
那就是你放弃的初始集群中心会对最终找到的集群产生重大影响吗?
通常, 你尝试通过在多个运行中尝试几个初始集合并选择具有最小平方误差总和(SSE)的聚类集来应对这种影响。换句话说, 你要最小化群集中每个点到该群集的均值或质心的距离。
通过将n-init参数添加到KMeans(), 可以确定算法将尝试多少种不同的质心配置。
再次注意, 当你使模型适合数据时, 你不想插入测试标签:这些标签将用于查看模型是否擅长预测实例的实际类!
你还可以按如下所示可视化组成群集中心的图像:
# Import matplotlib
import matplotlib.pyplot as plt
# Figure size in inches
fig = plt.figure(figsize=(8, 3))
# Add title
fig.suptitle('Cluster Center Images', fontsize=14, fontweight='bold')
# For all labels (0-9)
for i in range(10):
# Initialize subplots in a grid of 2X5, at i+1th position
ax = fig.add_subplot(2, 5, 1 + i)
# Display images
ax.imshow(clf.cluster_centers_[i].reshape((8, 8)), cmap=plt.cm.binary)
# Don't show the axes
plt.axis('off')
# Show the plot
plt.show()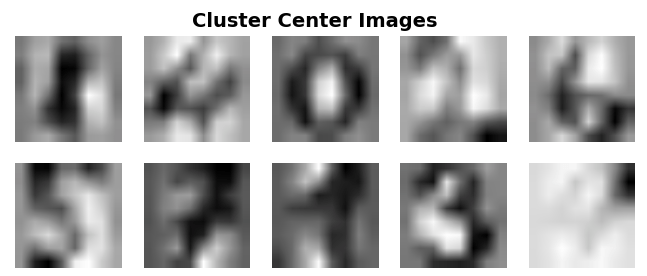
如果要查看另一个可视化数据集群及其中心的示例, 请转到此处。
下一步是预测测试集的标签:
在上面的代码块中, 你将预测包含450个样本的测试集的值。你将结果存储在y_pred中。你还将打印出y_pred和y_test的前100个实例, 然后你会立即看到一些结果。
此外, 你可以研究聚类中心的形状:你立即看到有10个聚类, 每个聚类有64个特征。
但这并不能告诉你太多信息, 因为我们将群集数量设置为10, 并且你已经知道有64个功能。
可视化可能会更有用。
让我们可视化预测的标签:
# Import `Isomap()`
from sklearn.manifold import Isomap
# Create an isomap and fit the `digits` data to it
X_iso = Isomap(n_neighbors=10).fit_transform(X_train)
# Compute cluster centers and predict cluster index for each sample
clusters = clf.fit_predict(X_train)
# Create a plot with subplots in a grid of 1X2
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
# Adjust layout
fig.suptitle('Predicted Versus Training Labels', fontsize=14, fontweight='bold')
fig.subplots_adjust(top=0.85)
# Add scatterplots to the subplots
ax[0].scatter(X_iso[:, 0], X_iso[:, 1], c=clusters)
ax[0].set_title('Predicted Training Labels')
ax[1].scatter(X_iso[:, 0], X_iso[:, 1], c=y_train)
ax[1].set_title('Actual Training Labels')
# Show the plots
plt.show()你可以使用Isomap()来缩小高维数据集数字的尺寸。与PCA方法的区别在于Isomap是一种非线性归约方法。
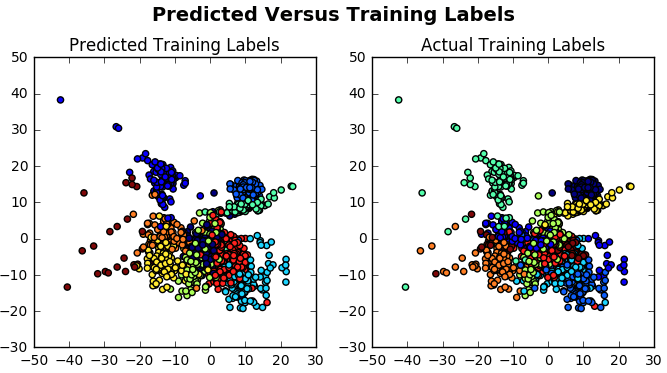
提示:再次从上方运行代码, 但使用PCA缩减方法代替Isomap自己研究缩减方法的效果。
你将在这里找到解决方案:
# Import `PCA()`
from sklearn.decomposition import PCA
# Model and fit the `digits` data to the PCA model
X_pca = PCA(n_components=2).fit_transform(X_train)
# Compute cluster centers and predict cluster index for each sample
clusters = clf.fit_predict(X_train)
# Create a plot with subplots in a grid of 1X2
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
# Adjust layout
fig.suptitle('Predicted Versus Training Labels', fontsize=14, fontweight='bold')
fig.subplots_adjust(top=0.85)
# Add scatterplots to the subplots
ax[0].scatter(X_pca[:, 0], X_pca[:, 1], c=clusters)
ax[0].set_title('Predicted Training Labels')
ax[1].scatter(X_pca[:, 0], X_pca[:, 1], c=y_train)
ax[1].set_title('Actual Training Labels')
# Show the plots
plt.show()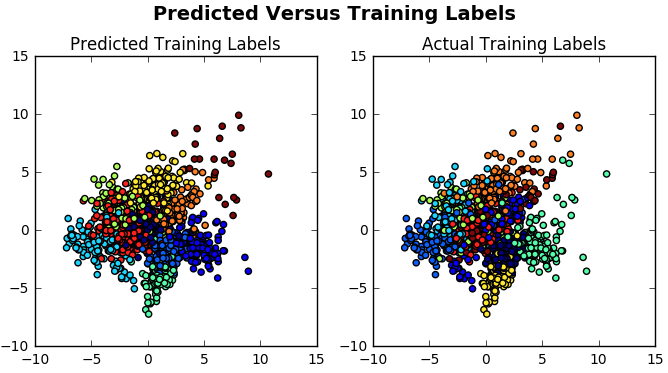
乍看起来, 可视化效果似乎并不表明该模型运行良好。
但这需要进一步调查。
评估集群模型
这种进一步调查的需求将带你进入下一步, 这是对模型性能的评估。换句话说, 你想分析模型预测的正确性。
让我们打印出一个混淆矩阵:
乍看起来, 结果似乎证实了你从可视化中收集到的最初想法。在41个案例中, 只有数字5被正确分类了。另外, 在11个实例中, 数字8被正确分类了。但这并不是真正的成功。
你可能需要了解更多结果, 而不仅仅是混淆矩阵。
让我们尝试通过应用不同的集群质量指标来进一步了解集群质量。这样, 你可以判断聚类标签适合正确标签的好处。
你会发现有很多指标需要考虑:
- 同质性得分告诉你所有聚类在何种程度上仅包含属于单个类的成员的数据点。
- 完整性分数衡量作为给定类的成员的所有数据点也是同一群集的元素的程度。
- V量度得分是均匀性和完整性之间的谐波均值。
- 调整后的兰德评分可衡量两个聚类之间的相似度, 并考虑在预测聚类和真实聚类中分配给相同或不同聚类的所有样本对和计数对。
- 调整后的相互信息(AMI)分数用于比较聚类。它测量聚类中数据点之间的相似性, 并考虑机会分组, 当聚类等效时, 最大值为1。
- 轮廓分数可衡量对象与其自身群集相比其他群集的相似程度。轮廓分数从-1到1, 其中较高的值表示对象与自身的群集更好地匹配, 而与相邻群集的匹配更差。如果许多点具有较高的值, 则集群配置是好的。
你清楚地看到这些分数并不理想:例如, 你看到轮廓分数的值接近0, 这表示样本位于两个相邻聚类之间的决策边界上或非常接近其决策边界。这可能表明样本可能已分配给错误的群集。
另外, ARI指标似乎表明给定群集中的并非所有数据点都是相似的, 而完整性得分则可以告诉你肯定没有正确群集中的数据点。
显然, 你应该考虑使用另一个估计器来预测数字数据的标签。
试用另一种模型:支持向量机
当你回顾了从数据探索中收集到的所有信息时, 你发现可以构建模型来预测数字所属的组而无需知道标签。实际上, 你只是使用训练数据而不是目标值来构建KMeans模型。
假设你不使用数字训练数据和相应的目标值来构建模型的情况。
如果遵循算法图, 你会发现遇到的第一个模型是线性SVC。现在, 将其应用于数字数据:
你将在此处看到使用X_train和y_train将数据拟合到SVC模型中。这显然与集群不同。还要注意, 在此示例中, 你手动设置了gamma值。通过使用诸如网格搜索和交叉验证之类的工具, 可以自动为参数找到合适的值。
即使这不是本教程的重点, 你仍将了解如果使用网格搜索来调整参数, 该怎么做。你将完成以下操作:
接下来, 将分类器与刚刚创建的分类器和参数候选一起使用, 以将其应用于数据集的第二部分。接下来, 你还将使用网格搜索找到的最佳参数训练新的分类器。你可以对结果进行评分, 以查看在网格搜索中找到的最佳参数是否确实有效。
参数确实工作良好!
现在, 这种新知识会告诉你有关在进行网格搜索之前建模的SVC分类器的信息吗?
让我们回到之前制作的模型。
你会看到在SVM分类器中, 错误项的惩罚参数C指定为100。最后, 你看到已将内核明确指定为线性内核。 kernelargument指定你将在算法中使用的内核类型, 默认情况下为rbf。在其他情况下, 你可以指定其他值, 例如线性, 多边形, …
但是什么是内核呢?
核是一个相似度函数, 用于计算训练数据点之间的相似度。当为算法提供内核以及训练数据和标签时, 你将获得分类器, 如此处的情况。你将训练一个将新的看不见的对象分配到特定类别的模型。对于SVM, 通常会尝试线性划分数据点。
但是, 网格搜索告诉你rbf内核会更好。正确指定了惩罚参数和伽玛。
提示:尝试使用rbf内核进行分类。
现在, 假设你继续使用线性核并预测测试集的值:
你还可以可视化图像及其预测的标签:
# Import matplotlib
import matplotlib.pyplot as plt
# Assign the predicted values to `predicted`
predicted = svc_model.predict(X_test)
# Zip together the `images_test` and `predicted` values in `images_and_predictions`
images_and_predictions = list(zip(images_test, predicted))
# For the first 4 elements in `images_and_predictions`
for index, (image, prediction) in enumerate(images_and_predictions[:4]):
# Initialize subplots in a grid of 1 by 4 at positions i+1
plt.subplot(1, 4, index + 1)
# Don't show axes
plt.axis('off')
# Display images in all subplots in the grid
plt.imshow(image, cmap=plt.cm.gray_r, interpolation='nearest')
# Add a title to the plot
plt.title('Predicted: ' + str(prediction))
# Show the plot
plt.show()该图非常类似于你在浏览数据时所做的图:

仅这次, 你将图像和预测值压缩在一起, 并且只采用了image_and_predictions的前四个元素。
但是现在最大的问题是:该模型如何执行?
你清楚地看到, 该模型的性能要比你先前使用的集群模型好得多。
在Isomap()的帮助下可视化预测标签和实际标签时, 你也可以看到它:
# Import `Isomap()`
from sklearn.manifold import Isomap
# Create an isomap and fit the `digits` data to it
X_iso = Isomap(n_neighbors=10).fit_transform(X_train)
# Compute cluster centers and predict cluster index for each sample
predicted = svc_model.predict(X_train)
# Create a plot with subplots in a grid of 1X2
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
# Adjust the layout
fig.subplots_adjust(top=0.85)
# Add scatterplots to the subplots
ax[0].scatter(X_iso[:, 0], X_iso[:, 1], c=predicted)
ax[0].set_title('Predicted labels')
ax[1].scatter(X_iso[:, 0], X_iso[:, 1], c=y_train)
ax[1].set_title('Actual Labels')
# Add title
fig.suptitle('Predicted versus actual labels', fontsize=14, fontweight='bold')
# Show the plot
plt.show()这将为你提供以下散点图:
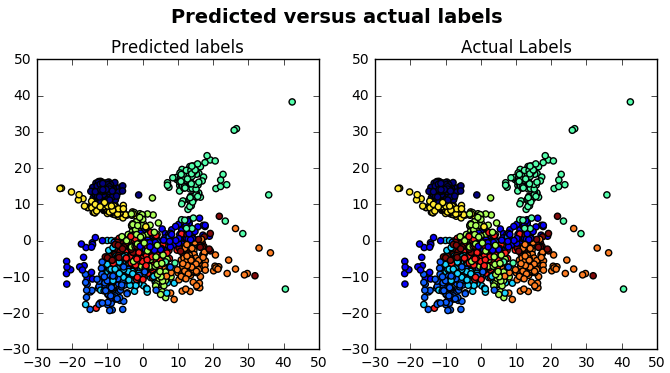
你会看到该可视化确认了你的分类报告, 这是个好消息。 🙂
下一步是什么?
自然图像中的数字识别
恭喜, 你已经完成本scikit-learn教程的结尾, 该教程旨在向你介绍Python机器学习!现在轮到你了。
首先, 请确保你掌握了srcmini的scikit-learn速查表。
接下来, 使用不同的数据启动你自己的数字识别项目。你已经可以使用的一个数据集是MNIST数据, 你可以在此处下载。
你可以采取的步骤与本教程中完成的步骤非常相似, 但是如果你仍然觉得可以使用一些帮助, 则应该查看此页面, 该页面适用于MNIST数据并应用KMeans算法。
使用scikit-learn对字符进行分类的第一步是使用数字数据集。如果你完成了此操作, 则可以考虑尝试一个更具挑战性的问题, 即在自然图像中对字母数字字符进行分类。
可用于此问题的一个著名数据集是Chars74K数据集, 其中包含超过74, 000个数字图像, 从0到9的数字, 以及英文字母的小写和大写字母。你可以在此处下载数据集。
数据可视化和Pandas
无论你是否要从上面提到的项目开始, 这绝对不是使用Python进行数据科学之旅的终点。如果你选择暂时不扩大视图, 请考虑加深你的数据可视化和数据处理知识。
不要错过我们的” Bokeh交互式数据可视化”课程, 以确保你可以用令人惊叹的数据科学作品集或pandas Foundation课程打动你的同行, 以了解有关在Python中使用数据框架的更多信息。
 srcmini
srcmini
评论前必须登录!
注册