本文概述
作为营销经理, 你需要一组最有可能购买你产品的客户。通过这种方式, 可以通过找到受众来节省营销预算。作为贷款经理, 你需要确定有风险的贷款申请, 以降低较低的贷款违约率。将客户分为潜在客户和非潜在客户或安全或有风险的贷款申请的过程称为分类问题。分类是一个分为两个步骤的过程, 即学习步骤和预测步骤。在学习步骤中, 将基于给定的训练数据来开发模型。在预测步骤中, 该模型用于预测给定数据的响应。决策树是最容易理解和理解的分类算法之一。它可以用于分类和回归类问题。
在本教程中, 你将涵盖以下主题:
- 决策树算法
- 决策树算法如何工作?
- 属性选择措施
- 信息增益
- 增益比
- 基尼系数
- 优化决策树性能
- Scikit-learn中的分类器构建
- 利弊
- 总结
决策树算法
决策树是类似于流程图的树结构, 其中内部节点表示要素(或属性), 分支表示决策规则, 每个叶节点表示结果。决策树中最顶层的节点称为根节点。它学习根据属性值进行分区。它以递归方式对树进行分区, 称为递归分区。这种类似于流程图的结构可帮助你进行决策。它的可视化效果像流程图, 可以轻松模仿人类的思维方式。这就是为什么决策树易于理解和解释的原因。
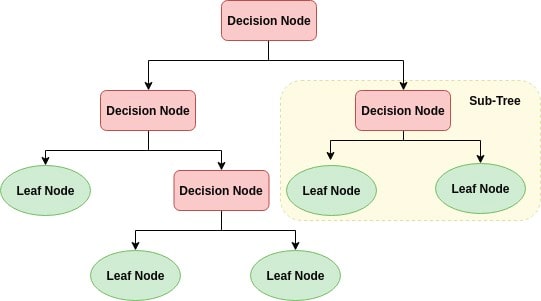
决策树是ML算法的白盒类型。它共享内部决策逻辑, 这在黑盒算法(如神经网络)中不可用。与神经网络算法相比, 它的训练时间更快。决策树的时间复杂度是给定数据中记录数和属性数的函数。决策树是一种无分布或非参数方法, 它不依赖于概率分布假设。决策树可以高精度处理高维数据。
决策树算法如何工作?
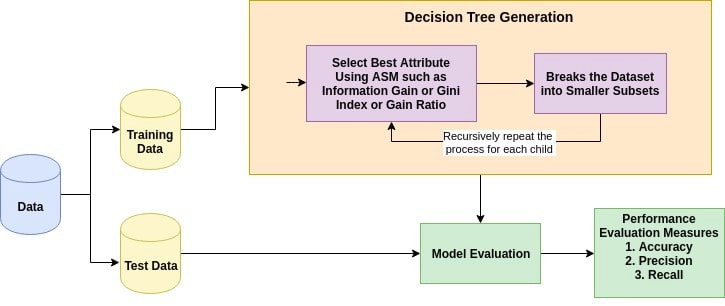
任何决策树算法背后的基本思想如下:
- 使用属性选择度量(ASM)选择最佳属性以拆分记录。
- 使该属性成为决策节点, 然后将数据集分成较小的子集。
- 通过对每个孩子递归地重复此过程来开始树的构建, 直到满足以下条件之一:
- 所有元组都属于相同的属性值。
- 没有更多的剩余属性。
- 没有更多实例了。
属性选择措施
属性选择措施是一种启发式方法, 用于选择将数据划分为最佳可能方式的拆分标准。这也称为拆分规则, 因为它有助于我们确定给定节点上元组的断点。 ASM通过解释给定的数据集为每个功能(或属性)提供等级。最佳分数属性将被选作拆分属性(源)。对于连续值属性, 还需要定义分支的分割点。最受欢迎的选择指标是信息增益, 增益比和基尼系数。
信息增益
香农发明了熵的概念, 它测量输入集的杂质。在物理学和数学中, 熵称为系统中的随机性或杂质。在信息论中, 它是指一组示例中的杂质。信息增益是熵的减少。信息增益基于给定的属性值计算数据集拆分前的熵和拆分后的平均熵之间的差。 ID3(迭代二叉决策器)决策树算法使用信息增益。

其中, Pi是D中任意元组属于类Ci的概率。
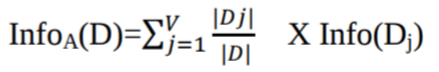
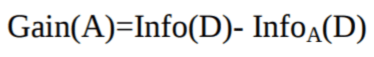
其中,
- Info(D)是识别D中元组的类标签所需的平均信息量。
- | Dj | / | D |充当第j个分区的权重。
- InfoA(D)是基于A的划分从D对元组进行分类所需的预期信息。
选择具有最高信息增益的属性A Gain(A)作为节点N()的拆分属性。
增益比
信息获取因具有许多结果的属性而有偏差。这意味着它更喜欢具有大量不同值的属性。例如, 考虑到具有唯一标识符的属性(例如customer_ID)由于纯分区而具有零info(D)。这样可以最大程度地增加信息增益并创建无用的分区。
C4.5是对ID3的改进, 它使用了信息增益的扩展, 即增益比。增益比率通过使用Split Info标准化信息增益来处理偏差问题。 C4.5算法的Java实现称为J48, 可在WEKA数据挖掘工具中使用。
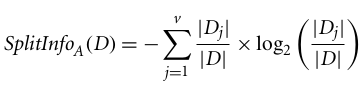
其中,
- | Dj | / | D |充当第j个分区的权重。
- v是属性A中离散值的数量。
增益比可以定义为
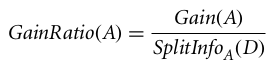
选择具有最高增益比率的属性作为分割属性(源)。
基尼指数
另一种决策树算法CART(分类和回归树)使用Gini方法创建分割点。
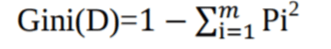
其中, pi是D中的元组属于类Ci的概率。
基尼系数(Gini Index)考虑每个属性的二进制拆分。你可以计算每个分区的杂质的加权和。如果对属性A进行二进制拆分, 则将数据D分为D1和D2, 则D的Gini索引为:
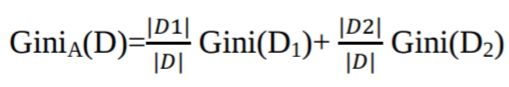
如果是离散值属性, 则将为所选属性提供最小基尼系数的子集选择为拆分属性。对于连续值属性, 策略是选择每对相邻值作为可能的分割点, 并选择基尼系数较小的点作为分割点。
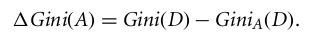
选择基尼系数最小的属性作为拆分属性。
Scikit学习中的决策树分类器构建
导入所需的库
首先加载所需的库。
# Load libraries
import pandas as pd
from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier
from sklearn.model_selection import train_test_split # Import train_test_split function
from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation
加载数据中
首先, 使用熊猫的read CSV函数加载所需的Pima印度糖尿病数据集。你可以在此处下载数据。
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()
| pregnant | glucose | bp | skin | insulin | bmi | pedigree | age | label | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
功能选择
在这里, 你需要将给定的列分为因变量(目标变量)和自变量(或特征变量)两种类型。
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age', 'glucose', 'bp', 'pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable
分割数据
为了了解模型的性能, 将数据集分为训练集和测试集是一个很好的策略。
让我们使用函数train_test_split()拆分数据集。你需要传递3个参数功能, 目标和test_set大小。
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test
建立决策树模型
让我们使用Scikit-learn创建一个决策树模型。
# Create Decision Tree classifer object
clf = DecisionTreeClassifier()
# Train Decision Tree Classifer
clf = clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
评估模型
让我们估计一下分类器或模型预测品种的准确程度。
可以通过比较实际测试设置值和预测值来计算准确性。
# Model Accuracy, how often is the classifier correct?
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.6753246753246753
嗯, 你的分类率为67.53%, 被认为是不错的准确性。你可以通过调整”决策树算法”中的参数来提高此准确性。
可视化决策树
你可以使用Scikit-learn的export_graphviz函数在Jupyter笔记本中显示树。要绘制树, 还需要安装graphviz和pydotplus。
点安装graphviz
点安装pydotplus
export_graphviz函数将决策树分类器转换为点文件, 而pydotplus将此点文件转换为pypy或Jupyter上可显示的形式。
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols, class_names=['0', '1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())

在决策树图中, 每个内部节点都有一个决策规则, 用于拆分数据。基尼系数称为基尼系数, 用于测量节点的杂质。你可以说一个节点的所有记录都属于同一类时就是纯节点, 这种节点称为叶节点。
此处, 未修剪所得树。这棵未经修剪的树无法解释, 也不容易理解。在下一节中, 让我们通过修剪对其进行优化。
优化决策树性能
- 条件:可选(默认=” gini”)或选择属性选择度量:此参数允许我们使用不同的属性选择度量。支持的标准是:基尼系数为”基尼”, 信息增益为”熵”。
- splitter:字符串, 可选(默认=” best”)或Split Strategy:此参数允许我们选择拆分策略。支持的策略是”最佳”选择最佳拆分, “随机”选择最佳随机拆分。
- max_depth:int或无, 可选(默认=无)或树的最大深度:树的最大深度。如果为None(无), 则将节点展开, 直到所有叶子都包含少于min_samples_split个样本。最大深度的较高值导致过度拟合, 而较低的值导致欠拟合(源)。
在Scikit学习中, 决策树分类器的优化仅通过预修剪来执行。树的最大深度可以用作预修剪的控制变量。在以下示例中, 你可以在max_depth = 3的相同数据上绘制决策树。除了预修剪参数外, 你还可以尝试其他属性选择度量, 例如熵。
# Create Decision Tree classifer object
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
# Train Decision Tree Classifer
clf = clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
# Model Accuracy, how often is the classifier correct?
print("Accuracy:", metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.7705627705627706
好了, 分类率提高到了77.05%, 比以前的模型具有更好的准确性。
可视化决策树
from sklearn.externals.six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols, class_names=['0', '1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())

与先前的决策树模型图相比, 此修剪后的模型不那么复杂, 可解释且易于理解。
优点
- 决策树易于解释和可视化。
- 它可以轻松捕获非线性模式。
- 它需要较少的来自用户的数据预处理, 例如, 无需标准化列。
- 它可用于特征工程, 例如预测缺失值, 适用于变量选择。
- 由于算法的非参数性质, 因此决策树没有关于分布的假设。 (资源)
缺点
- 对嘈杂的数据敏感。它可能会过分嘈杂的数据。
- 数据中的小变化(或方差)会导致决策树不同。这可以通过打包和增强算法来减少。
- 决策树因不平衡数据集而有偏差, 因此建议在创建决策树之前平衡数据集。
总结
恭喜, 你已完成本教程的结尾!
在本教程中, 你涵盖了有关决策树的许多详细信息。使用Python Scikit-learn包, 它可以正常工作, 进行诸如信息增益, 增益比和基尼系数之类的属性选择度量, 决策树模型构建, 糖尿病数据集的可视化和评估。此外, 还讨论了其优缺点, 以及使用参数调整来优化决策树性能。
希望你现在可以利用决策树算法来分析自己的数据集。
如果你想了解有关使用Python进行机器学习的更多信息, 请参加srcmini的”使用基于树的模型进行机器学习”课程。
 srcmini
srcmini
评论前必须登录!
注册