适用于MATLAB中基本操作的兼容数组大小

本文概述

• 具有兼容大小的数组输入
• 多维数组输入
• 空数组输入
• 行和列向量兼容性

兼容的数组大小意味着对于每个维度, 输入数组的维度大小都是相同的, 或者其中一个是标量。二进制运算符和函数在具有兼容大小的数组上可以很好地运行。 MATLAB会隐式扩展具有兼容大小的数组, 以使其在执行逐元素操作或函数期间具有相同的大小。

具有兼容大小的数组输入

二维阵列输入

让我们了解具有兼容大小的标量, 向量和矩阵的一些组合：

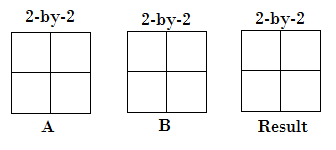
• 两个数组输入的大小完全相同。

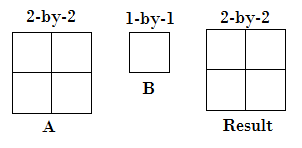
• 一个数组输入是标量。

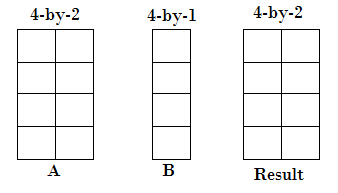
• 一个输入是一个矩阵, 另一个输入是具有相似行数的列向量。

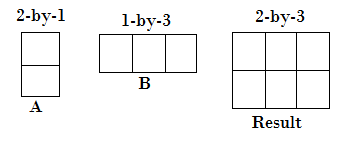
• 一个输入是列向量, 另一个是行向量。

多维数组输入

• 一个输入是矩阵, 另一个输入是具有相同行数和列数的3-D数组。

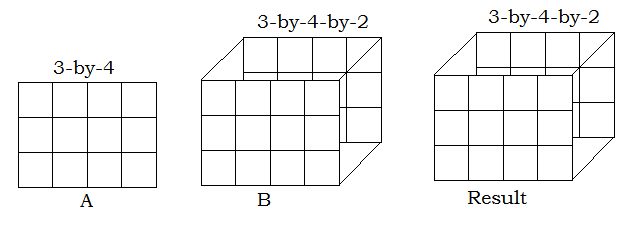
• 一个输入是矩阵, 另一个输入是3D数组。所有输入的尺寸全部相同, 或者输入之一为一维。

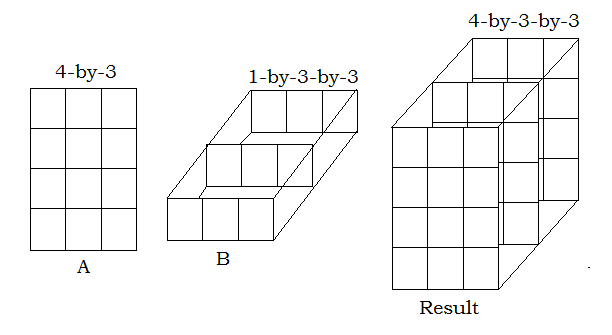
空数组输入

空数组是没有元素且维度大小为零的数组。空数组和非空数组的规则相同, 并且维的大小不等于1决定了输出的大小。

例：

>>% creating empty array
>> a = ones (1, 3, 0)

a =

  1?3?0 empty double array
>> % creating non-empty array
>> b = ones (3, 1);

输出

>> a.*b

ans =

  3x3x0 empty double array

MATLAB会隐式扩展具有兼容大小的数组, 但是无法将不兼容的大小隐式扩展为相同大小。

• 输入尺寸大小之一既不相等也不相等。

例：

>> a = ones(4, 3);
>> b = ones(3, 3);

输出

>> a+b
Matrix dimensions must agree.
>> a-b
Matrix dimensions must agree.
>> a.*b
Matrix dimensions must agree.

• 长度不相等的两个非标量行向量。

例：

>> a =ones(1, 3);
>> b = ones(1, 4);

输出

>> a+b
Matrix dimensions must agree.

>> a-b
Matrix dimensions must agree.

>> a.*b
Matrix dimensions must agree

行和列向量兼容性

行向量和列向量始终具有兼容的大小, 即使大小和长度不同也是如此。然后对这些向量执行算术运算将创建一个矩阵。

例：

>>% creating a row vector
>> a = ones(1, 3)
a =
     1     1     1

>>% creating a column vector
>> b = rand(4, 1)
b =
    0.9058
    0.1270
    0.9134
    0.6324

输出

>>% adding two row and column vectors
>> a + b
ans =
    1.9058    1.9058    1.9058
    1.1270    1.1270    1.1270
    1.9134    1.9134    1.9134
    1.6324    1.6324    1.6324

>>% subtraction of two row and column vectors
>> a - b
ans =
    0.0942    0.0942    0.0942
    0.8730    0.8730    0.8730
    0.0866    0.0866    0.0866
    0.3676    0.3676    0.3676

>>% array multiplication of two row and column vectors
>> a.*b
ans =
    0.9058    0.9058    0.9058
    0.1270    0.1270    0.1270
    0.9134    0.9134    0.9134
    0.6324    0.6324    0.6324