下面列出了最常见的DAA面试问题和答案。
1)什么是算法?
名称”算法”是指必须遵循的说明问题的顺序。
可以执行以执行基本功能的指令的逻辑描述。
算法通常是独立于主要语言而生成的, 即, 可以用一种以上的编程语言来实现一种算法。
阅读更多
2)什么是渐近符号?
一种表示功能在极限或无界的行为的方法。
以域为自然数集合N = {0, 1, 2}的方法描述符号
这样的符号便于定义最坏情况下的运行时间函数T(n)。
它也可以扩展到实数的域。
阅读更多
3)算法的时间复杂度是多少?
算法的时间复杂度表示程序完成运行所需的总时间。通常使用大O表示法表示。
4)解释冒泡排序的算法, 并给出一个合适的例子。
在冒泡排序技术中, 列表分为两个子列表:已排序和未排序。最小的组件从未排序的子列表冒泡。在移动最小的组件后, 假想的墙将向前移动一个元素。最初将冒泡排序写为冒泡列表中的最高项目。但是, 是否冒出最高/最低项目没有区别。此技术易于理解, 但很耗时。在这种类型中, 将比较两个连续的组件, 并完成交换。因此, 在给定” n”个元素列表的情况下, 逐步检查整个数组项, 直到需要n-1次的冒泡排序才能对记录进行排序。
阅读更多
5)解释选择排序的算法并给出一个合适的例子。
在选择排序中, 列表分为两个子列表:已排序和未排序。这两个列表由假想的墙壁分开。我们从未排序的子列表中找到最小的项目, 并将其交换到开头。随着排序文件的增加和未排序文件的减少, 墙将向前移动一项。
假设我们有一个关于n个元素的文件。通过应用选择排序, 将第一项与所有其余(n-1)个元素进行比较。最小的物品放在第一个位置。同样, 将第二项与其余(n-1)个元素进行比较。在比较时, 较小的项目将替换为较大的项目。同样, 检查整个阵列中的最小组件, 然后相应地进行交换。在这里, 我们需要n-1次通过或重复才能完全重新排列数据。
阅读更多
6)解释QUICK排序(分区交换排序)的算法, 并给出一个合适的示例。
Quicksort基于分区。这也称为分区交换排序。快速排序方法的基本概念是从数组中选择一项, 然后围绕它重新排列其余项。该元素将主列表分为两个子列表。所选项目称为枢轴。一旦选择了枢轴, 便会将所有小于枢轴的组件移至值枢轴的左侧, 并将所有高于枢轴的项目移至右侧。递归地测试选择列表的枢轴和划分的过程, 直到子列表仅包含一个元素。
阅读更多
7)什么是NP-Complete?
NP完全问题是NP中的一个问题, 与该类中的任何其他问题一样困难, 因为NP中的任何其他争议都可以在多项式时间内减少。
8)区分时间效率和空间效率?
通过估算基本算法功能执行的次数来衡量时间效率。通过计算算法消耗的额外存储单元的数量来衡量空间效率。
9)算法的顺序是什么?
算法的顺序是算法的标准文档, 已开发该算法来表示任务, 该任务限制了算法的估计时间。算法的顺序是定义其效率的一种方法。它通常称为O标记。
10)什么是蛮力?
蛮力是解决问题的一种直接方法, 通常直接基于问题的陈述和所涉及概念的描述。
11)用来提高算法有效性的各种标准是什么?
输入-外部提供零个或多个数量。
输出-至少构成一个数量
确定性-每条指令简单明了
有限度-如果我们跟踪算法的指令, 那么对于所有步骤, 算法都会在有限数量的步骤后完成
有效性-每条指令必须是基本的。
12)解释用于合并排序的算法, 并给出一个合适的示例。
合并排序的基本概念已将列表分为大小相对相等的两个较小的子列表。递归重复此方法, 直到子列表中只剩下一项。此后, 将各种排序后的子列表合并以形成排序后的父列表。此方法递归进行, 直到原始排序列表到达为止。
阅读更多
13)什么是线性搜索?
线性搜索方法也称为顺序搜索技术。线性搜索是一种在列表中按顺序搜索项目的技术。在这种技术中, 从列表/数组的开始或数组的最后一个组件到数组的第一个组件, 在数组中搜索所需的项, 并继续进行直到找到元素或搜索整个列表/数组为止。
优点
- 这是一种简单而常规的信息搜索技术。线性或顺序名称表示哪些元素是以系统方式存储的。
- 列表中的项目可以按任何顺序排列。即, 可以在排序或未排序的线性数据结构上测试线性搜索。
缺点
- 当列表中存在大量项目时, 此过程不足。
- 它消耗更多时间并降低了系统的检索率。
时间复杂度:O(n)
14)什么是二进制搜索?
二进制搜索高于线性搜索。但是, 无法在未排序的数据结构上对其进行测试。二进制搜索基于分而治之方法。二进制搜索从测试数组中间部分的数据开始。这确定对象是在上半年还是在下半年。如果对象在上半部分, 则无需检查下半部分;如果对象在下半部分, 则无需检查上半部分。同样, 我们重复此过程, 直到在列表中找到对象或从列表中找不到对象为止。在这里, 我们需要三个变量来标识第一个, 最后一个和中间元素。
要实施二进制搜索技术, 该项目必须按排序顺序。
二进制搜索执行如下:
- 将键与数组中间位置的元素进行比较
- 如果键与某个元素匹配, 则将其返回并停止。
- 如果键小于中间位置元素, 则要找到的元素必须在数组的前半部分, 否则必须在数组的后半部分。
- 对数组的下半部分(或上半部分)重复该方法, 直到找到该组件。
阅读更多
15)解释插入排序的算法并给出一个合适的例子。
选择和气泡排序交换项目。但是插入排序不会交换项目。在插入排序中, 将项目插入类似于卡插入的适当位置。在此, 列表分为两个部分:已排序子列表和未排序子列表。在每遍中, 通过将未排序子列表的第一部分插入相关位置, 将其拾取并移入已排序子列表。假设我们有” n”个项目, 我们需要n-1次通过才能对这些项目进行排序。
阅读更多
16)最佳解决方案是什么意思?
给定输入问题, 我们恢复了一个安抚了约束的子集。满足这些约束的任何子集都称为可行解决方案。最大化或最小化给定目的方法的可行解决方案称为最佳解决方案。
17)为什么要散列?
假设我们在数组中存储了大量信息。根据数组是否排序, 在数组中查找项目所需的时间为O(log n)或O(n)。如果对数组进行了排序, 则可以使用诸如二进制搜索之类的过程来搜索数组。否则, 必须线性搜索数组。如果我们需要处理非常高的数据集, 则两种方法都不理想。因此, 我们讨论了一种称为散列的新过程, 该过程使我们能够在恒定时间O(1)中更新和获取任何条目。恒定时间或O(1)性能定义了操作时间量, 而不取决于数据大小n。
阅读更多
18)解释加密算法如何工作?
加密是将纯文本转换为称为” Cliphertext”的密码格式的步骤。为了转换内容, 该算法使用一串称为”密钥”的位进行估计。密钥越大, 用于生成密文的潜在模式的数量越多。大多数加密算法使用固定长度为64到128位的固定输入块代码, 而有些使用流技术。
19)什么是动态编程?
DP是具有最优子结构的另一种解决问题的方法:一个问题的最优解决方案包括子问题的最优解决方案。这并不一定定义每个子问题的最佳解决方案都会对主要解决方案有所帮助。
对于分而治之(自上而下), 子问题是独立的, 因此我们可以按任何顺序解决它们。
对于贪婪的技巧(自下而上), 我们总是可以通过贪婪的选择来选择”正确的”子问题。
在动态编程中, 我们解决了许多子问题并保存了结果:并非所有子问题都将有助于解决更大的问题。由于具有最佳的子结构, 我们可以确定至少有一些子问题将是有用的。
阅读更多
20)什么是背包问题?
给定n个已知权重的元素, wiand值为vi, i = 1, 2? n和容量W的背包, 找出适合背包的元素的最有价值的子集。按值与重量的比率将给定实例的元素按降序排序很方便。然后, 第一个元素给出的最佳重量单位收益, 最后一个给出最差的重量单位收益。
阅读更多
21)什么是Warshall算法?
Warshall的算法是动态编程过程的函数, 用于查找有向图的传递闭包。
22)什么是贪婪算法?
一种针对优化问题的贪婪技术始终会使当前处于最佳状态的选项添加到当前子解决方案中。
阅读更多
23)列出贪婪算法的优势。
- 贪心法产生可行的解决方案
- 贪婪的方法很容易解决问题
- 贪心方法直接实现了最优解
24)什么是最小生成树?
链接图的生成树是一棵树, 其顶点集与给定图的顶点集相同, 并且其边集是给定图的边集的子组。即, 任何链接的图都将具有生成树。
生成树的权重w(T)是T中所有边的权重的总和。最小生成树(MST)是具有最小可行权重的生成树。
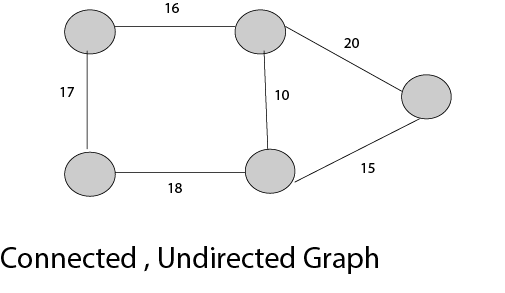
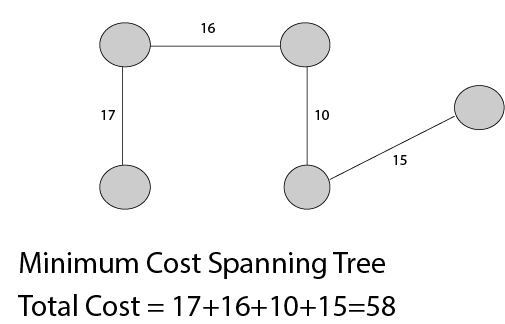
阅读更多
25)什么是Kruskal算法?
这是一种贪婪的方法。贪心方法会选择一些局部最优值(即, 选择MST中权重最小的边)。
Kruskal的算法如下:
制作一个具有’n’个顶点的图形, 继续添加最短(成本最低)的边, 同时避免生成循环, 直到添加(n-1)个边为止。通常, 两个或更多个边缘可能具有相同的速率。在此方法中, 确定边缘的顺序无关紧要。可能会产生不同的”最小生成树”, 但它们的总价格都相同, 这始终是最低成本。
阅读更多
26)什么是分拣网络?
排序网络是用于对一系列数字进行排序的电线和比较器模块网络的数值模型。每个比较器连接两根导线, 并通过将较小的值输出到一根导线, 将较高的值输出到另一根导线来对值进行排序。排序网络与比较排序算法之间的主要区别在于, 对于排序网络, 无论先前的比较结果如何, 都将预先设置一系列比较。比较系列的这种独立性对于并行执行方法很有用。
阅读更多
27)什么是弗洛伊德算法?
弗洛伊德(Floyd)算法是一个函数, 用于查找所有对对的最短路径问题。 Floyd的算法与有向和无向加权图均相关, 但是它们不包括负长度的循环。
28)prim的算法是什么?
Prim的算法是一种贪婪且高效的技术, 用于查找加权链接图的最小生成树。
29)prim算法的效率如何?
prim方法的效率取决于为图形选择的数据结构。
30)什么是Dijkstra的算法?
Dijkstra的算法解决了单源最短路径方法, 该方法可找到从给定顶点(源)到加权图或有向图的另一个顶点的最短路径。 Dijkstra的算法为具有非负权重的图实现了正确的解决方案。
阅读更多
31)霍夫曼树是什么?
霍夫曼树是一种二叉树, 它减少了从根到叶的加权路径长度, 包括一组预定义的权重。霍夫曼树的基本应用是霍夫曼代码。
32)霍夫曼代码是什么意思?
霍夫曼码是一种最佳的前缀树可变长度编码技术, 它根据给定文本中的字符频率将位字符串分配给字符。
阅读更多
33)列出霍夫曼编码的优点?
霍夫曼编码是必不可少的文件压缩技术之一。
- 这很容易
- 灵活
- 它实现了最佳和最小长度的编码
34)什么是动态霍夫曼编码?
在动态霍夫曼编码中, 每次从源文本中读取新字符时, 都会更新编码树。动态霍夫曼n编码用于克服最简单版本的缺点。
35)什么是回溯?
使用边界方法生成深度优先的节点称为回溯。回溯技术的优势在于能够以远远少于m个试验的数量得出解决方案。
阅读更多
36)写下动态编程和贪婪方法之间的区别。
动态编程
- 产生许多决策。
- 始终提供最佳解决方案
贪婪的方法
- 仅生成一个决策序列。
- 不需要总是提供最佳解决方案。
阅读更多
37)Dijkstra算法的用途是什么?
Dijkstra的过程用于求解单源最短路径方法:对于在加权链接图中称为源的给定顶点, 找到到其所有其他顶点的最短路径。单源最短路径过程要求一系列路径, 每个路径都从源通向图中的各个顶点, 尽管某些方向可能具有共同的边。
38)n皇后问题是什么意思?
问题是在n比n的棋盘上放置n个皇后区, 这样就不会有两个皇后通过在同一行或同一列或同一对角线中相互充电。
39)什么是状态空间树?
回溯的处理通过构建一个选择树来解决。这被称为状态空间树。它的根描述了开始搜索解决方案之前的初始状态。树中第一级的节点描述了对解决方案的第一个元素的选择, 第二级的节点描述了对第二个元素的选择, 依此类推。
40)分配问题是什么?
将” n”个人分配给” n”个职位, 以使分配的总价尽可能低。该问题的实例具体化为n-n成本矩阵C, 因此该问题可以描述为在矩阵的每一行中选择一个元素, 这样就不会在同一列中有两个选定的项, 并且总和为最小的。
| 工作/人力资源面试问题 |
| JavaScript面试问题 |
| Java OOP面试问题 |
| JSP面试问题 |
| 休眠面试问题 |
| SQL面试题 |
| Android面试题 |
| MySQL面试问题 |
面试技巧
公司面试问题与程序
Java基础面试问题
Servlet面试问题
春季面试问题
PL / SQL面试问题
Oracle面试问题
jQuery面试问题
 srcmini
srcmini
评论前必须登录!
注册