玻尔兹曼机器是指统一关联的神经元状结构的关联, 该结构做出有关是否开启或关闭的假设决策。 Boltzmann机器由著名科学家Geoffrey Hinton和Terry Sejnowski于1985年发明。Boltzmann机器具有基本的学习算法, 可让他们找到代表训练数据中复杂规律性的令人兴奋的特征。在具有各层特征检测器的网络中, 学习算法通常较慢, 但是在具有单层特征检测器的”受限玻尔兹曼机器”中则较快。通过包括玻尔兹曼机器, 利用其中一个的特征激活作为下一个的训练数据, 可以有效地适应许多隐藏层。
玻尔兹曼机用于解决两个不同的计算问题。首先, 对于搜索问题, 关联的权重是固定的, 并用来表示成本函数。玻尔兹曼机的随机动力学特性使其可以对具有成本函数最小值的二进制状态向量进行采样。其次, 对于一个学习问题, 玻耳兹曼机器已经指出了一组二进制数据向量, 这必须弄清楚如何以高概率生成这些向量。为了解决这个问题, 它必须发现关联的权重, 以便相对于其他可能的二进制向量, 数据向量具有成本函数的最小值。为了解决学习问题, 玻尔兹曼机器对其重量进行了许多小的更新, 每次更新都希望它们能够解决各种各样的搜索问题。
玻尔兹曼机的随机动力学
当第i单元有机会更新其二进制状态时, 它首先计算其绝对输入pi, 它是其自身的偏差qi和来自其他活动单元的关联权重的总和:
Pi = qi +?是的, 我们
其中
wij =它是i和j之间的关联的权重, 并且当j单元打开时mj为1。第i单元以逻辑函数给定的概率开启:
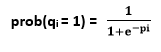
如果单元以不依赖于其总输入的任何顺序连续更新, 则网络最终将达到玻尔兹曼分布(也称为平衡或平稳分布), 其中给定状态向量k的概率完全由与所有可能的二进制状态向量的能量相比, 该状态向量的”能量”:
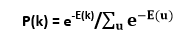
与Hopfield网络一样, 状态向量k的能量定义为
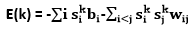
其中, sik是状态向量k指定为单位i的二进制状态。如果选择关联的权重以使状态向量的能量表示这些状态向量的成本, 则可以将玻尔兹曼机的随机动力学视为一种在寻求低成本的同时摆脱不良的局部最优方法的方法。解决方案。单位i的总输入量pi表示取决于单位是关闭还是打开的能量差, 即使pi为负, 单位i有时也会打开的方式意味着在搜索过程中能量有时会增加, 因此允许搜索跳过能量障碍。可以通过使用模拟退火来升级搜索。它按比例缩小所有权重和能量T, 这等于物理网络的温度。通过将T从相当大的初始值减小到较小的最终值, 可以从高温下的快速平衡中受益, 并且仍然具有最终的平衡分布, 这使最小的解决方案比高成本的解决方案更有可能。在零温度下, 更新规则变得确定性, 并且玻尔兹曼机器转换为Hopefield网络。
不同类型的玻尔兹曼机
学习规则可以拥有更复杂的能量函数。例如, 二次能量函数可以由具有公共项si sj sk wijk的能量函数代替。用于更新规则的总输入i必须替换为
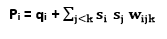
学习规则的重大变化是si sj替换为si sj sk。 Boltzmann机器对数据向量的离散进行建模。但是, 有一个基本扩展, 即”条件玻尔兹曼机”, 用于对条件分布进行建模。可见单位和隐藏单位之间的显着区别是, 在采样(si sj)数据时, 可见单位会被钳位, 而隐藏单位可能不会。如果在采样模型(si sj)时钳制了可见单位的子集, 则该子集充当”输入”单位, 其余的可见单位充当”输出”单位。
学习速度
在具有各种隐藏层的Boltzmann机器中, 学习通常非常缓慢, 因为巨大的网络可能需要很长时间才能达到其平衡分布, 特别是当权重很大且平衡分布是高度多模态时。当可以从平衡分布中获取样本时, 学习信号会非常嘈杂, 因为它是两个样本期望值之间的差异。这些问题可以通过限制网络, 简化学习算法以及一次学习一个隐藏层来解决。
受限玻尔兹曼机:
Smolensky在1986年发明的受限Boltzmann机器。它由一层可见单元和一层隐藏单元组成, 没有可见-可见或隐藏-隐藏的关联。有了这些限制, 隐藏单元在给定可见矢量的情况下将暂时自治, 因此可以在一个并行步骤上获得无偏样本形式(si sj)数据。为了采样形式(si sj), 模型仍然需要进行不同的迭代, 这些迭代在并行还原所有隐藏单元和并行还原所有可见单元之间进行替换。但是, 如果(si sj)model替换为(si sj)reconstruction, 学习仍然可以正常运行, 其结果如下:
从可见单位上的数据向量开始, 并行恢复所有隐藏单位。
并行更新所有可见单元以获得重构。
再次更新所有隐藏的单元。
 srcmini
srcmini
评论前必须登录!
注册