本文概述
作为一名专业的程序员, 你需要在变量, 条件语句, 数据类型, 访问说明符, 函数调用, 作用域等基础知识方面表现出色。无论你正在编写哪种程序, 它都是中间件, 无论是与Web开发还是数据科学相关的程序, 作为程序员, 你都需要在很大程度上了解这些中间件。首先, 你是一名程序员, 然后是数据科学家, Web开发人员或机器学习工程师等。
这样的基本概念就是递归, 在编写特定类型的函数时要知道这一点至关重要。你可能已经知道-“当函数调用自身时, 它称为递归。”但是幕后发生了什么?物理内存如何受递归影响?能否将其他所有函数都转换为递归函数?在本教程中, 你将找到这些基本问题的答案。具体来说, 你将学习:
- 递归函数的基本剖析
- 递归函数的内存表示形式:
- 树
- 堆
- 跟踪递归
- 递归函数的时空分析
- 在Python中实现一个简单的递归函数
递归函数剖析
在你的计算机科学或信息技术本科课程中, 你可能已经遇到过递归一词。在本节中, 你将以有趣的方式重新审视这些概念。让我们开始吧。
让我们再次回到递归的定义:”当函数调用自身时, 它称为递归”。让我们以一个示例来支持此定义:
void A(n){
if(n>=1){
A(n-1);
print(n);
}
}
你可以看到函数A()本身已被调用。这是递归的示例, 而A()是递归函数。
现在让我们研究递归函数的一些基础知识。
递归函数的基础知识:
递归函数必须包含以下两个属性:
- 递归关系
- 终止条件
考虑上面的代码片段以理解这些要点。显然, 该函数具有特定的重复关系:

$ n \ le 1 $是终止条件/锚点条件/基本条件, 如果满足, 递归将停止。必须指定此条件。否则, 函数将陷入无限循环。
(请注意, 以上代码段不遵循任何特定的编程语言。此处的主要目的是显示递归函数的示例。)
你现在必须在思考, 如果有更好的选择, 为什么有人会写一个递归函数?是的, 有时候, 很难跟踪递归, 但是一旦习惯了实践, 就可以在程序的可读性和变量上找到递归。递归不需要额外的变量即可执行, 但需要适当的终止条件才能停止。通常, 很难找到递归的终止条件。再说一次, “实践使你变得完美”。在本教程的后面, 你将看到如果使用递归而不是常规方法来实现程序, 那么该程序可以有多漂亮。现在, 你将继续研究递归函数的内存表示形式。
递归函数的内存表示
在本节中, 你将研究如何通过树和堆栈在内存上基本表示递归函数。让我们考虑以下递归函数A()来理解这一点:
void A(n){
if(n>=1){
A(n-1);
print(n);
}
}
你将首先了解使用树的内存表示形式。听起来可能有点困难, 但确实很简单。如果要以树状方式编写每个函数调用, 它将是什么样?
类似于以下内容?

这里需要注意几点:
- 用A(3)调用该函数, 并在此进行4(3 + 1)个函数调用。如果将其概括化, 则如果调用A(n), 则总共需要(n + 1)个函数调用。
- P()调用是由print(n)产生的打印件。
- 通过A(0)函数调用停止的函数, 因为if语句(在A(0)函数调用之后)将收到n <1, 这将导致函数终止。
你首先看到了这种树状表示, 因为要在堆栈上表示递归函数, 则需要此表示。你现在将看到。
(堆栈是一种数据结构, 其元素的后进快出(LIFO)顺序)
对于堆栈表示, 你将必须以自上而下和左右的顺序遍历树。下图将使这一点变得清楚。

解释这个看起来很奇怪的东西(树)。请记住, 堆栈由两个操作组成-1.按下将元素插入到堆栈中, 然后按下2.弹出, 将元素从堆栈中提取出来。
现在, 你以自上而下和从左到右的顺序开始遍历树:
- 每当你看到函数调用时, 就将其推入堆栈。
- 如果看到print()/ P()调用, 那么你将相应地简单地打印相应的元素。
由于树以自上而下的方式从A(3)遍历到A(0), 因此将成为堆栈的元素:

现在开始树遍历的后半部分, 即左右顺序。每当你第二次看到函数调用时, 你都将弹出它。令人惊讶的是, 要从堆栈中弹出的堆栈的第一个元素(A(0))是进入堆栈的最后一个元素(LIFO, 还记得吗?)。现在, 以你的方式, 你将遇到三个P()调用-P(1), P(2)和P(3)。你将以遍历的方式打印它们。顺序将是:
1 2 3
最后, 当你完成遍历过程时, 堆栈将完全为空。为了更好地理解弹出操作, 这是完全弹出后的堆栈图像。

你已经看到了如何使用树和堆栈将简单的递归函数表示到内存中。现在, 你将看到如何跟踪递归。
跟踪递归
在本节中, 你将学习如何系统地跟踪递归。考虑以下递归函数:
void A(n){
if(n>0){
print(n-1);
A(n-1);
}
}
这里的一个关键点是每当在内存中创建一个称为激活记录的函数时, 该记录包含该函数的局部变量和一个指令指针(表示调用返回该函数时要执行的下一个任务)。将一个称为main()的函数称为上述函数A()作为A(3)。让我们对if语句中的A()行进行编号, 以更好地理解:
void A(n){
1. if(n>0)
2. {
3. print(n-1);
4. A(n-1);
5. }
}
激活记录如下所示:
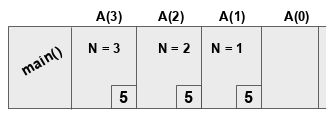
如前所述, 这些函数具有局部变量和指令指针的副本(在本例中为行号)。在A(0)之后, 函数A()将终止弹出操作。请注意, 此处使用的是水平堆栈, 该堆栈与你之前在教程中看到的堆栈完全相同。将记录推入堆栈时, 还将进行打印并打印以下元素:
2 1 0
此处必须注意指令指针, 因为在递归函数中, 控件通常转到相同的函数, 但变量值不同。因此, 保持所有这些同步确实有用。你可以按照此确切过程进行操作, 以便使用树表示形式跟踪递归。
现在, 你将学习如何对递归函数进行时空分析。
递归函数的时空分析
srcmini上有一篇关于Python渐近分析的出色文章, 建议你在阅读本节之前先进行检查。让我们快速回顾一下函数的时空分析(也称为空间复杂度和时间复杂度)的含义:
对于给定的输入, 一个函数应该产生某种输出。为了做到这一点, 该函数需要花费多少时间?时间复杂性测度接近此时间, 也称为函数的运行时。类似地, 空间复杂度度量近似于函数的空间(内存)需求, 即对于给定的输入。但是, 为什么甚至需要这些?
- 你不必在大小可变的输入范围上运行函数, 而是可以轻松估算函数在大小不同的不同输入上的行为方式。
- 如果你有两个函数都实现相同的目标, 那么你将采用哪个函数?你会考虑采取哪些措施来做出决定?是的, 你猜对了。你将通过分析它们的空间和时间复杂性来比较它们, 并查看哪个性能更好。
现在让我们使用一个简单的递归函数, 并分析其空间和时间复杂度。
void A(n){
if(n>1) // Anchor condition
{
return A(n-1);
}
}
首先让我们进行时间复杂度分析。假定上述函数A()花费的总时间为$ T(n)$。现在, $ T(n)$是n大于1进行比较所花费的时间与执行A(n-1)所花费的时间的总和。因此, $ T(n)$可以表示为-
$ T(n)$ = 1 + $ T(n-1)$
1是比较所需的时间(你可以在其中放置任何常量)。现在, 执行A(n-1)的时间是多少(以$ T(n)$表示)?
$ T(n-1)$ = 1 + $ T(n-2)$
同样,
$ T(n-2)$ = 1 + $ T(n-3)$
等等。
如果你密切注意这些方程, 它们都已连接。不是吗如果你一个接一个地替换它们, 则会得到-
$ T(n)$ = 1 +(1 + $ T(n-2)$)= 2 + $ T(n-2)$ = 3 + $ T(n-3)$ = …. = k + $ T(nk)$(在为k个项运行函数之后)
现在, 你需要确定该函数将在什么时候停止。根据给出的锚点条件, 你可以编写-
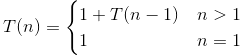
假设在运行了k个条件后, 该函数停止运行。如果是这样, 那么它必须是-
$ n-k = 1 => k = n-1 $
现在将k(= n -1)的值替换为$ T(n)= k + T(n-k)$:
$ T(n)=(n-1)+ T(n-(n-1))$
$ => T(n)=(n-1)+ T(1)$
$ => T(n)= n-1 + 1 = n $ //对于T(1)仅需要比较
根据渐近分析的规则, $ T(n)= n $可以重写为$ T(n)= \ mathcal {O}(n)$。这意味着函数的时间复杂度(最差)为$ \ mathcal {O}(n)$。
你可能希望在这里放慢一点, 并仔细观察此过程的每个步骤。强烈建议你在笔和纸上执行此操作, 以便你可以了解其中的每一点。
该函数的空间复杂度分析很简单。该函数是内存中函数, 不使用任何其他变量。因此, 你可以得出结论, 函数$ \ mathcal {O}(n)$的空间复杂度。
现在, 你将所有这些放在一起, 并在Python中实现一个简单的递归函数。
在Python中实现一个简单的递归函数
你将编写一个递归函数以查找给定数字的阶乘。然后, 你将编写同一函数的迭代版本。让我们开始吧。
# Recursive function factorial_recursion()
def factorial_recursion(n):
if n == 1:
return n
else:
return n*factorial_recursion(n-1)
# Call the function
num = 7
print("The factorial of ", num, " is ", factorial_recursion(num))
The factorial of 7 is 5040
还记得编写递归函数的两个关键要素吗?
- 递归关系
- 终止条件
在这种情况下, 递归关系可以是-
$ f(n)= n!$
$ f(n)= n * f(n-1)$等。
终止条件是当n等于1时。
简单吧?
现在, 你将实现同一函数的迭代版本。
def factorial_iterative(num):
factorial = 1
if num < 0:
print("Sorry, factorial does not exist for negative numbers")
elif num == 0:
print("The factorial of 0 is 1")
else:
for i in range(1, num + 1):
factorial = factorial*i
print("The factorial of", num, "is", factorial)
factorial_iterative(7)
The factorial of 7 is 5040
你可以清楚地发现两个版本之间的差异。递归版本比迭代版本更漂亮。是不是
恭喜!
你已经做到了最后。在本教程中, 你对递归函数进行了广泛的研究。从绝对的基础知识开始, 再到分析递归函数的时空复杂性, 你已涵盖了所有内容。你还看到了递归对于解决具有特定特征的问题有何好处。现在, 你应该可以使用递归来解决问题(具有递归关系和终止条件)。你可能要解决使用递归查找范围内的斐波那契数的问题。
我将坚持要求你使用递归来解决一些常见问题, 例如二进制搜索, 合并排序, 河内塔等, 并执行时空分析。这肯定会使你成为更好的程序员。
从介绍的角度来看, 你所介绍的内容已足够。但是, 如果你想研究有关递归的更多信息, 请确保你访问以下链接:
- 递归和字典, Grimson教授
- 动态编程可优化递归函数的性能
如果你想了解有关Python的更多信息, 请参加srcmini的免费的Python数据科学入门课程。
 srcmini
srcmini
评论前必须登录!
注册