本文概述
在这篇文章中, 你将被介绍到深度学习的神奇世界。本教程将主要涵盖深度学习和神经网络的基础知识。你将学习深度学习中使用的一些基本概念和术语, 并了解为什么深度学习技术在当今如此强大。不仅如此, 你还可以自行构建一个简单的神经网络, 并使用python的numpy库生成预测。
提示:要获得有关人工智能, 机器学习和深度学习的一些背景知识, 请考虑阅读有关机器学习和深度学习之间的差异的文章, 或者对于机器学习的简介, 此简短教程可能会有所帮助。
介绍
假设你在一家贷款公司工作, 并且需要建立一个模型来预测用户(借款人)是否应该获得贷款?你具有每个客户的功能, 例如年龄, 银行存款余额, 年薪(无论是否退休)等等。

考虑如果你想使用线性回归模型来解决此问题, 则线性回归将假设结果(无论是否应批准客户的贷款)将是所有特征的总和。它将考虑年龄, 工资, 银行结余, 退休状态等的影响。因此, 线性回归模型没有考虑这些功能之间的相互作用或它们如何影响整个贷款过程。

上面的左图(A)显示了完全没有相互作用的线性回归模型的预测, 其中简单地将年龄(30>年龄> 30)和银行结余的影响相加, 你可以从图(A)中观察到线性回归模型假定的两条平行线反映了交互作用。
另一方面, 右图(B)显示了来自模型的预测, 该模型允许交互作用, 其中线条不必平行。神经网络是一种非常好的建模方法, 它可以很好地进行如图(B)所示的交互, 并且从这些神经网络中发展出一个称为”深度学习”的术语, 该术语使用了这些强大的神经网络。因为神经网络很好地考虑了这些类型的交互, 所以它可以在你迄今为止已经看到或可能没有听到的许多预测问题上表现良好。
由于神经网络能够处理这种复杂的交互作用, 因此它们具有解决挑战性问题并执行令人惊奇的事情的能力
- 图片
- 文本
- 音讯
- 视频
该列表只是神经网络能够解决的问题的一个子集, 几乎你可以在数据科学领域中想到的任何事物都可以使用神经网络来解决。
深度学习甚至可以学习为你编写代码。好吧, 那不是超级神奇吗?
神经网络中的相互作用

神经网络架构看起来类似于上图。最左边的输入层包含年龄, 年薪, 银行结余等功能, 最右边的输出层输出模型的预测, 在这种情况下, 客户是否应该获得贷款。
除输入和输出层之外的层称为隐藏层。
现在的问题是为什么它们被称为隐藏层?
好吧, 一个很好的理由是, 输入和输出层对应于世界上已经出现或存在的明显事物, 可以存储为数据, 但是隐藏层中的值与现实世界无关, 或者与现实世界无关有数据。
从技术上讲, 隐藏层中的每个节点都代表来自输入数据的信息聚合;因此, 每个节点都会增加模型捕获数据之间交互的能力。节点越多, 可以从数据中实现更多的交互。
正向传播
让我们开始看看神经网络如何使用数据进行预测, 正向传播算法会对此加以注意。
为了理解正向传播的概念, 让我们重新回顾一下贷款公司的示例。为简化起见, 让我们仅考虑两个功能作为输入, 即年龄和退休状态, 退休状态是一个二进制数字(0-不退休和1-退休), 你可以根据此数字进行预测。

上图显示了一个40岁且未退休的客户。前向传播算法将通过网络/模型传递此信息, 以预测输出层。这些线将输入的每个节点连接到隐藏层的每个其他节点。每条线都有一个权重, 该权重指示该功能对连接到该特定线的隐藏节点的影响程度。
输入层和隐藏层之间共有四个权重。第一组权重从输入层的顶部节点连接到隐藏层的第一节点和第二节点;同样, 第二组权重从输入的底部节点连接到隐藏层的第一节点和第二节点。
请记住, 这些权重是深度学习的关键, 当你将神经网络拟合到数据时, 你就可以训练或更新这些权重。这些权重通常称为参数。
要预测隐藏层的顶部节点, 请考虑输入层中的每个节点乘以连接到该顶部节点的权重, 最后求和所有值, 得出40(40 * 1 + 0 * 1 = 40), 如上图所示。对隐藏层的底部节点重复相同的过程, 得到值40。最后, 对于输出层, 你遵循相同的过程并获得值0(40 * 1 + 40 *(-1)= 0)。该输出层预测值为零。
现在你可能想知道零值的相关性是什么, 那么你将贷款问题视为二进制分类, 其中输出为零表示贷款制裁, 而输出为1表示贷款禁止。
这几乎就是前向传播中发生的事情。你从输入层开始移动到隐藏层, 然后到输出层, 然后为你提供预测分数。你几乎总是使用加法运算, 在线性代数中, 此运算是点积运算。通常, 一次对单个数据点进行前向传播。
现在该看一下上述正向传播算法的代码了!
为此, 你将首先导入一个名为numpy的出色python库。
import numpy as np
接下来, 你将创建一个numpy input_data数组。
input_data = np.array([40, 0])
获得输入数据后, 现在将创建一个称为weights的字典, 该字典的关键字将包含隐藏层的node0和node1的变量名以及输出层的输出节点。字典的值将是参数(权重值)。
weights = {'node0':([1, 1]), 'node1':([1, -1]), 'output':([1, -1])}
让我们快速计算隐藏层的node0的值。首先, 将input_data与node0的权重相乘, 然后使用sum()函数获得标量值。
node0_value = (input_data * weights['node0']).sum()
你将对隐藏层的node1执行相同的操作。
node1_value = (input_data * weights['node1']).sum()
为简单起见, 让我们创建一个隐藏层值的numpy数组。
hidden_layer_values = np.array([node0_value, node1_value])
hidden_layer_values
array([40, 40])
最后, 将隐藏层的值乘以输出层的权重, 然后再次使用sum()函数获得预测。
output = (hidden_layer_values * weights['output']).sum()
让我们打印输出, 看看它是否与你期望的输出匹配!
output
0
激活函数
乘加过程只是神经网络工作方式的一半;还有更多!
为了利用最大的预测能力, 神经网络在隐藏层中使用激活函数。激活函数允许神经网络捕获数据中存在的非线性。
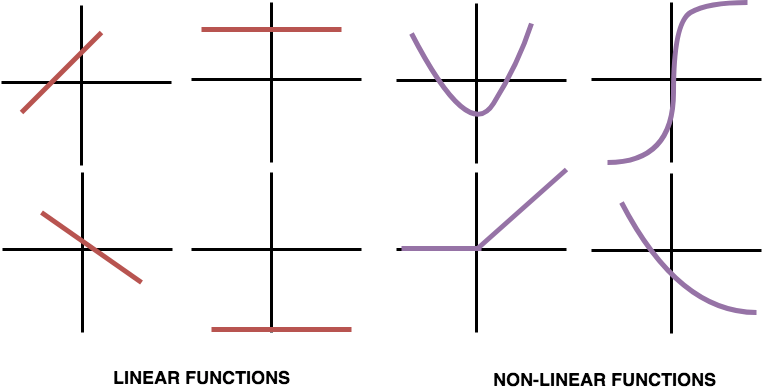
在神经网络中, 经常需要处理的数据不是线性可分离的, 并且要找到可以分隔数据点的决策边界, 你的网络中需要一些非线性。例如, 与之前拥有贷款记录的客户相比, 客户没有先前的贷款记录可能会对整体输出产生不同的影响。
如果数据中的关系不是直线或线性的, 则需要非线性激活函数来捕获非线性。将激活函数应用于进入节点的值, 然后将其转换为存储在该节点或节点输出中的值。
让我们将一个称为tanh的s形激活函数应用于隐藏层的节点。
node0_act = np.tanh(node0_value)
node1_act = np.tanh(node1_value)
hidden_layer_values_act = np.array([node0_act, node1_act])
hidden_layer_values_act
array([1., 1.])
你可以观察到hidden_layer_values和hidden_layer_values_act的差异。
让我们使用hidden_layer_values_act快速计算输出。
output = (hidden_layer_values_act * weights['output']).sum()
output
0.0
在当今时代, 一种称为”整流器线性单元”(ReLUifier)的激活函数已广泛应用于工业和研究领域。即使它有两个线性部分, 但通过多个隐藏层组合时, 它还是非常强大的。 ReLU从底部进行了一半整流, 如下图所示。

(资源)
现在, 你将在隐藏层节点上将ReLU用作激活函数, 并计算网络的输出。
def relu(input):
'''Define your relu activation function here'''
# Calculate the value for the output of the relu function: output
output = max(0, input)
# Return the value just calculated
return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node0']).sum()
node_0_output = relu(node_0_input)
# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node1']).sum()
node_1_output = relu(node_1_input)
# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])
# Calculate model output (do not apply relu)
model_output = (hidden_layer_outputs * weights['output']).sum()
# Print model output
print("Model's Output:", model_output)
Model's Output: 0
与上面的示例只有一个数据点(观测)相似, 你可以为多个观测或数据行实现同一网络。
深度学习(深度网络)
传统神经网络与利用神经网络的现代深度学习之间的重大区别在于, 不仅使用了一层, 而且还使用了许多连续的隐藏层。研究表明, 增加隐藏层的数量可以极大地提高性能, 从而使网络能够进行越来越多的交互。
在只有一个隐藏层和多个隐藏层的网络中, 工作情况保持不变。你可以像在上一个示例中一样使用一个隐藏层向前传播通过这些连续的隐藏层。

(资源)
让我们了解有关这些深度网络的一些基本事实!
- 深度学习网络能够在内部建立数据模式的表示形式, 这对于做出准确的预测至关重要;
- 初始层中的模式很简单, 但是当你遍历连续的隐藏层或深入网络时, 网络将开始学习越来越复杂的模式。
- 深度学习网络消除了对手工功能的需求。你无需创建更好的预测特征, 然后将其馈入深度学习网络, 网络本身会从数据中学习有意义的特征, 并使用它们进行预测。
- 深度学习也称为表示学习, 因为网络中的后续层将构建越来越复杂的数据表示, 直到你到达最终进行预测的最后一层。
从上图中, 让我们尝试了解网络试图捕获的表示形式。
上述网络的输入是人类的图像;你可以看到, 网络中的初始层捕获的是概念上比较简单的局部对比度模式, 例如垂直边缘, 水平, 对角边缘, 模糊区域等。一旦网络识别出这些对角线或水平线在哪里然后, 这些图层组合该信息以找到较大的图案, 例如眼睛, 鼻子, 嘴唇等。后面的图层可能组合这些图案以找到较大的抽象图案, 例如上图所示的脸。
好吧, 深度学习的妙处在于, 你不必明确地告诉网络寻找对角线, 或者图像是鼻子或嘴唇, 而不是在训练网络时, 神经网络就具有学会找到权重的权重相关模式以做出准确的预测。当然, 神经网络的学习过程是一个渐进的过程, 在该过程中, 网络要经过多次训练才能学会做出更好的预测。
多层神经网络中的正向传播
input_data = np.array([3, 5])
weights = {'node0_0':([2, 4]), 'node0_1':([4, -5]), 'node1_0':([-1, 2]), 'node1_1':([1, 2]), 'output':([2, 7])}

def predict_with_network(input_data):
# Calculate node 0 in the first hidden layer
node_0_0_input = (input_data* weights['node0_0']).sum()
node_0_0_output = relu(node_0_0_input)
# Calculate node 1 in the first hidden layer
node_0_1_input = (input_data* weights['node0_1']).sum()
node_0_1_output = relu(node_0_1_input)
# Put node values into array: hidden_0_outputs
hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
print("Hidden Layer 1 Output:", hidden_0_outputs)
# Calculate node 0 in the second hidden layer
node_1_0_input = (hidden_0_outputs* weights['node1_0']).sum()
node_1_0_output = relu(node_1_0_input)
# Calculate node 1 in the second hidden layer
node_1_1_input = (hidden_0_outputs* weights['node1_1']).sum()
node_1_1_output = relu(node_1_1_input)
# Put node values into array: hidden_1_outputs
hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
print("Hidden Layer 2 Output:", hidden_1_outputs)
# Calculate model output: model_output
model_output = (hidden_1_outputs * weights['output']).sum()
# Return model_output
return(model_output)
output = predict_with_network(input_data)
print("Model's Prediction:", output)
Hidden Layer 1 Output: [26 0]
Hidden Layer 2 Output: [ 0 26]
Model's Prediction: 182
提示:如果你到这里都无法理解, 那么你必须考虑阅读有关使用Keras用Python进行卷积神经网络的文章, 该文章教给你一种称为卷积神经网络的新术语, 不仅它还使用了称为Keras的深度学习框架, 与著名的图像数据集来对手写数字进行分类等等。
走得更远!
祝贺所有成功实现这一目标的人!
这篇文章试图让你对强大的神经网络, 神经网络如何使用正向传播算法学习以及如何使用名为numpy的python库实现正向传播进行直观了解, 并在深度神经网络上有了一些事实。
除了前向传播算法外, 神经网络中的学习还有更多附加组件, 因此可以更深入地研究神经网络, 以及如何使用这个神奇的网络进行预测, 可以考虑学习Python深度学习课程。本课程还将教你一个称为Keras的深度学习框架, 使用该框架只需几行代码就可以训练非常深的神经网络。
 srcmini
srcmini
评论前必须登录!
注册