10月是历史上最动荡的月份, 但这是持续的信号还是数据中的杂讯?
本文学习如何使用panda操作时间序列数据,使用Python模拟进行显著性检验,分析股市波动。
股票, 重要性测试和p-hacking。
“在过去的32年中, 10月是标准普尔500指数波动最大的月份, 而12月的波动最小。”
在本教程中, 我们将使用Python进行完整的分析和测试, 以确定该现象是否具有统计意义。
我们将使用熊猫的时间序列功能(例如”重采样”)将原始股票价格数据整理成一种使数据栩栩如生的格式。
然后, 我们将发现如何使用Python中的模拟代替繁琐的公式来进行假设检验。
最后, 我们将讨论统计分析中的一个主要问题, 多重比较偏差, 学习如何处理它并通过matplotlib直观地显示” p-Hacking”的效果。
我们的目标:
- 演示如何使用熊猫分析时间序列
- 了解如何构建假设检验
- 使用Python进行仿真以执行假设检验
- 显示考虑多重比较偏差的重要性
我们的数据:
我们将使用Daily S&P500数据进行此分析, 尤其是, 我们将使用1986年至2018年的原始每日收盘价(这很难找到, 因此我将其公开提供)。
这篇文章的灵感来自温顿, 尽管这里有32年的数据, 而我们有87年的数据, 但我们将在这里重现。
与熊猫争吵:
为了回答某些月份中出现的极端波动是否真的很重要并因此可能持续下去的问题, 我们需要将32年的价格数据转换为能够显示我们正在调查的现象的格式。
我们选择的格式将是平均每月波动率排名(AMVR)。
以下代码显示了我们如何将原始价格数据转换为这种格式。让我们开始吧!
首先是标准进口。 (matplotlib.patches使我们可以控制直方图中各个条的样式)
#standard imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
%matplotlib inline
使图表在Jupyter笔记本中显示全宽的一个不错的技巧:
#resize charts to fit screen if using Jupyter Notebook
plt.rcParams['figure.figsize']=[15, 5]
这是可选的-尝试一下, 看看会发生什么!
#plt.xkcd()
使用具有路径的read_csv方法导入数据, 在本例中为数据的url。我们还告诉它使用”日期”作为索引, 并尽可能地自动解析给定文本中的日期。
#Daily S&P500 data from 1986==>
url = "https://raw.githubusercontent.com/Patrick-David/Stocks_Significance_PHacking/master/spx.csv"
df = pd.read_csv(url, index_col='date', parse_dates=True)
#view raw S&P500 data
df.head()
| 关 | |
|---|---|
| 日期 | |
| 1986-01-02 | 209.59 |
| 1986-01-03 | 210.88 |
| 1986-01-06 | 210.65 |
| 1986-01-07 | 213.80 |
| 1986-01-08 | 207.97 |
这给了我们S&P500(SPX)未经调整的原始收盘价。现在我们需要将原始价格转换为每日%回报。为此, 我们有两个选择:
- 我们可以自然地记录价格。这将为真实的每日收益提供一个近似值。
- 我们可以使用pandas方法” pct_change()”直接计算每日百分比变化。
为了我们的目的, 我们将使用方法2, 因为熊猫可以立即处理此大小(超过8000个值)的数据集。我们还将通过删除第一个值(即” NaN”)来清理数据, 因为前一天没有价格变化。 pct_change()采用一个可选参数’periods’来更改周期移位。我们将其保留为默认值。
#To model returns we will use daily % change
daily_ret = df['close'].pct_change()
#drop the 1st value - nan
daily_ret.dropna(inplace=True)
#daily %change
daily_ret.head()
date
1986-01-03 0.006155
1986-01-06 -0.001091
1986-01-07 0.014954
1986-01-08 -0.027268
1986-01-09 -0.008944
Name: close, dtype: float64
下一步是获取这些每日百分比变化值, 并将其转换为”每月年度波动率”。下面的第一行代码显示我们可以只用一行代码执行此转换。这就是熊猫的力量!但是, 让我们依次解压每个步骤。
1.要获得mnthly_annu, 我们首先对每日收益使用”重新采样”方法。重采样允许我们更改数据周期的频率。它需要一个”频偏字符串”, 或者简单来说, 就是一个与所需新频率相对应的字母。他们包括:
- B工作日频率
- C自定义工作日频率
- D日历日频率
- W每周频率
- M月末频率
当我们想从每日收益重新采样到每月收益时, 我们将” M”作为参数。
2.我们需要做的第二件事是决定我们如何得出这个新的月度数字, 例如, 我们可以将每日价值相加, 相乘, 等等。对于我们的分析, 我们需要某种程度的波动性和标准度量。偏差效果很好, 因此我们将std()附加到我们的重新采样数据中以获得月波动率。
3.最后一步是将这一数字按年计算。我们可以简单地通过乘以12的平方根来实现, 其中12是一年中的周期数(月)。这为我们提供了我们所需的年度月度波动率值。
数据分析的最佳实践是在我们进行分析时可视化数据。因此, 让我们看一下我们的年度波动率数据。
下图清楚地显示了主要的市场事件, 例如黑色星期一和2008年金融危机。 matplotlib方法’axvspan’允许我们添加垂直线(axhspan是水平线的相应方法), 它以’xmin’和’xmax’作为参数, 它们指定创建的矩形的宽度, 因为我们的x轴是日期时间索引, 我们可以简单地输入要突出显示的年份。 alpha参数可调整块颜色的透明度, 因此我们仍然可以看到下面的图形。
mpatches属性允许我们创建一个自定义图例框。为此, 我们先定义颜色, alpha和所需文本的’labs’变量, 然后将其传递到plt.legend中的’handles’参数以呈现图例。
#use pandas to resample returns per month and take Standard Dev as measure of Volatility
#then annualize by multiplying by sqrt of number of periods (12)
mnthly_annu = daily_ret.resample('M').std()* np.sqrt(12)
print(mnthly_annu.head())
#we can see major market events show up in the volatility
plt.plot(mnthly_annu)
plt.axvspan('1987', '1989', color='r', alpha=.5)
plt.axvspan('2008', '2010', color='r', alpha=.5)
plt.title('Monthly Annualized vol - Black Monday and 2008 Financial Crisis highlighted')
labs = mpatches.Patch(color='red', alpha=.5, label="Black Monday & '08 Crash")
plt.legend(handles=[labs])
date
1986-01-31 0.033317
1986-02-28 0.023585
1986-03-31 0.027961
1986-04-30 0.037426
1986-05-31 0.027412
Freq: M, Name: close, dtype: float64
<matplotlib.legend.Legend at 0x280b1ee6908>

因此, 我们已经了解了熊猫中一种强大的方法, 即重新采样。现在, 让我们使用另一个” groupby”。我们需要从每月的年度波动率值到所需的AMVR指标。同样, 我们只需几行代码即可实现这一点。
1.首先, 我们对mnthly_annu值应用” groupby”方法。 Groupby需要一个参数, 该参数指定如何对数据进行分组。这可能是一个函数, 或者在我们的例子中是一个系列。我们传入” mnthly_annu.index.year”, 这只是mnthly_annu数据的datatime索引上的year属性。这将在我们的数据集中将32年中的每一年的月波动率值分组。
2.接下来, 我们应用”排名”方法, 该方法以升序对数据进行排序。
3.最后, 我们再次做同样的事情, 并在每个月的所有年度中平均。这为我们提供了最终的AMVR值!
#for each year rank each month based on volatility lowest=1 Highest=12
ranked = mnthly_annu.groupby(mnthly_annu.index.year).rank()
#average the ranks over all years for each month
final = ranked.groupby(ranked.index.month).mean()
final.describe()
count 12.000000
mean 6.450521
std 0.627458
min 5.218750
25% 6.031013
50% 6.491004
75% 6.704545
max 7.531250
Name: close, dtype: float64
这是我们最终的平均每月波动率排名。从数字上可以看到, 10月(10月)最高, 而12月(12月)最低。
#the final average results over 32 years
final
date
1 6.818182
2 6.666667
3 6.575758
4 7.303030
5 6.606061
6 6.030303
7 6.031250
8 5.875000
9 6.406250
10 7.531250
11 6.343750
12 5.218750
Name: close, dtype: float64
为我们的数据选择正确的可视化非常重要, 因为我们希望通过最具影响力的图表和绘图来讲述数据的故事。为了进行分析, 我们希望清楚地显示出最高的波动率和最低的波动率。为此, 我们将使用matplotlib的条形图并相应地进行注释和颜色以产生最大的影响。
1.通过用所需的条形索引b_plot(b_plot [9]), 我们可以设置颜色以突出显示最高和最低值。
2.要将AMVR值添加到其各自的栏中, 我们列举每个AMVR值(“最终”变量)并将结果四舍五入到小数点后两位。 ” i”和” v”代表”最终”变量的”索引”和”值”, 因此” i”的范围为1至12, “值”将AMVR值四舍五入到小数点后两位。我们在plt.text()中使用这些变量。 plt.txt()的第一个参数是标签的x轴位置, 因此我们为每个条传递” i”并偏移0.8以使其居中。第二个参数是”最终”值的字符串版本。
3.为了显示平均值, 我们使用axhline, 并使用” label”值在右上角添加图例。只需输入y轴值(即平均值), 然后添加样式即可。
这提供了我们正在研究的现象的最佳视觉效果。我们可以清楚地看到10月是最不稳定的月份, 而12月则是最少的月份。重要的是, 我们还可以看到, 从绝对意义上讲, 12月是更”极端”的价值。这对于下一部分的分析非常重要。
#plot results for ranked s&p 500 volatility
#clearly October has the highest AMVR
#and December has the lowest
#mean of 6.45 is plotted
b_plot = plt.bar(x=final.index, height=final)
b_plot[9].set_color('g')
b_plot[11].set_color('r')
for i, v in enumerate(round(final, 2)):
plt.text(i+.8, 1, str(v), color='black', fontweight='bold')
plt.axhline(final.mean(), ls='--', color='k', label=round(final.mean(), 2))
plt.title('Average Monthly Volatility Ranking S&P500 since 1986')
plt.legend()
plt.show()

这就是我们的数据, 现在进行假设检验…
假设检验:有什么问题?
假设测试是数据科学最基本的技术之一, 但它却是最令人生畏和误解的一种。这种恐惧的基础是《统计》第101条规定的教导方式, 我们被告知:
“执行t检验, 是单面还是双面检验?选择合适的检验统计数据, 例如Welch的t检验, 计算自由度, 计算t分数, 在表中查找临界值, 将临界值与t统计量进行比较……”
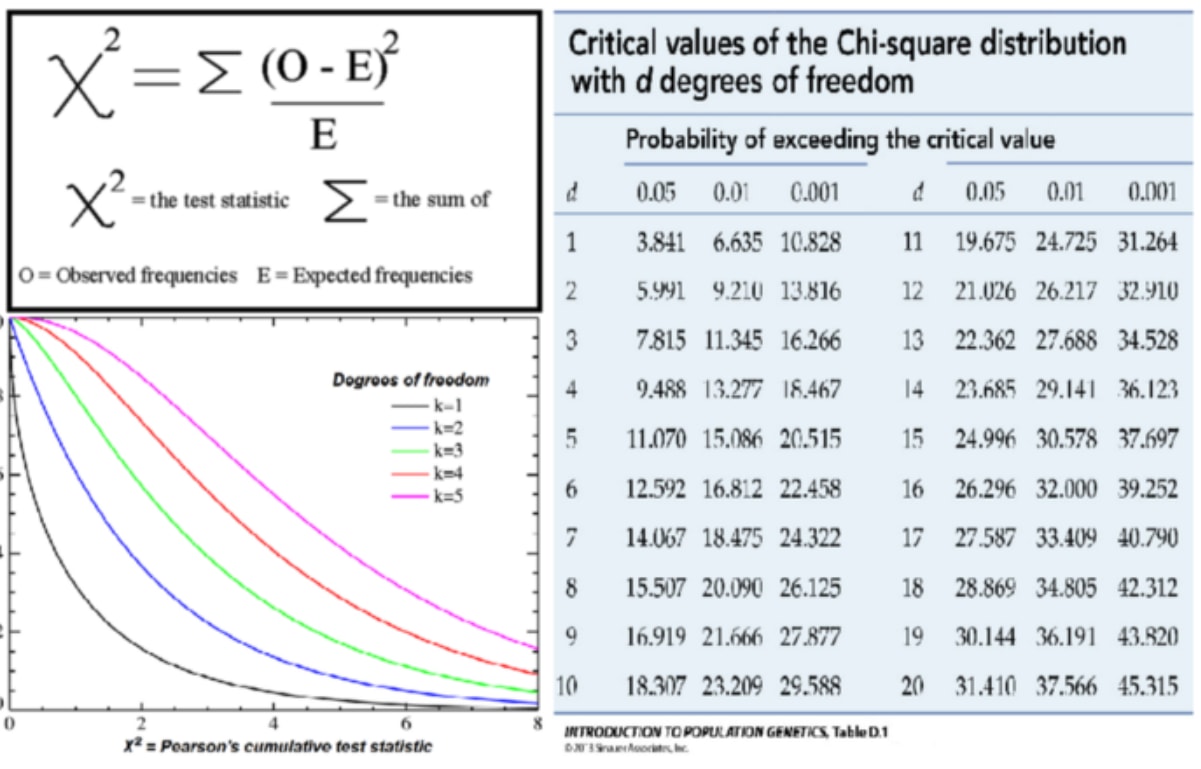
可以理解的是, 这导致了对进行何种测试以及如何进行测试的困惑。但是, 所有这些用于执行假设检验的经典统计技术都是在我们拥有很少的计算能力并且仅仅是用于计算p值的封闭形式分析解决方案的时候开发的, 仅此而已!但是, 由于其局限性(有时甚至是不透明的)假设, 因此需要为给定情况选择正确的公式, 这更加复杂。
但是很高兴!
有一个更好的办法。模拟。
为了了解模拟如何帮助我们, 让我们提醒自己什么是假设检验:
我们希望测试”我们的数据中观察到的效果是真实的还是偶然发生的”, 并且要执行此测试, 我们执行以下操作:
- 选择适当的”测试统计”:这只是一个衡量观察到的效果的数字。在本例中, 我们将从平均值中选择AMVR的绝对偏差。
- 构造一个零假设:这仅仅是数据的一个版本, 其中没有观察到的效果。在我们的例子中, 我们将反复对数据的标签进行重排(排列)。这样做的理由在下面详述。
- 计算p值:这是在空数据中看到观察到的效果的可能性, 换句话说, 是偶然的情况。我们通过对空数据进行重复仿真来做到这一点。在我们的案例中, 我们多次对数据的”日期”标签进行混洗, 并简单地计算通过多个模拟显示的测试统计数据的出现。
这是三个步骤的假设检验!无论我们正在测试什么现象, 问题始终是相同的:”观察到的效果是真实的, 还是由于偶然而产生的”
只有一个测试!艾伦·唐尼(Allen Downey)撰写的精彩博客, 提供了更多关于假设检验的详细信息
仿真的真正力量在于, 我们必须通过代码来明确我们的模型假设。当涉及到假设时, 古典技术可能是一个”黑匣子”。
下面的示例:左图以一定概率显示了真实数据和观察到的效果(绿色)。右图是我们模拟的空数据, 其中记录了偶然看到观察到的效果的时间(红色)。这是假设检验的基础, 看到观察到的对我们的空数据的影响的概率是多少。
假设检验的最关键部分是清楚我们要回答的问题。就我们而言, 我们在问:
“最大的价值会偶然发生吗?”
我们将最极端的值定义为AMVR与平均值的最大绝对偏差。这个问题构成了我们的原假设。
在我们的数据中, 最极端的值是12月的值(1.23)而不是10月的值(1.08), 因为我们正在寻找与均值的最大偏差, 而不仅仅是最大的波动率。
1.要获得绝对偏差, 我们只需从平均值中获取每个值并应用abs()函数。
2.通过使用sort_values()方法, 我们可以将结果从小到大排序。然后选择两个最大的值, 十月和十二月。
#take abs value move from the mean
#we see Dec and Oct are the biggest abs moves
fin = abs(final - final.mean())
print(fin.sort_values())
Oct_value = fin[10]
Dec_value = fin[12]
print('Extreme Dec value:', Dec_value)
print('Extreme Oct value:', Oct_value)
date
9 0.044271
11 0.106771
3 0.125237
5 0.155540
2 0.216146
1 0.367661
7 0.419271
6 0.420218
8 0.575521
4 0.852509
10 1.080729
12 1.231771
Name: close, dtype: float64
Extreme Dec value: 1.231770833333333
Extreme Oct value: 1.080729166666667
模拟
现在我们知道了我们要问的问题, 我们需要构建”空模型”。
这里有很多选项:
- 参数化模型。如果我们对数据分布有一个很好的想法, 或者只是简单地对其进行假设, 则可以使用”经典”假设检验技术, t检验, X², 单向方差分析等。这些模型可能是限制性的, 有些像黑盒如果研究人员不能完全理解他们的假设。
- 直接模拟。我们可以对数据生成过程进行假设并直接进行仿真。例如, 我们可以为要建模的财务数据指定一个ARMA时间序列模型, 并故意对其进行设计以使其没有季节性。对于我们的问题, 这可能是一个合理的选择。但是, 如果我们知道S&P500的数据生成过程, 那么我们已经变得很富有了!
- 通过重采样进行仿真。这就是我们将采取的方法。通过从现有数据集中随机抽样并改组标签, 我们可以使观察到的效果在我们数据中的所有标签(在我们的情况下, 标签是日期)之间同样可能, 从而提供所需的空数据集。
采样是一个很大的话题, 但是我们将专注于一种特定的技术, 即排列或混洗。
为了获得所需的空模型, 我们需要构建一个不存在季节性的数据集。如果null为真, 则数据中没有季节性, 并且观察到的效果仅仅是偶然的, 那么每个月(1月, 2月等)的标签都是没有意义的, 因此我们可以重复整理数据以建立什么经典统计将称为”零假设下检验统计的抽样分布”。这具有使所观察到的现象(12月的极端值)在所有月份中均等的可能性, 这正是我们的空模型所要求的。
为了证明现代计算能力具有多么强大的仿真技术, 此示例中的代码实际上将置换每日价格数据, 这需要更多的处理能力, 但在现代CPU上仍可在几秒钟内完成。
注意:在我们的情况下, 对每日或每月标签进行混排将为我们提供所需的空数据集。
Shuffle 'date' label to create null dataset
朱利安·西蒙(Julian Simon)是学习采样的重要资源。
注意:我们的测试构造方式等效于使用”经典”方法的双向测试, 例如Welch的t检验或ANOVA等, 因为我们对均值之上或之下的最大极限值感兴趣。 。
这些决定是设计选择, 我们拥有这种自由, 因为Null模型就是那个模型!这意味着我们可以在选择时指定其参数, 关键是要真正弄清楚我们要回答的问题。
因此, 我们想使用Python模拟大量数据以创建一个空数据集。为此, 我们将模拟1000套12个AMVR, 每次对”日期”标签进行排列以建立采样分布。该代码的输出包含在下面的p-hacking部分中。
1.首先, 我们定义一些容器来存储结果:我们将使用pd.Dataframe()和简单数组[]。
2.接下来, 我们定义一个计数器并将其设置为零, 然后开始进行1000次迭代的for循环以创建模拟数据。
3. for循环内的第一行采用原始的每日收益(从教程开始), 并使用pandas sample()方法。这将从每日收益数据中随机抽样给定次数。在我们的案例中, 我们有8191个数据点(32年中的252个交易日)。我们还使用reset_index()删除了索引, 因此我们可以添加一个新索引。我们需要执行此操作, 因为原始日期索引会与数据一起被改组, 而我们只想”改组”数据。
4.下一行通过将pd.bdate_range的等长长度重新分配给daily_ret_shuffle索引来向原始数据添加新的日期索引。我们使用bdate_range而不是date_range, 因为我们需要工作日(5, 周一至周五), 而不是每周7天。
5.现在我们已经生成了”混洗”数据, 我们将执行与开始构造AMVR值相同的数据整理工作。这就是接下来的三行代码。
6.现在我们有了模拟的AMVR值, 我们需要将它们附加到将存储所有1000次模拟运行的数据框中。 pd.concat获取当前数据帧, 并将每个后续数据帧追加到末尾。我们选择轴1, 所以我们得到数据列。
7. Maximonth是一个变量, 它仅存储每个模拟中的最大值(我们将在后面的分析中使用此值)。
8.由于我们的分析需要绝对的AMVR值, 因此接下来的三行代码将执行所有1000次AMVR运行并展平为一个大数组。然后, 我们取平均值, 并从该平均值中减去各个值, 最后取绝对值。
9.对于”仅最高”数据, 我们也做同样的事情。注意:这里我们使用列表而不是数据帧, 这意味着我们可以使用列表推导来计算每个最高值的Abs(AMVR)。
现在, 我们拥有完成分析所需的所有数据, 包括原始观测值和新的模拟数据集。
#as our Null is that no seasonality exists or alternatively that the month does not matter in terms of AMVR, #we can shuffle 'date' labels
#for simplicity, we will shuffle the 'daily' return data, which has the same effect as shuffling 'month' labels
#generate null data
new_df_sim = pd.DataFrame()
highest_only = []
count=0
n=1000
for i in range(n):
#sample same size as dataset, drop timestamp
daily_ret_shuffle = daily_ret.sample(8191).reset_index(drop=True)
#add new timestamp to shuffled data
daily_ret_shuffle.index = (pd.bdate_range(start='1986-1-3', periods=8191))
#then follow same data wrangling as before...
mnthly_annu = daily_ret_shuffle.resample('M').std()* np.sqrt(12)
ranked = mnthly_annu.groupby(mnthly_annu.index.year).rank()
sim_final = ranked.groupby(ranked.index.month).mean()
#add each of 1000 sims into df
new_df_sim = pd.concat([new_df_sim, sim_final], axis=1)
#also record just highest AMVR for each year (we will use this later for p-hacking explanation)
maxi_month = max(sim_final)
highest_only.append(maxi_month)
#calculate absolute deviation in AMVR from the mean
all_months = new_df_sim.values.flatten()
mu_all_months = all_months.mean()
abs_all_months = abs(all_months-mu_all_months)
#calculate absolute deviation in highest only AMVR from the mean
mu_highest = np.mean(highest_only)
abs_highest = [abs(x - mu_all_months) for x in highest_only]
骇客
这是有趣的一点。我们已经构建了一个假设进行测试, 我们通过改组数据的”日期”标签生成了模拟数据, 现在我们需要执行假设测试, 以发现观察到的结果与十二月的结果一样重要的概率, 因为零假设(无季节性)为真。
在进行测试之前, 请设定我们的期望。
在5%的显着性水平下, 看到至少一项显着的结果的概率是多少?
= 1-p(不重要)
= 1-(1–0.05)¹²
= 0.46
因此, 如果我们的null为真, 那么有46%的机会看到至少一个月会获得明显的效果。
现在让我们问一下, 对于每个单独的测试(将12个月的绝对AMVR与平均值进行比较), 我们期望在随机的非季节性数据中看到多少个有意义的值?
12 x 0.05 = 0.6
因此, 在显着性水平为0.05的情况下, 我们应该期望假阳性率为0.6。换句话说, 对于每个测试(具有无效数据), 将所有12个月的AMVR与平均值进行比较, 则0.6个月将显示出显着的结果。 (很明显, 我们不能少于1个月显示结果, 但是在重复测试下, 数学趋向于这个数字)。
在整个工作过程中, 我们一直强调必须对我们要回答的问题保持清楚。我们刚刚计算出的期望值的问题在于, 我们假设我们正在测试所有12个月的重大结果!这就是为什么看到至少一个假阳性的可能性如此之高, 高达46%的原因。
这是多重比较偏向的一个示例, 其中我们扩大了搜索空间并增加了找到重要结果的可能性。这是一个问题, 因为我们可能会滥用这种现象来挑选模型参数, 从而为我们提供”所需”的p值。
这是p-Hacking的本质
为了说明p-hacking的效果以及如何减少多重性, 我们需要了解以下两个问题之间的细微但重要的区别:
- “十二月偶然出现这种极端的可能性是多少。”
- “每个月偶然出现这种极端情况的概率是多少。”
模拟的优点在于其简单性。以下代码是我们计算p值以回答第一个问题所需的全部。我们使用所有12000 AMVR偏差(12个月x 1000次试验)简单地计算出数据集中有多少值大于观察到的12月值。我们获得4.4%的p值, 接近我们任意的5%截止值, 但仍然显着。
#count number of months in sim data where ave-vol-rank is >= Dec
#Note: we are using Dec not Oct, as Dec has highest absolute deviation from the mean
count=0
for i in abs_all_months:
if i> Dec_value:
count+=1
ans = count/len(abs_all_months)
print('p-value:', ans )
p-value: 0.04425
为了回答第二个问题并避免重复, 我们没有将我们的结果与所有12000个AMVR偏差的分布进行比较, 而是仅考虑了每个绝对AMVR 1000试验的最高值。这给出了23%的p值, 非常不重要!
#same again but just considering highest AMVR for each of 100 trials
count=0
for i in abs_highest:
if i> Dec_value:
count+=1
ans = count/len(abs_highest)
print('p-value:', ans )
p-value: 0.236
现在我们有了最终结果, 让我们绘制这些分布图以直观显示p-Hacking的影响和分析结果:
1.首先, 我们使用np.quantile()查找5%的显着性水平, 我们将使用axvline在较低的图上进行绘制。
2.接下来, 我们定义4个方框图。在这里, plt.subplots返回’fig’=我们的图形, 而’ax1, ax2, ax3, ax4’=代表4个子图的变量。
3. #plot 1显示第一列。在这里, 我们仅定义数据’abs_all_months’的直方图, 然后选择type =’bar’。对于较低的图, 我们将cumulative =’True’设置为” cdf”, 而不是” pdf”。 Bins定义了每个值要填充的条数, 对于我们的数据, 30是一个合理的数字。然后, 我们使用已经学习的技术(例如axvline)对图进行格式化, 以绘制显着性和观测值。
abs_all_months_95 = np.quantile(abs_all_months, .95)
abs_highest_95 = np.quantile(abs_highest, .95)
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, sharex='col', figsize=(20, 20))
#plot 1
ax1.hist(abs_all_months, histtype='bar', color='#42a5f5')
ax1.set_title('AMVR all months', fontsize=30)
ax1.set_ylabel('Frequency', fontsize=20)
ax3.hist(abs_all_months, density=1, histtype='bar', cumulative=True, bins=30, color='#42a5f5')
ax3.set_ylabel('Cumulative probability', fontsize=20)
ax1.axvline(Dec_value, color='b', label='Dec Result', lw=10)
ax3.axvline(Dec_value, color='b', lw=10)
ax3.axvline(abs_all_months_95, color='r', ls='--', label='5% Sig level', lw=10)
#plot2
ax2.hist(abs_highest, histtype='bar', color='g')
ax2.set_title('AMVR highest only', fontsize=30)
ax2.axvline(Dec_value, color='b', lw=10)
ax4.hist(abs_highest, density=1, histtype='bar', cumulative=True, bins=30, color='g')
ax4.axvline(Dec_value, color='b', lw=10)
ax4.axvline(abs_highest_95, color='r', ls='--', lw=10)
ax1.legend(fontsize=15)
ax3.legend(fontsize=15)
<matplotlib.legend.Legend at 0x280b4eb0b00>

左列是回答问题1的数据, 右列是问题2的数据。第一行是概率分布, 而下一行是CDF。红色虚线是我们任意确定的5%显着性水平。蓝线是12月AMVR的原始极端值为1.23。
左侧图显示原始的12月值在5%的水平上是显着的, 但仅仅是!但是, 当我们考虑多重比较偏差时, 在右侧图中, 显着性阈值从大约1.2(绝对AMVR)上升到大约1.6(参见红线)。
通过考虑多重比较偏差, 我们的12月值1.23不再重要!
考虑到我们要回答的特定问题并避免了多重比较偏差, 我们避免了p-hacking我们的模型, 并且避免了在没有模型时显示出明显的结果。
要进一步探索p-hack以及如何滥用它来讲述有关我们数据的特定故事, 请参阅FiveThirtyEight这款出色的交互式应用程序
结论
- 我们已经知道, 假设检验不是我们认为的可怕的大野兽。只需按照上述3个步骤为任何类型的数据或测试统计量构建模型。
- 我们已经证明, 提出正确的问题对于科学分析至关重要。措辞上的微小变化可能会导致完全不同的模型, 结果也大不相同。
- 希望更高级的Python功能的强大功能以及使你能够进行统计测试的能力现在已经显而易见!仅用几行代码, 我们就构造并测试了现实世界中的现象, 并能够得出可行的结论。
- 我们讨论了识别和纠正多重比较偏差并避免p-hacking陷阱的重要性, 并说明了看似有意义的结果如何变得不重要。
- 随着越来越多的”大数据”以及学术压力, 他们不得不发表具有”新”发现或具有政治压力以表明结果”重大”的研究论文, 因此对P黑客的诱惑日益增加。通过学会识别我们何时犯有罪并进行相应的纠正, 我们可以成为更好的研究人员, 并最终产生更准确, 因此更可行的科学成果!
作者注:我们的结果与最初的Winton研究略有不同, 部分原因是数据集有所不同(32年vs. 87年), 他们将10月作为关注月份, 而将12月作为关注月份。此外, 他们在”模拟数据”中使用了未公开的方法, 而我们通过代码明确了用于创建该数据的方法。在整个工作中, 我们已经做出了某些建模假设, 这些假设也已经明确, 可以在代码中看到。这些设计和建模选择是科学过程的一部分, 只要明确选择就可以进行分析。
如果你想了解有关Python中金融的更多信息, 请参加srcmini的Python金融入门课程。
在Twitter.com/pdquant上关注我, 了解更多!
 srcmini
srcmini
评论前必须登录!
注册