本文概述
数据科学领域取得了空前的进步。它将统计, 线性代数, 机器学习, 数据库等众多不同领域纳入其帐户, 并以最有意义的方式将它们合并。但是, 从本质上讲, 是什么使该领域成为最疯狂的领域之一? -强大的统计算法
一种非常原始的统计算法是线性回归。尽管它已经很老了, 但对于像你这样崭露头角的数据科学家来说, 它永远不会太老。理解线性回归工作原理的重要性对于推断一类称为广义线性模型的统计算法的发展非常重要。此外, 它还可以帮助你了解典型的统计/机器学习算法的其他方面, 例如-成本函数, 系数, 优化等。
就像本教程的标题所建议的那样, 你将在本教程中详细介绍线性回归。具体来说, 你将学习:
- 了解回归问题
- 提出关于回归问题的假设
- 什么是线性回归
- 成本函数
- 优化线性回归
- 为什么即使在神经网络领域也要理解仍然很重要
- Python案例研究
在深入研究线性回归背后的理论之前, 让我们对回归一词有一个清晰的了解。
了解回归问题
回归属于”监督学习”任务的类别, 其中用于预测/统计建模的数据集包含连续标签。但是, 让我们更数学地定义一个回归问题。
让我们考虑下图:
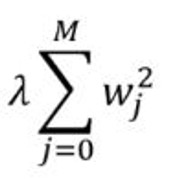
资料来源:吴安国的讲义
因此, 在上图中, X是与各种房屋的居住区域相对应的一组值(也被视为输入值的空间), y是各个房屋的价格, 但请注意, 这些值是由h预测的。 h是将X值映射到y的函数(通常称为预测变量)。由于历史原因, 此h称为假设函数。请记住, 此数据集仅具有(即, 各种房屋的起居区)特征, 为便于理解, 应将其视为玩具数据集。
注意, 这里的预测值实际上是连续的。因此, 给定训练集, 你的最终目标是学习函数$ h:\ mathcal {X} \ rightarrow \ mathcal {Y} $, 以便h(x)是y对应值的”良好”预测因子。此外, 请记住, X和Y都接受的值的域都是实数, 你可以这样定义:$ \ mathcal {X} = \ mathcal {Y} = \ mathbb {IR} $其中, $ \ mathbb {IR} $是所有实数的集合。
一对(x(i), y(i))被称为训练示例。你可以将训练集定义为{(x(i), y(i)); i = 1, …, m}(如果训练集包含m个实例, 并且数据集中只有一个特征x)。
那里有一些数学可以让你即使在最简单的事情上也不会出错。因此, 根据韩, 坎伯和裴恩所说,
“通常, 这些方法用于从一个或多个预测变量(独立变量)中预测响应变量(变量)的值, 其中变量是数字。” -数据挖掘:概念和技术(第3版)
就如此容易!
因此, 在理解典型的回归问题的过程中, 你还看到了如何为它定义假设。辉煌的去。你已经将心情定得完美!现在, 你将直接了解线性回归的原理。
线性回归-如何运作?
在详细介绍它之前, 先看看它是不是很好?好吧, 这可以追溯到18世纪。强大的卡尔·弗里德里希·高斯(Carl Friedrich Gauss)首先提出了最简单的统计回归形式, 但是对此有很多争论。让我们不要陷入那些。但是, 如果你有兴趣查看在高斯和Adrien-Marie Legendre之间发生的争执, 则可以单击此链接。
线性回归可能是统计和机器学习中最著名和最易理解的算法之一。线性回归是在统计领域开发的, 被研究为理解输入和输出数值变量之间关系的模型, 但是随着时间的流逝, 它已成为现代机器学习工具箱不可或缺的一部分。
让我们为其提供一个玩具数据集。你将使用相同的房价预测数据集进行调查, 但这一次具有两个功能。任务保持不变, 即预测房价。
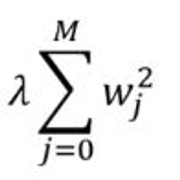
资料来源:吴安国的讲义
如前所述, x是二维的, 这意味着你的数据集包含两个要素。例如, x1(i)是训练集中第i个房屋的居住面积, x2(i)是其卧室数。
要执行回归, 必须确定表示h的方式。首先, 假设你决定将y近似为x的线性函数:
hθ(x)=θ0+θ1×1+θ2×2
在这里, θi是参数(也称为权重), 用于参数化从$ \ mathcal {X} $映射到$ \ mathcal {Y} $的线性函数的空间。从更简单的意义上讲, 这些参数用于将$ \ mathcal {X} $精确映射到$ \ mathcal {Y} $。但是为了使事情简单易懂, 你可以将θ下标放在hθ(x)中, 并将其简单写为h(x)。为了进一步简化符号, 你还将引入让x0 = 1(这是截距项)的约定, 以便
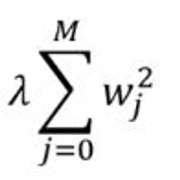
在上面的右手边, 你将θ和x都视为向量, 这里n是输入实例的数量(不计x0)。
但是, 此时提出的主要问题是如何选择或学习参数θ?你无法更改输入实例以预测价格。你只有这些θ参数可以调整/调整。
一种突出的方法似乎是使h(x)接近y, 至少对于你的训练示例而言。为了更正式地理解这一点, 让我们尝试定义一个函数, 该函数针对θ的每个值确定h(x(i))与相应y(i)的接近程度。该函数应如下所示:
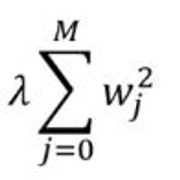
资料来源:StackOverflow
要了解采用平方值而不是绝对值的原因, 请将此平方项视为将来训练回归模型时要执行的操作的一项优势。但是, 如果你想更深入, 请自助。
你刚刚看到了数据科学/机器学习/统计领域最重要的公式之一。它称为成本函数。
这是一个重要的推导, 因为它不仅催生了线性回归的下一个演变(普通最小二乘), 而且为整个线性建模算法的类别奠定了基础(请记住, 你遇到了一个称为广义线性模型的术语)。
重要的是要注意, 线性回归通常可以分为两种基本形式:
- 简单线性回归(SLR)仅处理两个变量(你第一次看到的变量)
- 多线性回归(MLR), 它处理两个以上的变量(你刚刚看到的一个)
这些事情非常简单, 但是经常会引起混乱。
你已经奠定了线性回归的基础。现在, 你将学习更多有关估计上一节中看到的参数的方法。参数的这种估计本质上称为线性回归训练。现在, 有很多方法可以训练线性回归模型, 其中最流行的是普通最小二乘(OLS)。因此, 最好将使用OLS训练的线性回归模型作为普通最小二乘线性回归或仅作为最小二乘回归。
注意, 此处的参数在此也称为模型系数。
优化线性回归模型-各种方法
学习/训练线性回归模型实质上意味着用你拥有的数据估计表示中使用的系数/参数的值。
在本节中, 你将简要介绍一些用于准备线性回归模型的技术。
最小二乘回归
你在上一节中留下了选择θ的概念, 以便最小化J(θ)。为此, 我们使用一种搜索算法, 该算法从θ的”初始猜测”开始, 然后迭代地更改θ以使J(θ)变小, 直到希望收敛到使J(θ)最小的θ值为止。具体来说, 让我们考虑梯度下降算法, 该算法从某个初始θ开始, 然后重复执行更新:
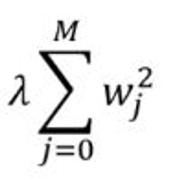
资料来源:吴安国的讲义
(对于j = 0, …, n的所有值同时执行该更新。)这里, α称为学习率。这是一种非常自然的算法, 反复朝着J的最大减小方向迈出了一步。这个项α有效地控制了算法向J的减小的陡峭程度。它可以用以下图形表示:

资料来源:ml-cheatsheet
从直觉上讲, 以上公式表示θj参数发生的微小变化, 以及它如何影响θj的初始值。但是仔细看, 这里有一个偏导数要处理。整个推导过程不在本教程的讨论范围之内。
请注意, 对于一个培训示例, 这给出了更新规则:
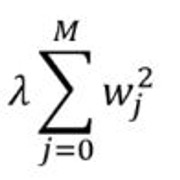
资料来源:ml-cheatsheet
该规则称为LMS更新规则(LMS代表”最小均方”), 也称为Widrow-Hoff学习规则。
让我们在OLS的上下文中总结一些事情。
“普通最小二乘程序试图使残差平方和最小化。这意味着, 给定一条通过数据的回归线, 我们可以计算出每个数据点到回归线的距离, 将其平方并求和, 然后将所有平方误差求和这是普通最小二乘试图最小化的数量。” -杰森·布朗利
梯度下降的优化
在以前的训练规则中, 你已经有了在这种情况下如何结合梯度下降的概念。本质上, 梯度下降是通过迭代最小化模型对训练数据的误差来优化系数值的过程。
简而言之, 它以每个系数的随机值开始。为每对输入和输出值计算平方误差的总和。学习率用作比例因子, 并且朝着最小化误差的方向更新系数。重复该过程, 直到获得最小平方和误差或无法进一步改善。
术语α(学习率)在这里非常重要, 因为它确定了在过程的每次迭代中采取的改进步骤的大小。
现在通常有两种梯度下降方式:
- 在每个步骤的整个训练集中查看每个示例的方法, 称为批量梯度下降。
- 该方法是你反复遍历训练集的方法, 并且每次遇到训练示例时, 都仅根据该单个训练示例的误差梯度来更新参数。此算法称为随机梯度下降(也称为增量梯度下降)。
这就是本教程的梯度下降。现在, 你看一下优化线性回归模型的另一种方法, 即正则化。
正则化
srcmini已经有一篇很好的关于正则化的介绍性文章。你可能需要先检查一下, 然后再继续进行。
通常, 正则化方法通过惩罚具有极大值的特征的系数来工作, 从而尝试减小误差。它不仅导致错误率提高, 而且降低了模型复杂度。当你处理具有大量特征的数据集, 并且基线模型无法区分特征的重要性时, 这特别有用(不是数据集中的所有特征都同样重要, 对吧?)。
线性回归的正则化程序有两种变体:
拉索回归:增加一个惩罚项, 它等于系数幅度的绝对值(也称为L1正则化)。惩罚条款如下:
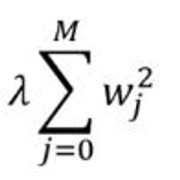
其中
- $ \ lambda $是为控制错误改善速度而增加的常数(学习率)
- 数据集具有(M + 1)个特征, 因此它的范围是0到M。wj是权重/系数。
岭回归:添加一个惩罚项, 它等于系数幅度的平方(也称为L2正则化)。惩罚条款如下:
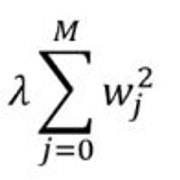
仍然值得花时间学习线性回归吗?
不是吗你已经看到了线性回归如何优雅地引入了一些机器学习的最关键概念, 例如成本函数, 优化, 变量关系以及什么不?即使你正在构建神经网络, 所有这些事情也至关重要。在某些地方适用性可能有所不同, 但总体概念仍然完全相同。因此, 如果不了解这些基本知识, 你将无法推理神经网络表现不佳的原因。
此外, 推导变量之间关系的简单概念催生了许多概念, 最重要的是, 它创建了一个全新的算法家族-广义线性模型。因此, 对于有抱负的数据科学/机器学习/人工智能从业者来说, 这种算法是不容忽视的。现在你已经了解了!
不, 你现在将自己在Python中实现一个简单的线性回归。应该很好玩!
Python案例研究
首先, 对于本案例研究, 你将使用Python的Statsmodel库。它是一个非常流行的库, 它提供用于估计许多不同统计模型以及进行统计测试和统计数据探索的类和功能。对于数据, 你将使用著名的Boston House数据集。此数据集附带强大的scikit-learn, 因此你无需单独下载。
让我们通过导入statsmodels库和数据集来开始案例研究:
import statsmodels.api as sm
from sklearn import datasets
data = datasets.load_boston()
Scikit-learn提供了数据集的方便描述, 可以通过以下方式轻松查看:
print (data.DESCR)
Boston House Prices dataset
===========================
Notes
------
Data Set Characteristics:
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive
:Median Value (attribute 14) is usually the target
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25, 000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10, 000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management, vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
**References**
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan, R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
- many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)
现在, 在应用线性回归之前, 你将必须准备数据并隔离数据集的特征和标签。在这种情况下, MEDV(房屋中位数)为标签。你可以使用feature_names属性访问数据集的要素。
这里有些熊猫知识会派上用场。如果你正在寻找刷新基本熊猫概念的方法, 那么这份备忘单是必看的。
# Pandas and NumPy import
import numpy as np
import pandas as pd
# Set the features
df = pd.DataFrame(data.data, columns=data.feature_names)
# Set the target
target = pd.DataFrame(data.target, columns=["MEDV"])
此时, 在将线性回归应用于数据之前, 你需要考虑一些重要事项。你本可以在本教程的前面进行研究, 但是在特定的时间点研究这些因素将有助于你获得真实的感觉。
- 线性假设:最好使用线性回归来捕获输入变量和输出之间的关系。为了做到这一点, 线性回归假定此关系是线性的(可能并非一直如此)。但是你始终可以转换数据, 以保持线性关系。例如, 如果你的数据具有指数关系, 则可以应用对数转换以使关系线性化。
- 特征之间的共线性:共线性是一种以数学方式计算数据集特征重要性的度量。当你拥有一个要素之间非常相关的数据集时, 线性回归无法正确地近似关系, 并且往往会过拟合。因此, 在应用线性回归之前, 检测出高度相关的特征并将其删除是非常有效的。如果你想了解更多有关此的信息, 请随时检查此出色的Kaggle内核。
现在开始动手做吧。为了简单起见, 你只需支付RM, 即现在的平均客房数量。请注意, 默认情况下, Statsmodels不会添加常数项(调用因子θ0)。让我们首先来看一下回归模型中没有常数项的情况:
X = df["RM"]
y = target["MEDV"]
# Fit and make the predictions by the model
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
# Print out the statistics
model.summary()

这是什么输出!当你第一次看到它时, 它太大了以至于无法理解。让我们逐步了解最关键的点:
- 你应该在这里进行的第一个观察是, 你正在使用OLS方法来训练线性回归模型。
- 有一个对应于R-Squared的值。 R平方是模型的”解释的差异百分比”。即, R平方是误差的方差小于因变量的方差的分数。 R平方值的范围是0到1, 通常表示为从0%到100%的百分比。 R平方将基于自变量的运动为你提供因变量运动之间的关系估计。它不会告诉你所选模型的好坏, 也不会告诉你数据和预测是否有偏差。较高或较低的R平方不一定是好是坏, 因为它不能传达模型的可靠性, 也不能传达你是否选择了正确的回归。对于一个好的模型, 你可以得到一个较低的R平方, 而对于一个不合适的模型, 则可以得到一个较高的R平方, 反之亦然。
- 系数(系数)为3.634, 意味着如果RM变量增加1, 则MEDV的预测值将增加3.634。
- RM有95%的置信区间, 这意味着模型以95%的置信度预测RM的值在3.548至3.759之间。
这些是你暂时应该注意的最重要的点(你也可以忽略该警告)。
常数项可以轻松地添加到线性回归模型中。你可以通过X = sm.add_constant(X)来实现(X是包含输入(独立变量)的数据框的名称。
X = sm.add_constant(X)
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
model.summary()
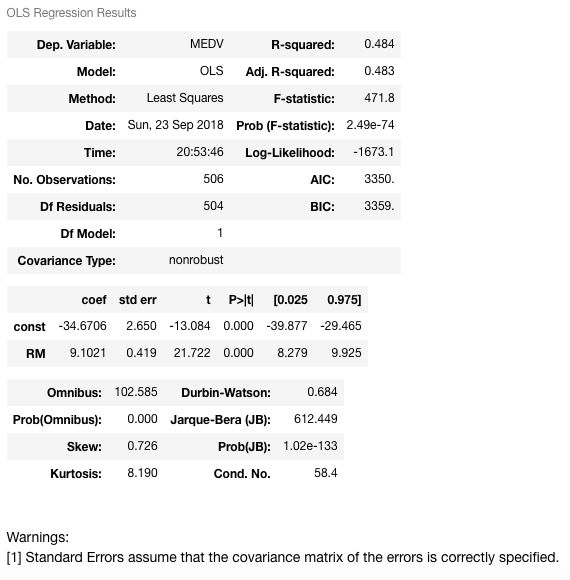
可以清楚地看到, 常数项的加法直接影响系数项。没有常数项, 你的模型正在通过原点, 但是现在你的截距为-34.67。现在, RM预测变量的斜率也从3.634更改为9.1021(RM系数)。
现在, 你将使用一个具有多个变量的回归模型拟合-你将加上LSTAT(较低地位人口的百分比)以及RM变量。模型训练(拟合)过程与之前的过程完全相同:
X = df[["RM", "LSTAT"]]
y = target["MEDV"]
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
model.summary()
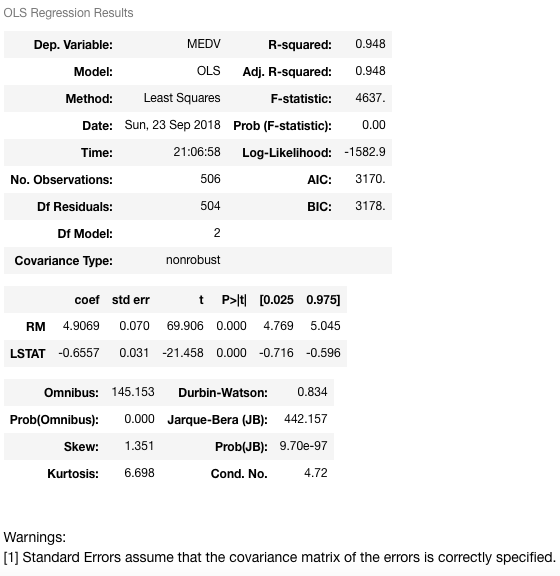
现在让我们解释一下:
该模型具有更高的R平方值480.948, 这实际上意味着该模型捕获了因变量中94.8%的方差。现在, 让我们尝试找出两个变量RM和LSTAT与房屋中位数之间的关系。当RM增加1时, MEDV将增加4.9069, 而当LSTAT增加1时, MEDV将减少0.6557。这表明RM和LSTAT在预测(或估计)房屋中位数方面具有统计学意义。
你也可以用简单的英语解释这种关系:
- 房间数量少的房屋价格可能很低。
- 在人口状况较低的地区, 房价可能很低。
现在更有意义!是不是
这是Statsmodels中单线性回归和多元线性回归的示例。你的作业将是使用其他功能来调查和解释结果。
接下来, 让我们看看如何使用自己的scikit-learn实现线性回归。你已经导入了数据集, 但是必须导入linear_model类。
from sklearn import linear_model
X = df
y = target["MEDV"]
lm = linear_model.LinearRegression()
model = lm.fit(X, y)
模型训练完成。此sklearn实现也使用OLS。让我们对前五个样本的MEDV值进行一些预测。
predictions = lm.predict(X)
print(predictions[0:5])
[30.00821269 25.0298606 30.5702317 28.60814055 27.94288232]
如果你想知道模型的更多详细信息(例如R平方, 系数等), 则可以轻松做到。
lm.score(X, y)
0.7406077428649427
lm.coef_
array([-1.07170557e-01, 4.63952195e-02, 2.08602395e-02, 2.68856140e+00, -1.77957587e+01, 3.80475246e+00, 7.51061703e-04, -1.47575880e+00, 3.05655038e-01, -1.23293463e-02, -9.53463555e-01, 9.39251272e-03, -5.25466633e-01])
包起来!
美丽!你已经做到了。涵盖最简单, 最基础的算法之一并不是那么容易, 但是你做得很好。你不仅熟悉简单的线性回归, 还研究了机器学习的许多基本方面, 术语和因素。你还使用Python进行了深入的案例研究。
本教程也可以被视为你从头开始实施线性回归的动力。如果有人想真正做到, 请按照以下简短步骤进行操作:
- 计算数据的均值和方差
- 计算协方差
- 估计系数
- 作出预测
以下是用于准备本教程的一些参考资料:
- Coursera的机器学习课程(由伟大的Andrew Ng教授)
- 从零开始实施线性回归
- 统计学习的要素
- Python中的简单多元线性回归(作者:Adi Bronshtein)
如果你想了解有关线性分类器的更多信息, 请参加srcmini的Python线性分类器课程。
 srcmini
srcmini
评论前必须登录!
注册