个性化阅读
专注于IT技术分析
        找回密码
当前位置：srcmini > R编程 > 正文

使用R进行时间序列分析

2020-04-08 20:29:09 分类：R编程 / 人工智能 / 机器学习 / 深度学习 阅读(1011) 评论(0)

本文概述

时间序列是度量, 或者它是在常规时间内测量的度量标准, 称为时间序列。时间序列分析的例子包括财务, 股票价格, 天气数据, 效用研究等等。

时间序列模型可以通过以下方式完成：

  • 对产生观察数据的潜在力和结构的理解已经完成。
  • 开始拟合模型, 也开始进行预测, 监视甚至反馈和前馈控制。

在本教程中, 将为你提供固定和非固定时间序列模型的概述。将显示如何通过计算其ACF和PACF来识别时间序列。这些功能的图形可以判断时间序列的平稳性。我们可以通过微分使非平稳序列平稳。了解了序列的性质, 现在可以很容易地从该序列所遵循的模型中预测未来的价值。可以在R的TSA软件包中找到的真实数据的说明也将是本教程的一部分。

假设$ X $是索引为时间的随机变量(通常用$ t $表示), 则\ textbf {N} \ right \} $中的观测值$ \ left \ {x_t, \, t \称为时间序列。 $ \ textbf {N} $是整数集, 在这里被视为时间索引集。 $ N $也可以是时间戳记。平稳性是时间序列模型中的一个关键假设, 它暗示序列中的同质性, 即无论时间如何, 序列的行为都相似, 这意味着其统计属性不会随时间变化。平稳性有两种形式：强形式和周形式。

定义1

如果固定的过程$ \ left \ {x_t, \, t \ in \ textbf {N} \ right \} $中的时间或时间尺度偏移后其统计分布保持不变, 则称其为严格或强烈静止的。由于随机过程的分布是由有限维分布函数定义的, 因此我们可以制定严格平稳性的替代定义。如果在每个$ n $中, 每次选择$ t_1, t_2, \ ldots, t_n \ in在\ textbf {N} $中并且每次滞后$ k $使得$ t_ {i + k} \ in \ textbf {N } $, $ n $维随机向量$(X_ {t_1 + k}, X_ {t_2 + k}, \ ldots, X_ {t_n + k})$具有与向量$(X_ {t_1 }, X_ {t_2}, \ ldots, X_ {t_n})$, 则该过程严格是固定的。那是为$ h $和$ x_i $

\ begin {align *} P(X_ {t_1} \ leq x_1, X_ {t_2} \ leq x_2, \ ldots, X_ {t_k} \ leq x_k)＆= F(x_ {t_1}, x_ {t_2}, \ ldots, x_ {t_k})\\＆= F(x_ {h + t_1}, x_ {h + t_2}, \ ldots, x_ {h + t_k})\\＆= P(X_ {h + t-1 } \ leq x_1, X_ {h + t_2} \ leq x_2, \ ldots, X_ {h + t_k} \ leq x_k)\ end {align *}

对于任何时移$ h $和观测值$ x_j $。如果$ \ left \ {X-t, \, t \ in \ textbf {N} \ right \} $是严格固定的, 则$ X_t $的边际分布与$ t $无关。而且, $(X_ {t_1}, X_ {t_2})$的二维分布与$ t_1 $和$ t_2 $的绝对位置无关, 只有距离$ t_1-t_2 $才重要。结果, 均值函数$ E(X)$是常数, 协方差$ Cov(X_t, X_ {tk})$仅是$ k $的函数, 而不是$ k $和$的绝对位置t $。在较高阶的时刻, 例如三阶矩, 如果将恒定的时移添加到$ s, t, u $, 则$ E [X_uX_tX_v] $保持不变。

定义2

如果单变量时间序列$ X_t $的均值, 方差和协方差与时间无关, 则它是平稳的。因此, 如果$ X_t $是为$ t = 1, 2, 3, \ ldots, n $和$ t = 0, -1, -2, -3, \ ldots $, 则$ X_t $在数学上是弱固定的, 如果

\\开始{align}(i)＆E [X_t] = \ mu \\(ii)＆E \ left [(X- \ mu)^ 2 \ right] = Var(X_t)= \ gamma(0)= \ sigma ^ 2 \\(iii)＆E \ left [(X_t- \ mu)(X_ {tk}-\ mu)\ right] = Cov(X_t, X_ {tk})= \ gamma(k)\ end {对齐}

前两个条件($(i)$和$(ii)$)要求流程分别具有恒定的均值和方差, 而$(iii)$要求任何两个值之间的协方差(正式称为协方差函数)仅取决于在这两个值之间的时间间隔$ k $上, 而不是在时间点$ t $上。

如果一个过程是具有有限第二矩的高斯过程, 则弱平稳性等于强平稳性。仅在必要的时刻存在时, 斯特里克平稳性意味着较弱的平稳性。强烈的平稳性还需要分配假设。强形式通常被认为过于严格, 因此, 你将主要关注弱平稳性, 有时也称为协方差平稳性, 广义平稳性或二阶平稳性。

平稳性和随机时间序列(随机过程)

观测值围绕恒定均值波动, 具有连续方差且随机独立的时间序列是随机时间序列。这样的时间序列没有任何模式：

  • 观察结果不倾向于向上或向下
  • 方差不会随时间增加或减少
  • 在某些时期, 观察结果往往不大

平稳随机模型的一个例子可以写成

$$ X_t = \ mu + \ varepsilon_t $$, 其中$ \ mu $是恒定平均值, 使得$ E [X_t] = \ mu $和$ \ varepsilon_t $是假设为零均值, 恒定方差且为独立(也称为白噪声)。

模拟随机时间序列

# purely random process with mean 0 and standard deviation 1.5
eps <- rnorm(100, mean = 0, sd = 1)
mu <- 2 # the constant mean
# The process
X_t <- mu + eps

# plotting the time series
ts.plot(X_t, main = "Example of (random) stationary time series", ylab = expression(X[t]))

模拟过程围绕恒定平均值$ \ mu = 2 $波动。

自协方差功能

平稳随机过程的理论自协方差函数(ACF)是评估时间序列性质的重要工具。设$ X_t $是一个固定的随机过程, 均值$ \ mu $, 方差$ \ sigma ^ 2 $。滞后$ k $, $ \ gamma(k)$的ACF为$$ \ gamma(k)= \ frac {\ gamma(k)} {\ gamma(0)} = \ frac {\ gamma(k) } {\ sigma ^ 2} $$

ACF函数是自协方差的归一化度量, 并具有多个属性。

ACF的属性

  1. $ \ rho(0)= 1 $
  2. ACF是滞后的偶数函数。这意味着$ \ rho(k)= \ rho(-k)$
  3. $ | \ rho(-k)| \ leq $ 1

下图表示上述过程的ACF。

# Auto-covariance function of the simulated stationary random time series
acf(X_t, main = "Auto-covariance function of X")

注1.缺乏唯一性是ACF的特征。即使给定的随机数具有唯一的协方差结构, 相反的情况通常也不成立：使用相同的ACF可以找到多个随机过程。这会导致规格问题, 请参见[@jenkinsd]。

注2：一个非常特殊的矩阵是通过平稳过程的自相关函数获得的。它称为Toeplitz矩阵。它是阶数为$ m = t-k $的方差和协方差矩阵(滞后, 包括与滞后$ m-1 $的自相关), 因此它是对角的, 对称的, 正定的。

\ begin {equation} \ begin {pmatrix} 1＆\ rho(1)＆\ rho(2)＆\ cdots＆\ rho(m-1)\\ \ rho(1)＆1＆\ rho(1)＆ \ cdots＆\ rho(m-2)\\ \ cdots＆\ cdots＆\ cdots＆\ cdots＆\ cdots \\ \ rho(m-1)＆\ rho(m-2)＆\ cdots＆\ rho( 1)＆1 \ end {pmatrix} \ end {equation}

纯随机过程或白噪声

如果随机变量$ Z_t $形成一系列相互独立且分布均匀的变量(i.i.d.), 则离散过程$ \ left \ {Z_t \ right \} $称为纯随机过程。该定义暗示过程具有恒定的均值和方差。

$$ \ gamma(k)= cov(Z_t, Z_ {t + k})= 0, \ quad \ forall k \ in -3, -2, -1, 0, 1, 2, 3, \ ldots $$鉴于均值和自协方差函数(acvf)不依赖于时间, 该过程是二阶平稳的。

随机游走过程

如果$ X_t = X_ {t-1} + Z_t $, 则过程$ \ left \ {X_t \ right \} $被称为随机游走过程, 其中$ Z_t $是纯随机过程, 均值$ \ mu $和方差$ \ sigma ^ 2_Z $。该过程通常说明为$ t = 0 $, 我们有$ X_1 = Z_0 $, 这意味着$ X_0 = 0 $。我们有

\ begin {align *} X_1＆= X_0 + Z_1, \ quad \ text {at} t = 1 \\ X_2＆= X_1 + Z_2 = X_0 + Z_1 + Z_2, \ quad \ text {at} t = 2 \\ X_3 ＆= X_2 + Z_3 = X_0 + Z_1 + Z_2 + Z_3, \ quad \ text {at} t = 3 \\＆＆\ cdots \\ X_t＆= X_0 + \ sum_ {i = 1} ^ tZ_i \ end {align *}

此过程的一阶矩(或期望值)等于$$ E [X_t] = X_0 + \ sum_ {i = 1} ^ tE [Z_i] = X_0 + t \ mu_z = t \ mu_z $$和方差$$ Var(X_t)= t \ sigma ^ 2_Z $$注意, 均值和方差随时间变化, 因此, 过程为\ textbf {non-stationary}。表现为随机游走的时间序列的一个示例是股价。

随机游走过程模拟

# seed X_0 = 0
X <- 0

# purely random process with mean 0 and standard deviation 1.5
Z <- rnorm(100, mean = 0.5, sd = 1.5)

# the process
for (i in 2:length(Z)){
  X[i] <- X[i-1] + Z[i]
}

# process plotting
ts.plot(X, main = "Random walk process")

区别

求差是使时间序列数据保持平稳的最常用方法。这是一种特殊类型的过滤, 在消除趋势中尤其重要。对于季节性数据, 一阶差分数据通常足以获得均值的平​​稳性。令$ X_t = \ left \ {X_1, X_2, \ ldots, X_n \ right \} $为非平稳时间序列。固定式领带为

$$ \ Delta X_ {t + 1} = X_ {t + 1} -X_t \ quad \ text {or} \, \ Delta X_ {t} = X_t-X_ {t-1} $$, 简称为一阶差异。如果需要二阶差分, 则可以使用运算符$ \ Delta ^ 2 $是一阶差分的差分

$$ \ Delta ^ 2X_ {t + 2} = \ Delta X_ {t + 2}-\ Delta X_ {t + 1} $$

# differencing and plotting of the random walk process
ts.plot(diff(X))

你知道所产生的一阶差围绕恒定均值0波动。这是因为在数学上

$$ \ Delta X_ {t + 1} = X_ {t + 1} -X_t = Z_t $$这是平稳的, 因为它是一个纯随机过程, 具有恒定的均值和恒定的方差。

order$ q $的移动平均线：MA($ q $)

令$ \ left \ {Z_t \ right \} $是一个纯随机过程, 均值为零, 方差为$ \ sigma ^ 2_Z $。如果该过程称为＃q＃的移动均线, 则

$$ X_t = \ beta_0Z_t- \ beta_1Z_ {t-1}-\ cdots- \ beta_q Z_ {t-q} $$其中$ \ beta_i, \, i = 1, 2, \ ldots, q $是常数。通常按比例缩放随机变量$ Z_t, \, t \ in \ textbf {N} $, 以便$ \ beta_0 = 1 $

一阶MA的仿真

# purely random process with mean 0 and standard deviation 1.5 (arbitrary choice)
Z <- rnorm(100, mean = 0, sd = 1.5)

# process simulation
X <- c()
for (i in 2:length(Z)) {
  X[i] <- Z[i] - 0.45*Z[i-1]
}

# process plotting
ts.plot(X, main = "Moving Average or order 1 process")

对于MA(1)过程, 可以如下验证这三个条件：

\ begin {align} E [X_t]＆= 0 \\ Var(X_t)＆= E [X_t ^ 2]-0 = E \ left [Z_t ^ 2-2 \ beta Z_tZ_ {t-1} + \ beta ^ 2Z_ {t-1} ^ 2 \ right] = \ sigma ^ 2_Z + \ beta ^ 2 \ sigma ^ 2_Z \\ \ gamma(k)＆= cov(X_t, X_ {t + k})= E [X_tX_ {t + k}]-E [X_t] E [X_ {t + k}] = E [X_tX_ {t + k}] \\＆= E \ left [(Z_t- \ beta Z_ {t-1})(Z_ {t + k}-\ beta Z_ {t-1 + k})\ right] \\＆= E \ left [Z_tZ_ {t + k}-\ beta Z_tZ_ {t-1 + k}-\ beta Z_ { t-1} Z_ {t + k} + \ beta ^ 2 Z_ {t-1} Z_ {t-1 + k} \ right] \\ \ end {align}

对于$ k = 0, \, \ gamma(0)= Var(X_t)= \ sigma ^ 2_Z(1+ \ beta ^ 2)$

对于$ k = 1, \, \伽玛(1)= E \左[Z_tZ_ {t + 1}-\ beta Z_t ^ 2-\ beta Z_ {t-1} Z_ {t + 1} + \ beta ^ 2 Z_ {t-1} Z_ {t} \ right] =-\ beta \ sigma ^ 2_Z $

并且对于$ k> 1, \, \ gamma(k)= 0. $

因此, 当位移大于一个周期时, MA(1)过程的协方差为零。那就是它只有一个周期的记忆。

因此, MA(1)的ACF为

$$ \ rho(k)= \ frac {\ gamma(k)} {\ gamma(0)} = \ begin {cases} 1, ＆\ text {k} = 0 \\\ frac {-\ beta} { 1+ \ beta ^ 2}和＆text {k} \ pm 1 \ end {cases} $$

问题：重做MA(2)的工作

可以看出为什么样本自相关函数在指定移动平均过程的顺序时会很有用：MA(q)过程的自相关函数²(k)有q个非零值(与零显着不同), 并且$ k> q $为零。保持MA不需限制$ \ left \ {\ beta_i \ right \} $。但是, 必须限制$ \ left \ {\ beta_i \ right \} $以确保可逆性。

order$ p $的自动回归：AR($ p $)

令$ \ left \ {Z_t \ right \} $是一个纯随机过程, 均值为零, 方差为$ \ sigma_Z ^ 2 $。如果$$ X_t = \ alpha_1X_ {t-1} + \ alpha_2X_ {t-2} + \ cdots + \ alpha_pX_ {}, 则进程$ \ left \ {X_t \ right \} $将被称为$ p $的自回归过程。 tp} + Z_t $$在阶次$ p $的自回归过程中, 当前观测值$ X_t $(例如今天的收益)是由过去观测值的加权平均值返回到$ p $期间以及随机自变量生成的但使用$ X_t $的过去值, 因此自回归。这些类型的过程由[@ greenwood1920inquiry]引入。上面的AR($ p $)可以用恒定的均值表示

$$ X_t = \ delta + \ alpha_1X_ {t-1} + \ alpha_2X_ {t-2} + \ cdots + \ alpha_pX_ {tp} + Z_t $$, 其中$ \ mu $是一个常数项, 与时间序列和$ \ alpha_1, \ alpha_2, \ ldots, \ alpha_p $可以为正或负。如果$ E [X_t] = E [X_ {t-1}] = \ cdots = E [X_p] = \ mu $, 则AR($ p $)是固定的。从而,

\ begin {align *} E [X_t] = \ mu＆= \ delta + \ alpha_1 \ mu + \ alpha_2 \ mu + \ cdots + \ alpha_p \ mu + 0 \\ \ Rightarrow \ mu＆= \ frac {\ delta} {1- \ alpha_1- \ alpha_2- \ cdots- \ alpha_p} \ end {align *}对于最后一个公式为常量, 我们考虑条件$ \ alpha_1 + \ alpha_2 + \ cdots + \ alpha_p <1 $。

一阶AR流程：AR(1)

考虑以下情况：$ p = 1 $, 然后$$ X_t = \ alpha X_ {t-1} + Z_t $$是一阶自回归AR(1), 也称为马尔可夫过程。使用后移运算符$ BX_t = X_ {t-1} $, 你可以将AR(1)表示为无限MA进程。我们有$$(1-\ alpha B)X_t = Z_t $$因此, \ begin {align *} X_t＆= \ frac {Z_t} {1- \ alpha B} \\＆=(1+ \ alpha B + \ alpha ^ 2B ^ 2 + \ cdots)Z_t \\＆= Z_t + \ alpha Z_ {t-1} + \ alpha ^ 2Z_ {t-2} + \ cdots \\＆= Z_t + \ beta_1 Z_ {t-1} + \ beta_2 Z_ {t-2} + \ cdots \\ \ end {align *}

然后$ E [X_t] = 0 $和$ Var(X_t)= \ sigma ^ 2_Z(1+ \ alpha ^ 2 + \ alpha ^ 4 + \ cdots)$。该级数收敛于条件$ | \ alpha | <1 $。

问题：假设AR(1)进程$ X_t = \ alpha_1X_1 + Z_t $是一个纯随机过程, 均值零且方差$ \ sigma ^ 2_Z $和$ \ alpha $是一个常量, 且对$ \ alpha $具有必要条件, 导出$ X_t $的方差和自协方差函数。

模拟AR(1)

# constant alpha
alpha = 0.5

# purely random process with mean 0 and standard deviation 1.5
Z <- rnorm(100, mean = 0, sd = 1.5)

# seed
X <- rnorm(1)

# the process
for (i in 2:length(Z)) {
  X[i] <- 0.7*X[i-1]+Z[i]
}

# process plotting
ts.plot(X)

问题：表达关于参数值的AR(2)模型的平稳状态。即, 显示以下条件：

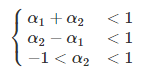
使用R进行时间序列分析1

你也可以将有限阶的AR进程(例如p)表示为无限阶的MA进程。这可以通过连续替换或使用后向移位运算符来完成。

自回归移动平均过程：ARMA($ p, q $)

在模型构建中, 可能有必要在模型中同时混合AR和MA项。这导致混合的自回归–移动平均(ARMA)过程。包含$ p $自回归项和$ q $移动平均项的ARMA流程被称为$(p, q)$阶, 由

$$ X_t = \ alpha_1X_ {t-1} + \ alpha_2X_ {t-2} + \ cdots + \ alpha_pX_ {tp} + Z_t- \ beta_1Z_ {t-1}-\ beta_2Z_ {t-2}-\ cdots- \ beta_qZ_ {tq} $$使用后退运算符B, 该等式可以写为

$$ \ alpha_p(B)X_t = \ beta_q(B)Z_t $$其中$ \ alpha_p(B)$和$ \ beta_q(B)$分别是阶$ p $和$ q $的多项式, 使得

\ begin {align *} \ alpha_p(B)＆= \ left(1- \ alpha_1 B- \ cdots- \ alpha_p B ^ p \ right)\\ \ beta_q(B)＆= \ left(1- \ beta_1 B -\ cdots- \ beta_p B ^ p \ right)\ end {align *}

为了使过程可逆, $ \ beta_q(B)$的根必须位于单位圆之外。为了保持平稳, 我们要求$ \ alpha_p(B)= 0 $的根位于单位圆之外。还假定$ \ alpha_p(B)= 0 $和$ \ beta_q(B)= 0 $没有共同的根。

ARMA(1, 1)流程

此过程的顺序为$(1, 1)$, 并由等式$$ X_t = \ alpha_1X_ {t-1} + Z_t- \ beta_1Z_ {t-1} $$给出

条件为$ | \ alpha_1 | <1 $, 并且用于平稳性可逆证明。当$ \ alpha 0 $时, arma(1, 1)减少为ma(1), 我们将得到ar(1)。可以使用后移p> $$(1- \ alpha_1B)X_t =(1- \ beta_1B)Z_t $$将过程转换为纯自回归表示

我们有

\ begin {align *} \ frac {1- \ alpha_1B} {1- \ beta_1B} X_t＆= Z_t \\ \ pi(B)X_t＆= Z_t \ end {align *}

与

\ begin {align *} \ pi(B)= 1- \ pi_1B- \ pi_2B ^ 2- \ ldots＆= \ frac {1- \ alpha_1B} {1- \ beta_1B} \\(1- \ beta_1B)(1 -\ pi_1B- \ pi_2B ^ 2- \ ldots)＆= 1- \ alpha_1B \\ 1- \ left [(\ pi_1 + \ beta_1)B-(\ pi_2 + \ beta_2)B ^ 2-(\ pi_3 + \ beta_3)B ^ 3 \ right]＆= 1- \ alpha_1B \ end {align *}

通过在等式两边都确定B的系数, 我们得到未知项, 如$$ \ pi_j = \ beta_1 ^ {j-1}(\ alpha_1- \ beta_1), \, \ text {for} \, j \ geq1 $$

ARMA的自相关功能(1, 1)

$ X_t $的期望值由$ E [X_t] = \ alpha_1E [X_ {t-1}] $给出, 在平稳性假设下, 我们有$ E [X_t] = E [X_ {t-1}] = \ mu = 0 $。这对于自动协方差函数的计算很有用, 该函数的获得如下：

  1. $ X_tX_ {t-k} = \ alpha_1X_ {t-k} X_ {t-1} + X_ {t-k} Z_t- \ beta_1X_ {t-k} Z_ {t-1} $
  2. 考虑到双方的期望, 我们得到：\ begin {align *} E \ left [X_tX_ {tk} \ right]＆= E \ left [\ alpha_1X_ {tk} X_ {t-1} \ right] + E \左[X_ {tk} Z_t \ right]-\ beta_1E \左[X_ {tk} Z_ {t-1} \ right] \\ \ gamma(k)＆= \ alpha_1 \ gamma(k-1)+ E \左[X_ {tk} Z_t \ right]-\ beta_1E \左[X_ {tk} Z_ {t-1} \ right] \ end {align *}

对于$ k = 0 $,

\ begin {align *} \ gamma(1)＆= \ alpha_1 \ gamma(0)+ E \ left [X_ {t-1} Z_t \ right]-\ beta_1E \ left [X_ {t-1} Z_ {t -1} \ right] \\＆= \ alpha_1 \ left(\ alpha_1 \ gamma(1)+ \ sigma ^ 2_Z-\ beta_1(\ alpha_1- \ beta_1)\ sigma ^ 2_Z \ right)-\ beta_1 \ sigma ^ 2_Z \\＆= \ alpha ^ 2 \ gamma(1)+(\ alpha_1- \ beta_1)(1- \ alpha_1 \ beta_1)\ sigma ^ 2_Z \\ \ Rightarrow \ gamma(1)＆= \ frac {(\ alpha_1- \ beta_1)(1- \ alpha_1 \ beta_1)\ sigma ^ 2_Z} {1- \ alpha ^ 2} \\ \ Rightarrow \ gamma(0)＆= \ alpha_1 \ frac {(\ alpha_1- \ beta_1)( 1- \ alpha_1 \ beta_1)\ sigma ^ 2_Z} {1- \ alpha ^ 2} + \ sigma ^ 2_Z-\ beta_1(\ alpha_1- \ beta_1)\ sigma ^ 2_Z \\＆= \ frac {\ left(1 + \ beta_1 ^ 2-2 \ alpha_1 \ beta_1 \ right)\ sigma_Z ^ 2} {1- \ alpha ^ 2} \ end {align *}

对于$ k \ geq 2 $,

\ begin {align *} \ gamma(2)＆= \ alpha_1 \ gamma(k-1)\ end {align *}

因此, ARMA(1, 1)的ACF为：

$$ \ rho(k)= \ begin {cases} 1, ＆\ text {for} \, k = 0 \\ \ frac {(\ alpha_1- \ beta_1)(1- \ alpha_1 \ beta_1)} {1+ \ beta_1 ^ 2-2 \ alpha_1 \ beta_1}, ＆\ text {for} \, k = 1 \\ \ alpha_1 \ rho(k-1), ＆\ text {for} \, k \ geq2 \\ \ \ end {cases} $$ ARMA(1, 1)的ACF结合了AR(1)和MA(1)进程的特征。 MA(1)和AR(1)参数都位于$ \ rho(1)$中。在$ \ rho(1)$之外, ARIMA(1, 1)odel的ACF遵循与AR(1)的ACF相同的模式。

问题：查找ARMA(1, 1)进程的部分自相关函数(PACF)。

注意：时间序列过程的特征根据其ACF和PACF给出。时间序列分析中最关键的步骤是, 根据ACF和PACF未知的可用数据, 识别并构建模型。

ARMA(1, 1)过程仿真

# purely random process with mean 0 and standard deviation 1.5
Z <- rnorm(100, mean = 0, sd = 1.5)

# Process
X <- rnorm(1)

for (i in 2:length(Z)) {
  X[i] <- 0.35*X[i-1] + Z[i] + 0.4*Z[i-1]
}

# process plotting
ts.plot(X, main = "ARMA(1, 1) process")

# ACF et PACF
par(mfrow = c(1, 2))
acf(X); pacf(X)

ARIMA($ p, d, q $)流程

自回归综合移动平均模型是由以下方程式定义的时间序列：

SARIMA(p, d, q)(P, D, Q)流程

在本节中, 你将使用实时序列从中拟合最佳模型。为此, 你将使用预测包。函数auto.arima可以从数据中拟合并选择最佳模型, 而预测功能则可以预测前面的h个周期。

# R packages to be used
library(forecast)
library(TSA)

范例1：

# Data from TSA package
data("co2")
data("boardings")

# fitting
fit <- auto.arima(co2)

# Time series plot
plot(fc <- forecast(fit, h = 15))

范例2：

data("boardings")

# fitting
fit2 <- auto.arima(boardings[, "log.price"])

# forecasting
plot(fc2 <- forecast(fit2, h = 15))

参考文献

Greenwood, Major和G Udny Yule。 1920年。”对代表多个事件的频率分布的性质进行的询问, 特别是疾病或反复事故的多次发作的发生。”皇家统计学会杂志83(2)。 JSTOR：255–79。

詹金斯, 总经理。 n.d. “D。 G. Watts(1968)光谱分析及其应用。”旧金山。

总结

在本教程中, 你涵盖了R中时间序列的许多细节。你已经了解了平稳过程是什么, 随机变量的模拟, 随机时间序列的模拟, 随机游走过程等等。此外, 你还介绍了pp阶的自动回归：Ar(pp), SARIMA(p, d, q(P, D, Q)过程, 预测。

如果你想了解有关R中时间序列分析的更多信息, 请参加srcmini的时间序列分析入门课程。

赞(0)
未经允许不得转载：srcmini » 使用R进行时间序列分析
标签：

相关推荐

评论 抢沙发

评论前必须登录！

 

猜你喜欢

热门标签

网站开发 (2587)WordPress开发 (2055)WordPress主题 (1517)Web开发 (692)主题 (528)数据科学 (444)资源合集 (333)合集 (332)教程合集 (317)函数 (287)页面 (267)python开发 (261)百度盘 (245)项目示例 (243)WordPress自定义页面 (233)图像 (219)错误 (213)视频 (195)网站 (190)网红 (189)UX设计 (187)Web安全 (179)模板 (178)Web运维 (177)应用程序 (177)WordPress插件 (176)插件 (171)前端开发 (166)美女 (164)主播 (164)