R中的支持向量机

本文概述

支持向量机算法
非线性数据
R中的支持向量机
总结

在机器学习中, 支持向量机是带有相关学习算法的监督学习模型, 该算法分析用于分类和回归分析的数据。但是, 它们主要用于分类问题。在本教程中, 我们将尝试深入了解SVM的工作原理, 然后使用R来实现它们。我将重点放在发展直觉上, 而不是严格。从本质上讲, 这意味着我们将跳过尽可能多的数学运算, 并对工作原理产生深刻的直觉。

支持向量机算法

线性数据

通过一个简单的示例, 可以最好地理解支持向量机的基础及其工作原理。假设我们有两个标签：红色和蓝色, 而我们的数据有两个功能：x和y。我们想要一个分类器, 给定一对(x, y)坐标, 以红色或蓝色输出。我们将已经标记的训练数据绘制在平面上：

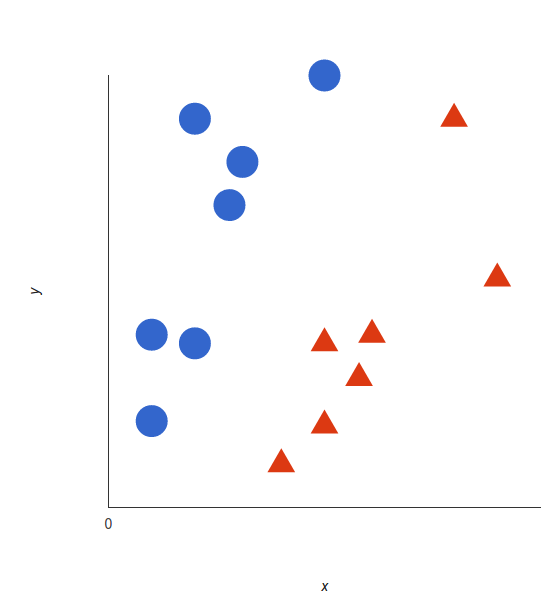
支持向量机获取这些数据点并输出最能分隔标签的超平面(在二维上, 它只是一条线)。这条线是决策边界：落在它一侧的任何东西都将被分类为蓝色, 而落到另一侧的任何东西将被分类为红色。

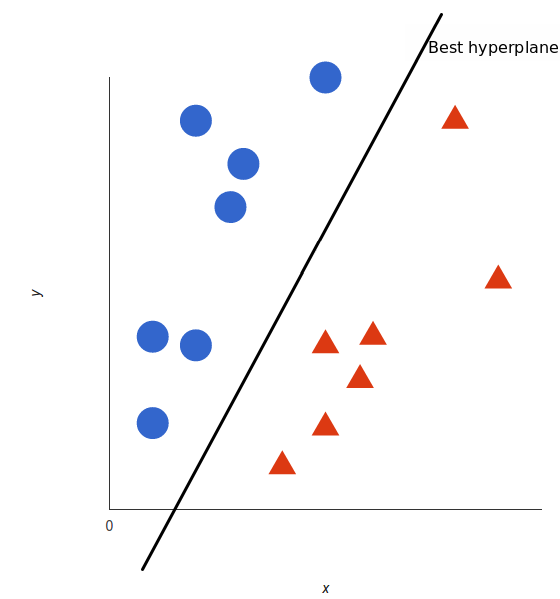
但是, 最好的超平面到底是什么？对于SVM, 它是使两个标签的边距最大化的一种方法。换句话说：超平面(在这种情况下, 请记住是一条线), 其与每个标签的最近元素的距离最大。

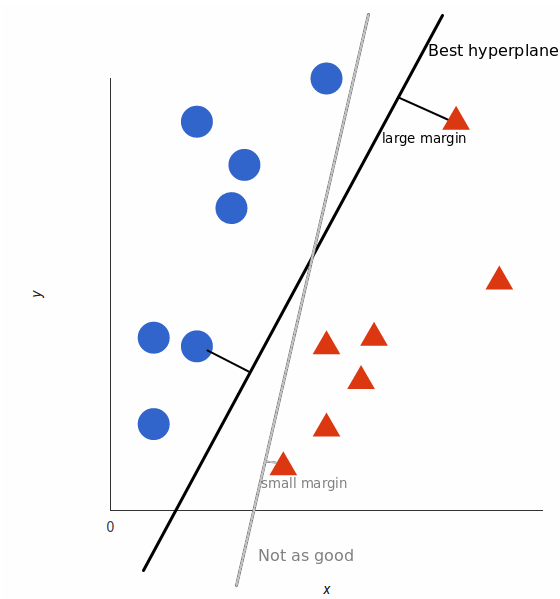
非线性数据

现在上面的示例很简单, 因为很明显, 数据是线性可分离的-我们可以画一条直线来分离红色和蓝色。可悲的是, 通常情况并不那么简单。看一下这种情况：

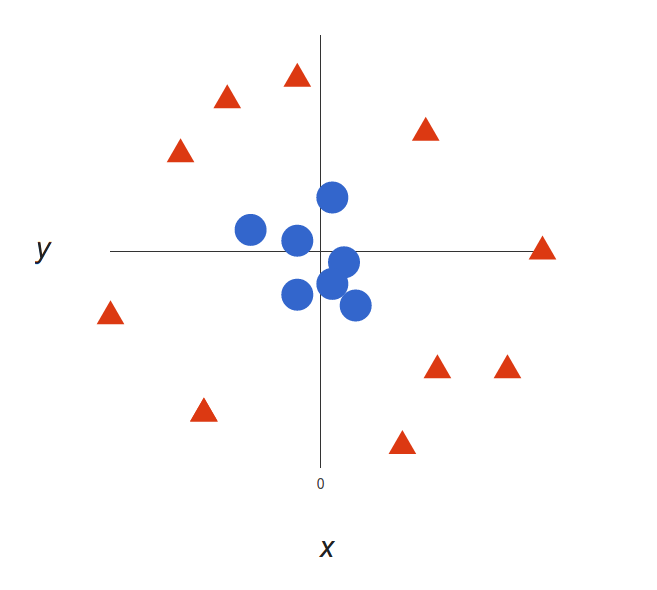
很明显, 没有线性决策边界(将两个标签分开的一条直线)。但是, 这些向量非常清楚地分开了, 看起来好像应该很容易将它们分开。

因此, 我们要做的是：添加第三维。到目前为止, 我们有两个维度：$ x $和$ y $。我们创建了一个新的z维度, 并决定以某种方便的方式对其进行计算：$ z =x²+y²$(你会注意到这是一个圆的方程式)。

这将为我们提供三维空间。占用一部分空间, 它看起来像这样：

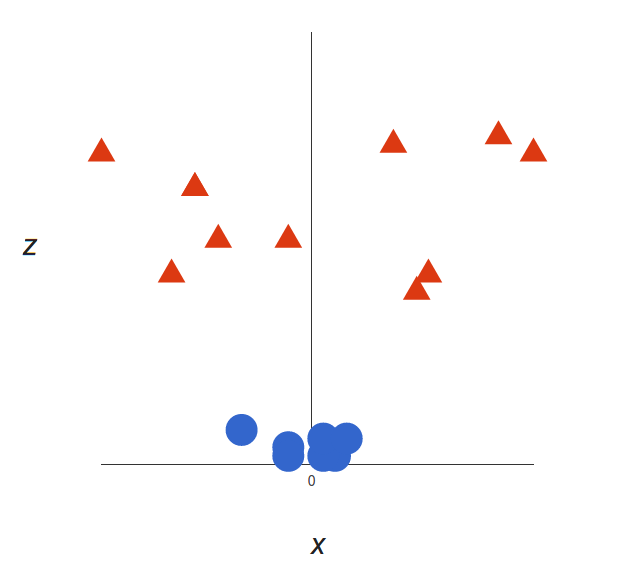
SVM可以做什么？让我们来看看：

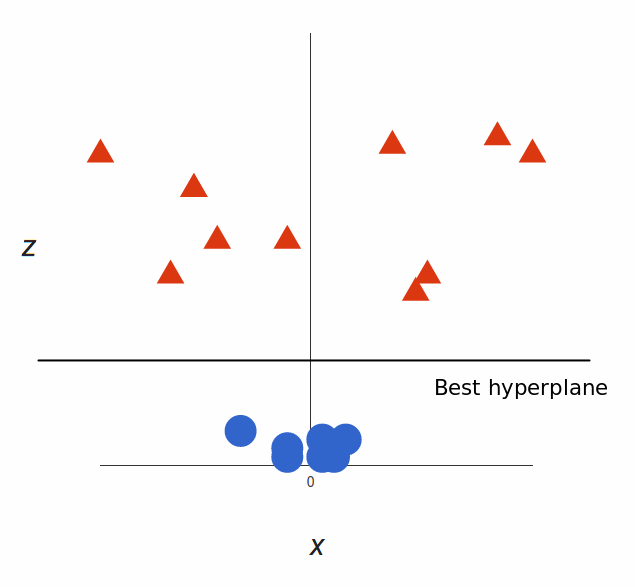
那很棒！请注意, 由于我们现在处于三维, 所以超平面是在某个$ z $处(假设$ z = 1 $)与$ x $轴平行的平面。

剩下的就是将其映射回二维：

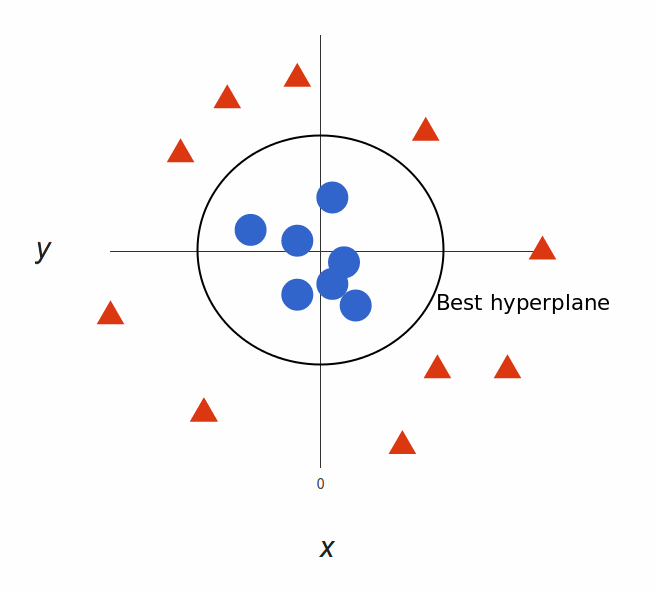
然后我们去！我们的决策边界是半径为1的圆周, 它使用SVM将两个标签分开。

内核技巧

在上面的示例中, 我们找到了一种通过将空间巧妙地映射到更高维度来对非线性数据进行分类的方法。但是, 事实证明, 计算此转换可能会在计算上变得非常昂贵：可能会有很多新维度, 每个维度都可能涉及复杂的计算。为数据集中的每个向量执行此操作可能需要很多工作, 因此, 如果我们能找到更便宜的解决方案, 那就太好了。

这是个窍门：SVM不需要实际的矢量即可发挥其魔力, 它实际上只能通过它们之间的点积来实现。这意味着我们可以回避新尺寸的昂贵计算！这是我们要做的：

想象一下我们想要的新空间：

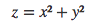
找出该空间中的点积是什么样的：

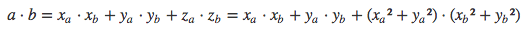
告诉SVM做到这一点, 但要使用新的点积-我们将此称为内核函数。

这被称为内核技巧, 它扩大了特征空间, 以适应类之间的非线性边界。用于分离非线性数据的内核的常见类型是多项式内核, 径向基内核和线性内核(与支持向量分类器相同)。简而言之, 这些内核将数据转换为线性超平面, 从而对数据进行分类。

的优点和缺点

现在让我们看一下SVM的一些优点和缺点：

优点

高维度：SVM是高维度空间中的有效工具, 特别适用于维度可能非常大的文档分类和情感分析。
记忆效率：由于在分配新成员的实际决策过程中仅使用训练点的子集, 因此在进行决策时, 仅需要将这些点存储在内存中(并在此基础上进行计算)。
多功能性：类分隔通常是高度非线性的。应用新内核的能力为决策边界提供了极大的灵活性, 从而提高了分类性能。

缺点

内核参数选择：SVM对内核参数的选择非常敏感。在每个对象的特征数量超过训练数据样本数量的情况下, SVM可能会表现不佳。可以直观地看出, 好像高维特征空间比样本大得多。然后, 在其上不能支持最佳线性超平面的有效支持向量就更少了, 导致在添加新的看不见的样本时分类性能变差。
非概率性：由于分类器通过将对象放置在分类超平面的上方和下方来工作, 因此对于组成员身份没有直接的概率性解释。但是, 一种确定分类”有效性”的潜在指标是新点距决策边界有多远。

线性SVM分类器

首先, 让我们在2维上生成一些数据, 并将它们分开一些。设置随机种子后, 你将生成一个矩阵x, 该矩阵通常在2个变量的2类中分布有20个观测值。然后, 你将创建一个y变量, 该变量将为-1或1, 每个类中有10个。对于y = 1, 可以在每个坐标中将均值从0移到1。最后, 你可以绘制数据并根据其响应对点进行颜色编码。绘图字符19根据响应是1还是-1为你提供漂亮的大可见点, 并用蓝色或红色编码。

set.seed(10111)
x = matrix(rnorm(40), 20, 2)
y = rep(c(-1, 1), c(10, 10))
x[y == 1, ] = x[y == 1, ] + 1
plot(x, col = y + 3, pch = 19)

现在, 你加载包含svm函数的软件包e1071(如果尚未安装, 请记住安装该软件包)。

library(e1071)

现在, 你可以创建数据的数据框, 将y转换为因子变量。之后, 使用y作为响应变量并将其他变量作为预测变量, 在此数据帧上调用svm。该数据帧将把矩阵x解压缩为2列, 分别命名为x1和x2。你告诉SVM内核是线性的, 调入参数cost为10, 并且scale等于false。在此示例中, 你要求它不标准化变量。

dat = data.frame(x, y = as.factor(y))
svmfit = svm(y ~ ., data = dat, kernel = "linear", cost = 10, scale = FALSE)
print(svmfit)

打印svmfit给出其摘要。你可以看到支持向量的数量为6-它们是靠近边界或在边界的错误一侧的点。

如下所示, 有一个SVM的绘图函数显示决策边界。似乎对颜色没有太多控制。它违反了约定, 因为它将x2放在水平轴上, 将x1放在垂直轴上。

plot(svmfit, dat)

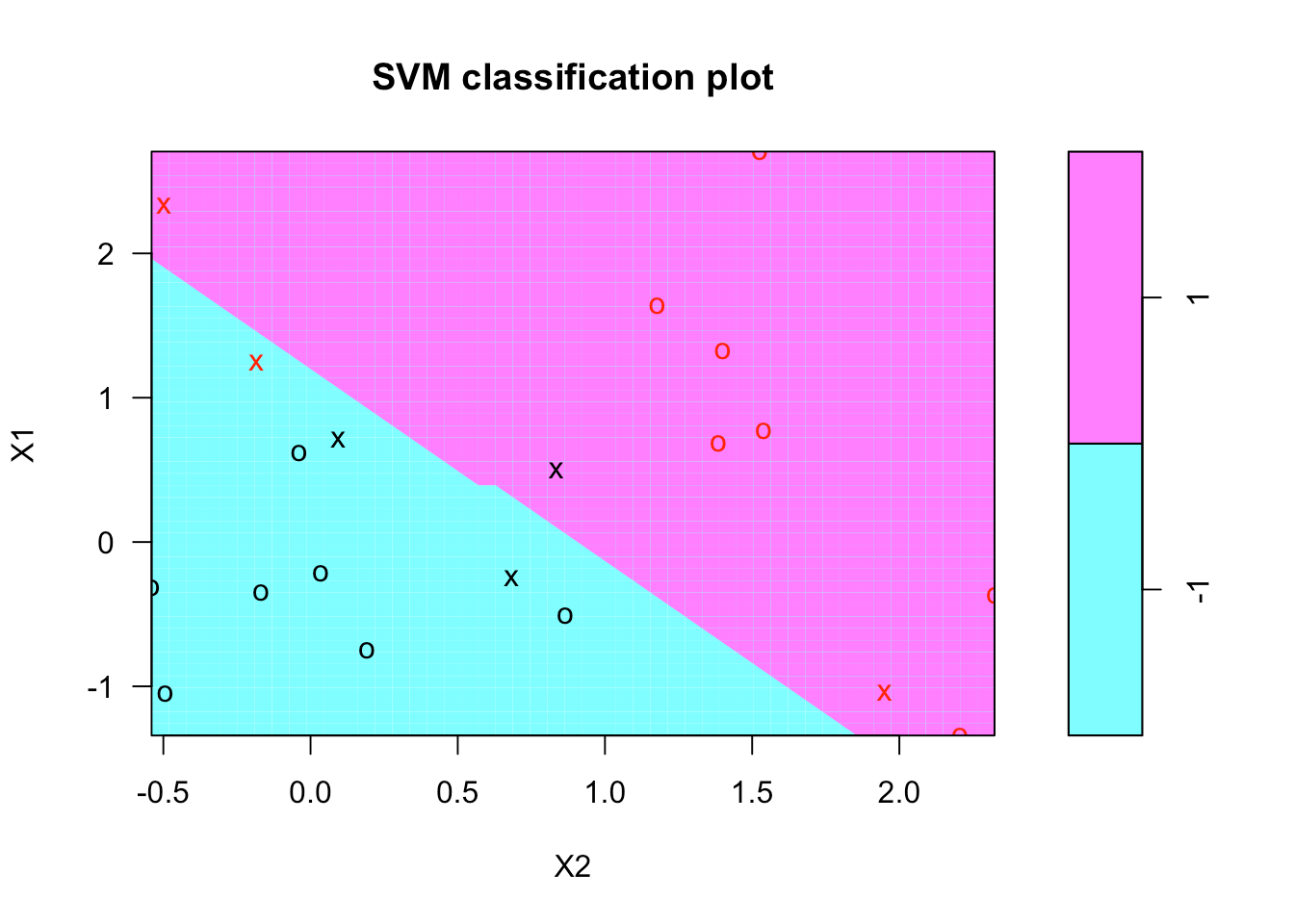
让我们尝试制作自己的情节。首先要做的是为x1和x2创建一个值网格或值网格, 在相当精细的网格上覆盖整个域。为此, 你创建了一个名为make.grid的函数。它包含数据矩阵x以及参数n, 即每个方向上的点数。在这里, 你需要一个75 x 75的网格。

在此函数中, 你可以使用apply函数来获取x中每个变量的范围。然后, 对于x1和x2, 你都可以使用seq函数将最小值从最大值过渡到长度为n的网格。到目前为止, 你拥有x1和x2, 每个坐标在每个坐标上的长度为75个均匀间隔的值。最后, 使用expand.grid函数, 该函数接受x1和x2并生成晶格。

make.grid = function(x, n = 75) {
  grange = apply(x, 2, range)
  x1 = seq(from = grange[1, 1], to = grange[2, 1], length = n)
  x2 = seq(from = grange[1, 2], to = grange[2, 2], length = n)
  expand.grid(X1 = x1, X2 = x2)
}

现在, 你可以在x上应用make.grid函数。让我们看一下从1到10的晶格的前几个值。

xgrid = make.grid(x)
xgrid[1:10, ]

如你所见, 网格首先通过第一个坐标, 而第二个坐标保持不变。

制作完晶格后, 你将在晶格中的每个点进行预测。使用新的数据xgrid, 你可以使用预测并调用响应ygrid。然后根据分类对点进行绘图和颜色编码, 以使决策边界清晰。我们还使用points函数将原始点放在此绘图上。

svmfit有一个称为index的组件, 它可以告诉你哪些支持点。通过再次使用点功能将它们包括在图中。

ygrid = predict(svmfit, xgrid)
plot(xgrid, col = c("red", "blue")[as.numeric(ygrid)], pch = 20, cex = .2)
points(x, col = y + 3, pch = 19)
points(x[svmfit$index, ], pch = 5, cex = 2)

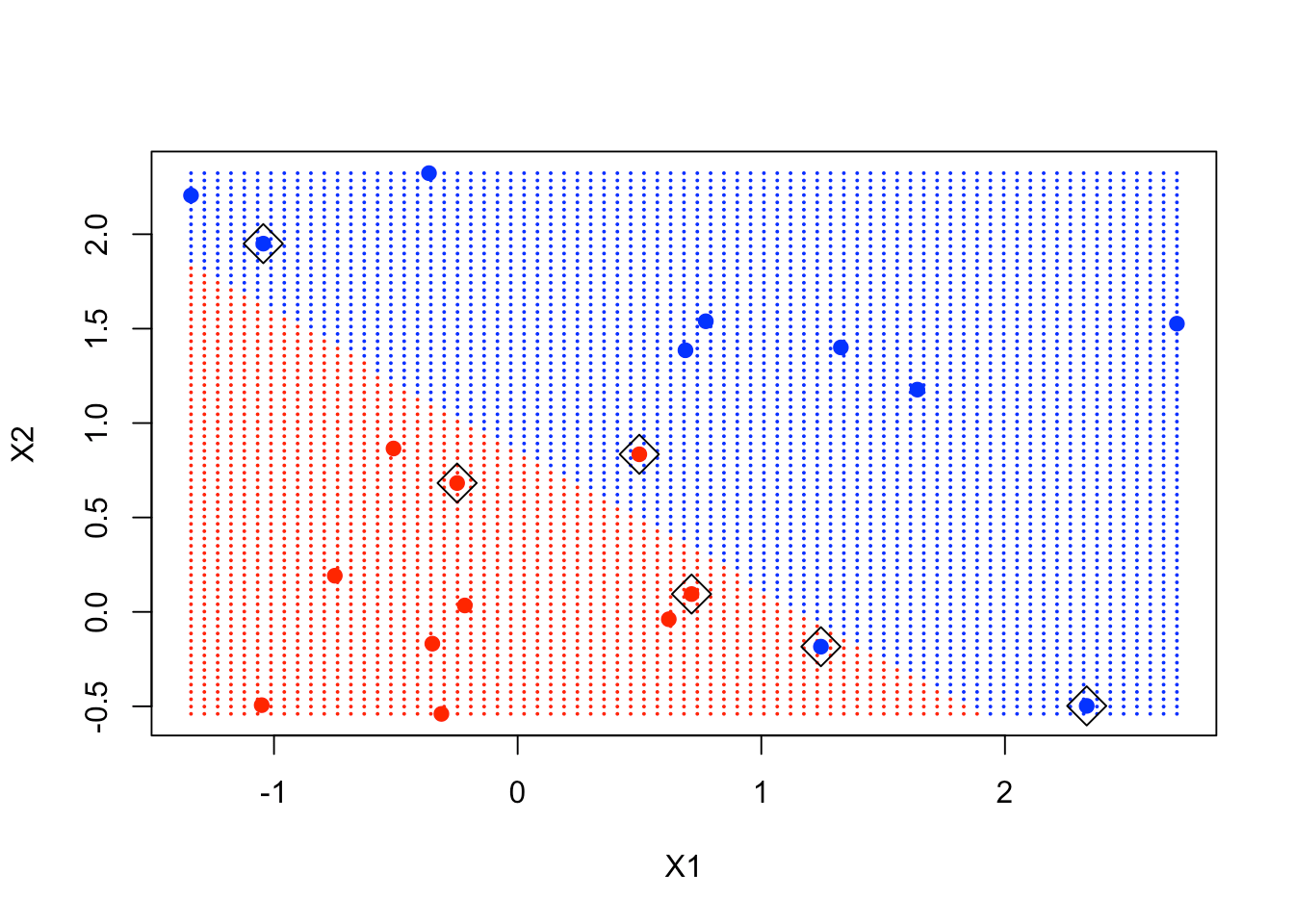
正如你在图中所看到的, 方框中的点靠近决策边界, 并有助于确定该边界。

不幸的是, svm函数不太友好, 因为你必须做一些工作才能取回线性系数。原因可能是这仅对线性核有意义, 并且函数更通用。因此, 让我们使用公式更有效地提取系数。你提取beta和beta0, 这是线性系数。

beta = drop(t(svmfit$coefs)%*%x[svmfit$index, ])
beta0 = svmfit$rho

现在, 你可以重新绘制网格上的点, 然后将其放回去(包括支持向量点)。然后, 你可以使用以下形式的简单方程式, 使用系数来绘制决策边界：

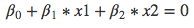
从该方程式中, 你必须找出决策边界的斜率和截距。然后, 你可以将abline函数与这2个参数一起使用。随后的2 abline函数分别代表决策边界的上边界和下边界。

plot(xgrid, col = c("red", "blue")[as.numeric(ygrid)], pch = 20, cex = .2)
points(x, col = y + 3, pch = 19)
points(x[svmfit$index, ], pch = 5, cex = 2)
abline(beta0 / beta[2], -beta[1] / beta[2])
abline((beta0 - 1) / beta[2], -beta[1] / beta[2], lty = 2)
abline((beta0 + 1) / beta[2], -beta[1] / beta[2], lty = 2)

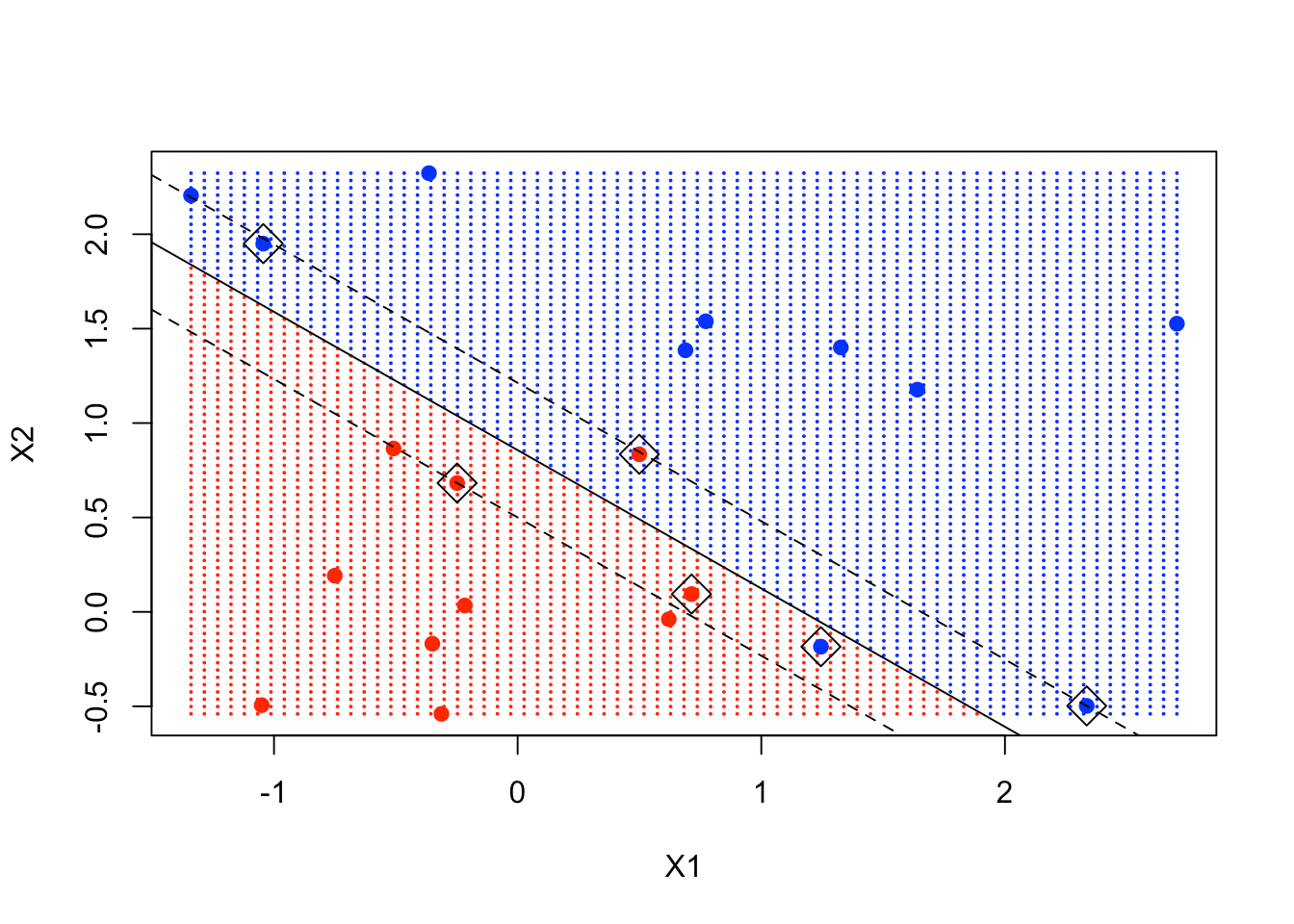
你可以清楚地看到一些支撑点恰好在边缘上, 而有些支撑点在边缘内。

非线性SVM分类器

这就是上一节中的线性SVM。现在, 让我们继续到SVM的非线性版本。你将看一看教科书《统计学学习的元素》中的一个例子, 该书在二维范围内有一个典型的例子, 其中决策边界是非线性的。你将使用内核支持向量机尝试并了解该边界。

首先, 你可以通过直接从该URL(数据所在的网页)下载数据来从教科书中获取该示例的数据。数据被混合并模拟。然后, 你可以检查其列名称。

load(file = "ESL.mixture.rda")
names(ESL.mixture)

目前, 训练数据是x和y。你已经为上一个示例创建了x和y。因此, 让我们摆脱它们, 以便可以附加新数据。

rm(x, y)
attach(ESL.mixture)

数据也是二维的。让我们对它们进行绘图以获得良好外观。

plot(x, col = y + 1)

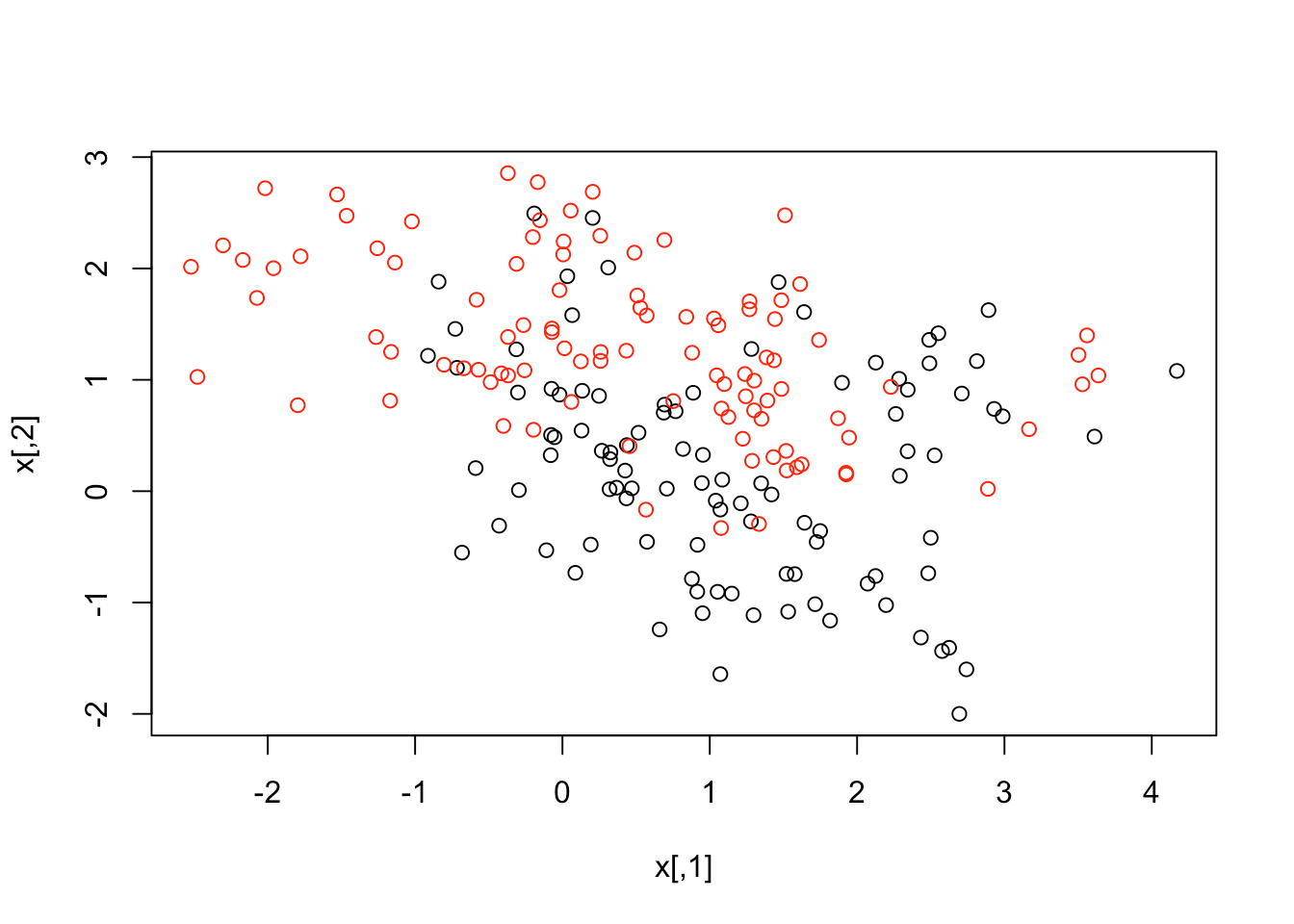
数据似乎有很多重叠, 但是你可以看到它的结构中有一些特殊之处。现在, 让我们创建一个带有响应y的数据框, 并将其变成一个因子。之后, 你可以将SVM与径向内核配合使用, 成本为5。

dat = data.frame(y = factor(y), x)
fit = svm(factor(y) ~ ., data = dat, scale = FALSE, kernel = "radial", cost = 5)

是时候创建一个网格并做出你的预测了。这些数据实际上随网格点一起提供。如果你查看列表中名称的摘要, 则有2个变量px1和px2, 它们是每个变量的值网格。你可以使用expand.grid创建值的网格。然后, 你可以预测网格上每个值的分类。

xgrid = expand.grid(X1 = px1, X2 = px2)
ygrid = predict(fit, xgrid)

最后, 绘制点并根据决策边界为它们着色。你可以看到决策边界是非线性的。你也可以将数据点放在图中, 以查看它们的位置。

plot(xgrid, col = as.numeric(ygrid), pch = 20, cex = .2)
points(x, col = y + 1, pch = 19)

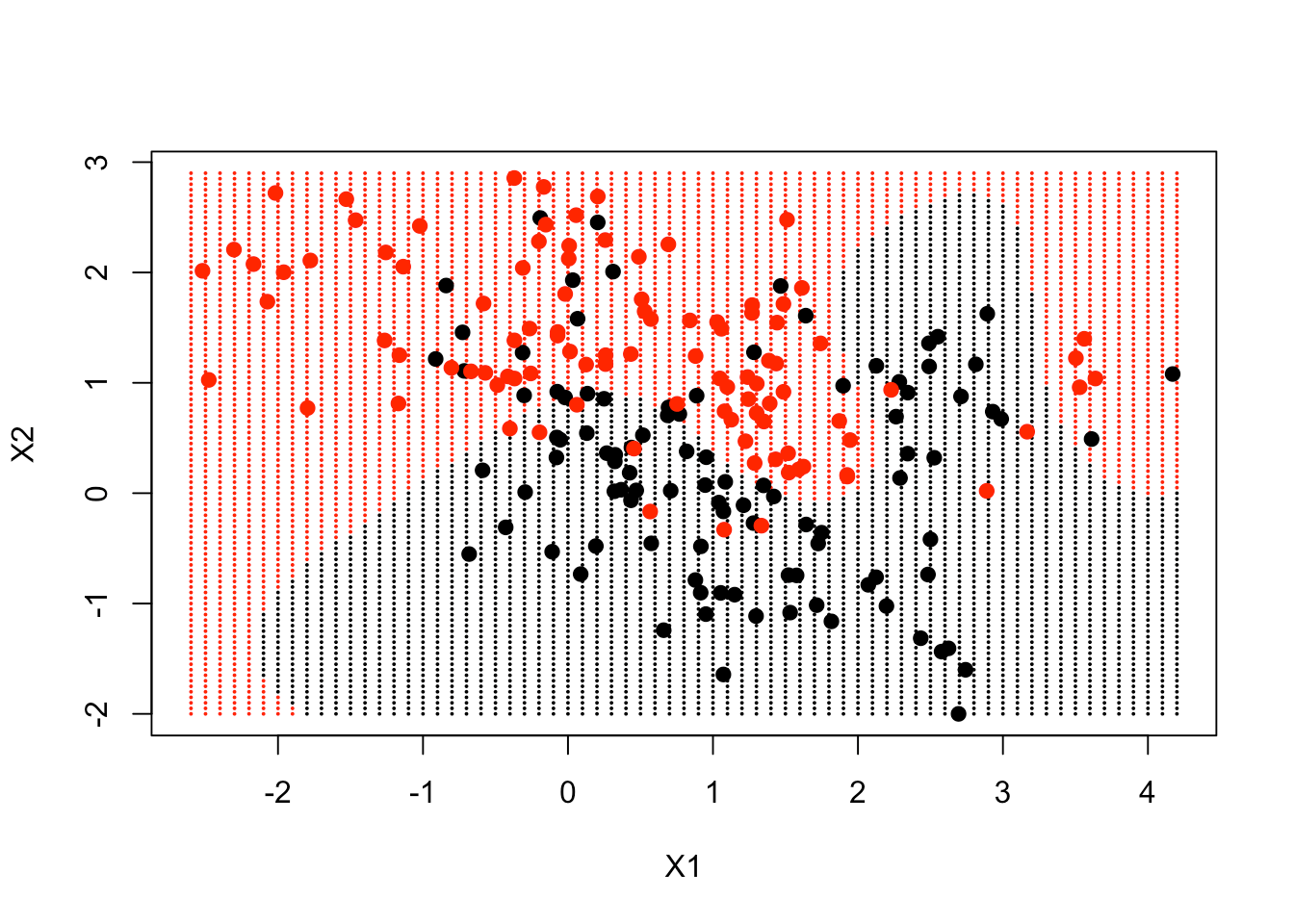
决策边界在很大程度上遵循数据的位置, 但是以非常非线性的方式。

让我们看看是否可以进一步改善此图, 并让预测函数在每个网格点处生成实际函数估计。特别是, 你希望通过使用轮廓函数来绘制一条曲线, 以给出决策边界。在数据帧上, 还有一个称为prob的变量, 它是网格点上这些数据的1类的真实概率。如果绘制其0.5等高线, 将给出贝叶斯决策边界, 这是有史以来最好的。

首先, 你要预测自己在网格上的适合度。你告诉它决策值等于TRUE, 因为你想获得实际的功能, 而不仅仅是分类。它返回实际分类值的属性, 因此你必须提取该属性。然后, 你访问一个称为决策的决策。

接下来, 你可以按照上述相同的步骤创建网格, 进行预测并绘制点。

然后, 该使用轮廓函数了。它需要2个网格序列, 一个函数以及2个参数level和add。你希望函数采用矩阵形式, 其尺寸为px1和px2(分别为69和99)。你将级别设置为0, 并将其添加到绘图中。结果, 你可以看到轮廓跟踪决策边界, 这是在2维中绘制非线性决策边界的便捷方法。

最后, 你包括真相, 它是概率的轮廓。这就是0.5等高线, 它是根据概率确定的决策边界(也称为贝叶斯决策边界)。

func = predict(fit, xgrid, decision.values = TRUE)
func = attributes(func)$decision

xgrid = expand.grid(X1 = px1, X2 = px2)
ygrid = predict(fit, xgrid)
plot(xgrid, col = as.numeric(ygrid), pch = 20, cex = .2)
points(x, col = y + 1, pch = 19)

contour(px1, px2, matrix(func, 69, 99), level = 0, add = TRUE)
contour(px1, px2, matrix(func, 69, 99), level = 0.5, add = TRUE, col = "blue", lwd = 2)

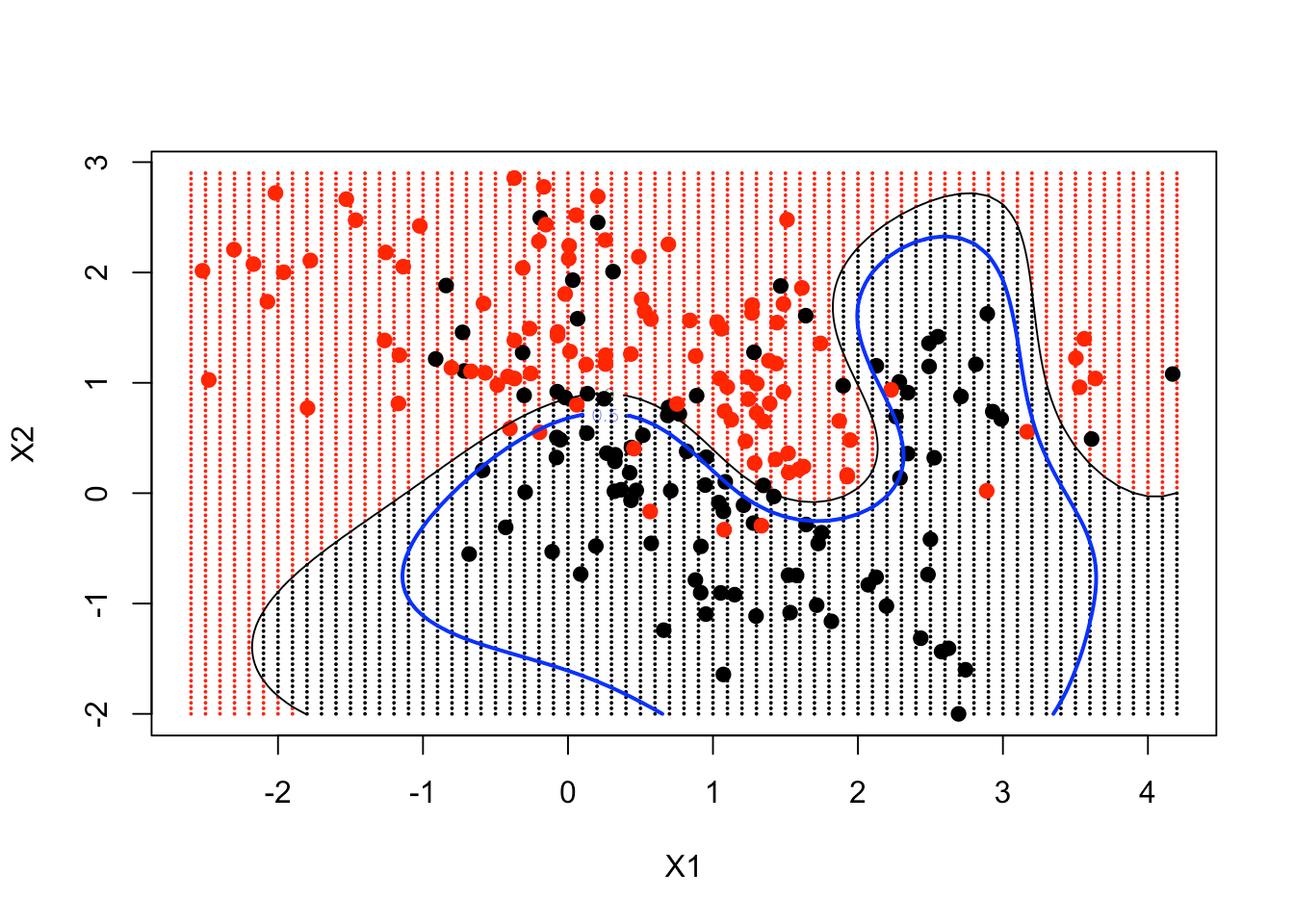
结果, 你可以看到你的非线性SVM已经非常接近贝叶斯决策边界。

总结

综上所述, 支持向量机是有监督分类器的子类, 这些分类器试图将要素空间划分为两个或多个组。他们通过找到一种基于这些类的已知标签来分离此类组的最佳方法来实现这一目标：

在更简单的情况下, 分隔”边界”是线性的, 从而导致在高维空间中被线(或平面)分割的组。
在更复杂的情况下(组之间没有通过线或平面很好地隔开), SVM能够执行非线性分区。这是通过内核功能实现的。
最终, 这使它们成为非常复杂且功能强大的分类器, 但是以通常的代价为代价, 它们可能会过度拟合。

就个人而言, 我认为当特定组明显分开时, SVM对于特定情况是很好的分类器。当你的数据被非线性分离时, 它们也能发挥出色的作用。你可以转换数据以线性分离它, 或者可以让SVM转换数据并线性分离两个类。这是使用SVM的主要原因之一。你不必自己转换非线性数据。 SVM的缺点之一是这些功能的黑匣子性质。使用内核来分离非线性数据使它们难以解释(如果不是不可能的话)。了解它们将为你提供GLM和决策树分类的替代方法。我希望本教程可以使你更全面地了解SVM全景图, 并使你能够更好地了解这些机器。

如果你想了解有关R的更多信息, 请参加srcmini的机器学习工具箱课程。