机器学习涉及预测和分类数据, 为此, 你可以根据数据集采用各种机器学习模型。对机器学习模型进行参数化, 以便可以针对给定问题调整其行为。这些模型可以具有许多参数, 找到参数的最佳组合可以视为搜索问题。但是, 如果你不熟悉应用机器学习, 那么这个称为参数的术语可能对你来说并不熟悉。但是不用担心!你将在本博客的第一篇开始了解它, 并且还将发现机器学习模型的参数和超参数之间的区别是什么。该博客包括以下部分:
- 机器学习模型中的参数和超参数是什么?
- 为什么超参数优化/调整对于提高模型的性能至关重要?
- 优化/调整超参数的两种简单策略
- 使用两种策略的Python简单案例研究
让我们直接进入第一部分!
机器学习模型中的参数是什么?
模型参数是模型内部的配置变量, 其值可以从给定数据中估算出来。
- 模型在进行预测时需要它们。
- 它们的值定义了模型解决问题的技能。
- 它们是从数据估计或学习的。
- 他们通常不是由从业者手动设置的。
- 它们通常被保存为学习模型的一部分。
因此, 你应该从上述观点出发的重点应该是参数对于机器学习算法至关重要。而且, 它们是从历史训练数据中学到的模型的一部分。让我们更深入地研究它。考虑一下一般在编程时使用的功能参数。你可以将参数传递给函数。在这种情况下, 参数是一个函数自变量, 可以具有一个值范围。在机器学习中, 你正在使用的特定模型是该函数, 并且需要参数才能对新数据进行预测。模型是否具有固定或可变数量的参数决定了它可以被称为”参数”还是”非参数”。
模型参数的一些示例包括:
- 人工神经网络中的权重。
- 支持向量机中的支持向量。
- 线性回归或逻辑回归中的系数。
机器学习模型中的超参数是什么?
模型超参数是模型外部的配置, 无法从数据中估计其值。
- 它们通常用于流程中以帮助估计模型参数。
- 它们通常由从业者指定。
- 通常可以使用试探法来设置它们。
- 它们通常针对给定的预测建模问题进行调整。
你不能知道给定问题上模型超参数的最佳值。你可以使用经验法则, 复制在其他问题上使用的值, 或通过反复试验寻找最佳值。当针对特定问题调整机器学习算法时, 从本质上讲, 你是在调整模型的超参数以发现导致最熟练的预测的模型参数。
根据一本非常流行的书, 名为”应用预测建模”, “许多模型具有重要参数, 无法直接从数据中进行估算。例如, 在K近邻分类模型中………这种类型的模型参数称为调整参数, 因为没有可用的分析公式来计算适当的值。”
模型超参数通常被称为模型参数, 可能会使情况变得混乱。克服这种困惑的一个好的经验法则如下:”如果必须手动指定模型参数, 则它可能是模型超参数。 “模型超参数的一些示例包括:
- 训练神经网络的学习率。
- 支持向量机的C和sigma超参数。
- k个近邻中的k个。
在下一节中, 你将发现正确的一组超参数值在机器学习模型中的重要性。
机器学习模型中正确的超参数值集的重要性:
考虑超参数的最佳方式就像可以调整算法以优化性能的设置一样, 就像你可能转动AM收音机的旋钮以获得清晰的信号一样。创建机器学习模型时, 将为你提供有关如何定义模型体系结构的设计选择。通常, 你不立即知道给定模型的最佳模型体系结构, 因此, 你希望能够探索各种可能性。以一种真正的机器学习方式, 理想情况下, 你将要求机器执行此探索并自动选择最佳的模型架构。
你将在案例研究部分中看到有关正确选择超参数值如何影响机器学习模型的性能的信息。在这种情况下, 选择正确的值集通常称为”超参数优化”或”超参数调整”。
优化/调整超参数的两种简单策略:
模型可以具有许多超参数, 并且将参数的最佳组合视为搜索问题。
尽管现在有许多超参数优化/调整算法, 但本文讨论了两种简单的策略:1.网格搜索和2.随机搜索。
网格搜索超参数:
网格搜索是一种超参数调整的方法, 它将针对网格中指定的算法参数的每种组合有条不紊地构建和评估模型。
让我们考虑以下示例:
假设机器学习模型X具有超参数a1, a2和a3。在网格搜索中, 首先要为每个超参数a1, a2和a3定义值的范围。你可以将其视为每个超参数的值数组。现在, 网格搜索技术将使用你首先定义的超参数值(a1, a2和a3)的所有可能组合来构造X的许多版本。超参数值的此范围称为网格。
假设你将网格定义为:
a1 = [0, 1, 2, 3, 4, 5]
a2 = [10, 20, 30, 40, 5, 60]
a3 = [105, 105, 110, 115, 120, 125]
请注意, 为超参数定义的值数组必须合法, 这是因为如果超参数仅采用整数值, 则无法向该数组提供浮点型值。
现在, 网格搜索将开始使用刚刚定义的网格构造X的多个版本的过程。
它将以[0, 10, 105]的组合开始, 并将以[5, 60, 125]结束。它将经历这两者之间的所有中间组合, 这使得网格搜索在计算上非常昂贵。
让我们看一下其他搜索技术随机搜索:
随机搜索超参数:
James Bergstra&Yoshua Bengio提出了随机搜索超参数的想法。你可以在此处检查原始纸张。
随机搜索不同于网格搜索。这样, 你就不再需要为每个超参数提供一组离散的值来进行探索;相反, 你可以为每个超参数提供统计分布, 从中可以随机采样值。
在继续进行之前, 让我们了解分布和抽样的含义:
在统计中, 通过分布, 从本质上讲, 它是指变量值的排列, 表示变量的观察频率或理论发生频率。
另一方面, 抽样是统计中使用的术语。这是从目标人群中选择代表性样本并从该样本中收集数据以了解整个人口的过程。
现在, 让我们再次回到随机搜索的概念。
你将为每个超参数定义一个采样分布。你还可以定义搜索最佳模型时要构建的迭代次数。对于每次迭代, 将通过对定义的分布进行采样来设置模型的超参数值。促使使用随机搜索代替网格搜索的主要理论支持之一是, 在大多数情况下, 超参数并非同等重要。根据原始文件:
“…。对于大多数数据集而言, 只有几个超参数确实很重要, 但是不同的超参数对不同的数据集很重要。这种现象使网格搜索成为为新数据集配置算法的糟糕选择。”
在下图中, 我们正在一个超参数空间中搜索, 在该空间中, 一个超参数对优化模型得分的影响更大-每个轴上显示的分布表示模型的得分。在每种情况下, 我们都在评估九种不同的模型。网格搜索策略公然错过了最佳模型, 并花了很多时间探索不重要的参数。在此网格搜索过程中, 我们隔离了每个超参数, 并在使所有其他超参数保持不变的同时搜索了最佳值。对于正在研究的超参数对所得模型分数影响很小的情况, 这会浪费精力。相反, 随机搜索的探查能力大大提高, 可以集中精力为关键超参数找到最佳值。

资料来源:随机搜索以进行超参数优化
在以下各节中, 你将看到使用Python进行的网格搜索和随机搜索。你还可以决定在效果和效率上哪个更好。
Python案例研究:
超参数调整是呈现结果之前应用机器学习过程的最后一步。
你将使用Pima印度糖尿病数据集。数据集对应于一个分类问题, 鉴于数据集中的8个特征, 你需要根据一个人是否患有糖尿病来做出预测。你可以在此处找到数据集的完整描述。
数据集中共有768个观测值。你的首要任务是加载数据集, 以便继续进行。但是在此之前, 我们需要导入依赖项。
# Dependencies
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
现在已经导入了依赖项, 让我们使用著名的Pandas库将Pima Indians数据集加载到Dataframe对象中。
data = pd.read_csv("diabetes.csv") # Make sure the .csv file and the notebook are residing on the same directory otherwise supply an absolute path of the .csv file
数据集已成功加载到Dataframe对象数据中。现在, 让我们看一下数据。
data.head()
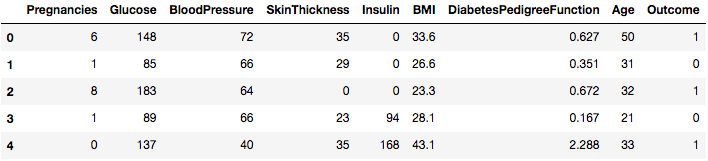
因此, 你可以将8个不同的特征标记为1和0的结果, 其中1代表观察结果患有糖尿病, 0代表观察结果没有糖尿病。已知数据集缺少值。具体而言, 对于某些标记为零值的列, 缺少观测值。我们可以通过这些列的定义来证实这一点, 并且领域知识表明零值对于这些度量无效, 例如, 体重指数或血压为零无效。
(当你尝试建立机器学习模型时, 缺少值会产生很多问题。在这种情况下, 你将使用Logistic回归分类器来预测是否患有糖尿病。现在, Logistic回归无法处理缺少值的问题。 )
(如果要快速了解Logistic回归, 可以在这里参考。)
让我们使用Pandas的describe()实用程序获取有关数据的一些统计信息。
data.describe()
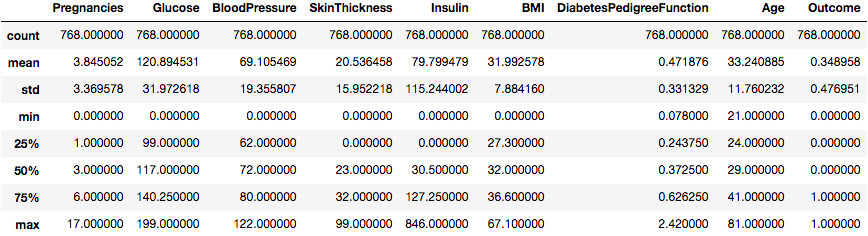
这很有用。
我们可以看到有些列的最小值为零(0)。在某些列上, 零值没有意义, 表示无效或缺失的值。
具体而言, 以下各列具有无效的零最小值:
- 血浆葡萄糖浓度
- 舒张压
- 三头肌皮褶厚度
- 2小时血清胰岛素
- 体重指数
现在, 你需要识别值并将其标记为丢失。让我们通过查看原始数据来确认这一点, 该示例将打印前20行数据。
data.head(20)
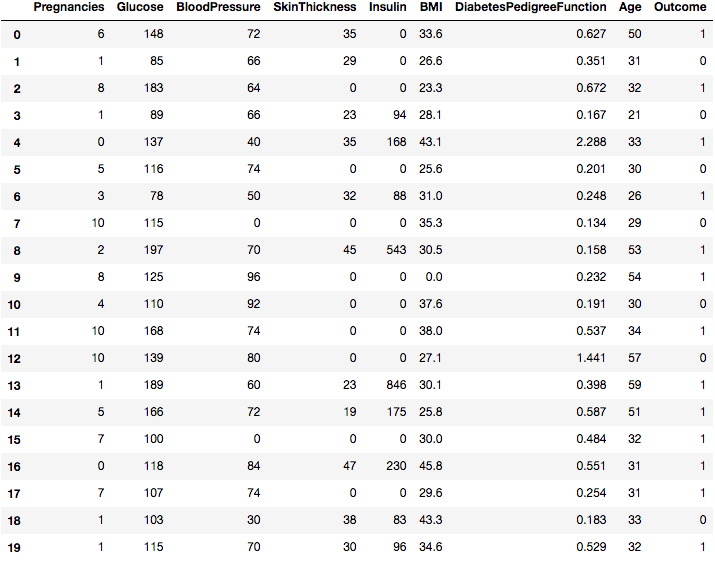
你可以在几列中看到0, 对不对?
你可以在每个这些列中获得缺失值数量的计数。你可以通过将感兴趣的DataFrame子集中具有零值的所有值标记为True来完成此操作。然后, 你可以计算每列中的真值数量。为此, 你将必须重新导入没有列名的数据。
data = pd.read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv", header=None)
print((data[[1, 2, 3, 4, 5]] == 0).sum())
1 5
2 35
3 227
4 374
5 11
dtype: int64
你可以看到第1, 2和5列只有几个零值, 而第3和第4列则显示了更多的值, 几乎占行的一半。尽管第0列有几个缺失值, 但这很自然。第8列表示目标变量, 因此其中的’0’是自然的。
这突出表明, 对于不同的列可能需要不同的”缺失值”策略, 例如, 以确保仍然有足够数量的记录来训练预测模型。
在Python中, 尤其是Pandas, NumPy和Scikit-Learn, 你将缺少的值标记为NaN。
具有NaN值的值将从求和, 计数等操作中忽略。
你可以通过对感兴趣的列的子集使用replace()函数, 使用Pandas DataFrame轻松将值标记为NaN。
标记缺失值之后, 可以使用isull()函数将数据集中的所有NaN值标记为True, 并获取每列的缺失值计数。
# Mark zero values as missing or NaN
data[[1, 2, 3, 4, 5]] = data[[1, 2, 3, 4, 5]].replace(0, np.NaN)
# Count the number of NaN values in each column
print(data.isnull().sum())
0 0
1 5
2 35
3 227
4 374
5 11
6 0
7 0
8 0
dtype: int64
你可以看到列1:5的缺失值数量与上述标识的零值相同。这表明你已正确标记了所标识的缺失值。
这是一个有用的摘要。但是, 你想查看实际数据, 以确认自己没有欺骗自己。
下面是相同的示例, 只不过你打印了前5行数据。
data.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148.0 | 72.0 | 35.0 | NaN | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85.0 | 66.0 | 29.0 | NaN | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183.0 | 64.0 | NaN | NaN | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89.0 | 66.0 | 23.0 | 94.0 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137.0 | 40.0 | 35.0 | 168.0 | 43.1 | 2.288 | 33 | 1 |
从原始数据可以明显看出, 标记缺失值具有预期的效果。现在, 你将估算缺失的值。估算是指使用模型替换缺失值。尽管有几种解决缺失值的解决方案, 但是你将使用均值插补, 这意味着用该特定列的均值替换列中的缺失值。让我们使用Pandas的fillna()实用程序进行此操作。
# Fill missing values with mean column values
data.fillna(data.mean(), inplace=True)
# Count the number of NaN values in each column
print(data.isnull().sum())
0 0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
dtype: int64
干杯!你现在已经处理了价值缺失问题。现在, 让我们使用此数据通过scikit-learn构建Logistic回归模型。
首先, 你将看到带有一些随机超参数值的模型。然后, 你将使用两种不同的策略(网格搜索和随机搜索)构建另外两个Logistic回归模型。
# Split dataset into inputs and outputs
values = data.values
X = values[:, 0:8]
y = values[:, 8]
# Initiate the LR model with random hyperparameters
lr = LogisticRegression(penalty='l1', dual=False, max_iter=110)
你已经使用一些随机超参数值创建了Logistic回归模型。你使用的超参数是:
- 惩罚:用于指定惩罚(正则化)中使用的规范。
- 双重:双重或原始配方。对偶公式化仅使用liblinear求解器实现l2惩罚。当n_samples> n_features时, 首选dual = False。
- max_iter:收敛的最大迭代次数。
在案例研究的后面, 你将优化/调整这些超参数, 以便查看结果的变化。
# Pass data to the LR model
lr.fit(X, y)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=110, multi_class='ovr', n_jobs=1, penalty='l1', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
现在该检查准确性得分了。
lr.score(X, y)
0.7747395833333334
在以上步骤中, 你将LR模型应用于相同的数据并评估了其得分。但是始终需要验证你的机器学习模型的稳定性。你只是无法使模型适合你的训练数据, 并希望它能准确地应用于从未见过的真实数据。你需要某种保证, 以确保你的模型从数据中正确地获得了大多数模式。
好吧, 交叉验证可以帮助你。我将不讨论它的详细信息, 因为它不在本博客的讨论范围之内。但是这篇文章做得很好。
# You will need the following dependencies for applying Cross-validation and evaluating the cross-validated score
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
# Build the k-fold cross-validator
kfold = KFold(n_splits=3, random_state=7)
你提供的n_splits为3, 实际上使它成为3倍交叉验证。你还提供了random_state作为7。这只是为了重现结果。你也可以提供任何整数值。现在, 让我们应用它。
result = cross_val_score(lr, X, y, cv=kfold, scoring='accuracy')
print(result.mean())
0.765625
你会看到分数略有下降。无论如何, 你可以通过超参数调整/优化来做得更好。
让我们构建另一个LR模型, 但是这次将调整它的超参数。你将首先进行此网格搜索。
首先, 导入所需的依赖项。 Scikit-learn为此提供了一个名为GridSearchCV的实用程序。
from sklearn.model_selection import GridSearchCV
让我们定义你在上面使用的超参数的网格值。
dual=[True, False]
max_iter=[100, 110, 120, 130, 140]
param_grid = dict(dual=dual, max_iter=max_iter)
你已经定义了网格。让我们对它们进行网格搜索, 并查看结果和执行时间。
import time
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.752604 using {'dual': False, 'max_iter': 100}
Execution time: 0.3954019546508789 ms
你也可以定义更大的超参数网格, 并应用网格搜索。
dual=[True, False]
max_iter=[100, 110, 120, 130, 140]
C = [1.0, 1.5, 2.0, 2.5]
param_grid = dict(dual=dual, max_iter=max_iter, C=C)
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.763021 using {'C': 2.0, 'dual': False, 'max_iter': 100}
Execution time: 0.793781042098999 ms
你可以看到准确性得分有所提高, 但是执行时间也有足够的增长。网格越大, 执行时间越长。
让我们重新运行所有内容, 但是这次使用随机搜索。 Scikit-learn提供RandomSearchCV来做到这一点。和往常一样, 你将为此导入必要的依赖项。
from sklearn.model_selection import RandomizedSearchCV
random = RandomizedSearchCV(estimator=lr, param_distributions=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
random_result = random.fit(X, y)
# Summarize results
print("Best: %f using %s" % (random_result.best_score_, random_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.763021 using {'max_iter': 100, 'dual': False, 'C': 2.0}
Execution time: 0.28888916969299316 ms
哇!随机搜索产生了相同的准确性, 但时间却少得多。
这就是案例研究的全部内容。现在, 让我们总结一下!
结论和进一步阅读:
在本教程中, 你了解了机器学习模型的参数和超参数以及它们之间的差异。你还知道超参数优化在构建有效的机器学习模型中所起的作用。你借助scikit-learn在Python中构建了一个简单的Logistic回归分类器。
你通过网格搜索和随机搜索对超参数进行了调整, 并观察到哪个参数的性能更好。
此外, 你看到了小的数据预处理步骤(例如处理缺失值), 然后再将数据输入到机器学习模型中。你还介绍了交叉验证。
这需要付出很多, 所有这些在你的数据科学之旅中都同样重要。我将为你提供一些你可以做的进一步阅读。
进一步阅读:
- 超参数优化中的问题
- 使用软计算技术进行超参数优化
- 随机搜索超参数优化
对于那些更高级的人, 我强烈建议阅读本文以有效地优化神经网络的超参数。链接
如果你想了解有关机器学习的更多信息, 请从srcmini学习以下课程。
- 机器学习导论
- 机器学习工具箱
 srcmini
srcmini
评论前必须登录!
注册