本文概述
- 什么是线性回归?
- 在R中创建线性回归。
- 了解系数和残差的概念。
- 如何测试你的线性模型是否合适?
- 检测影响点。
什么是线性回归?
线性回归是一种统计模型, 用于分析响应变量(通常称为y)与一个或多个变量及其相互作用(通常称为x或解释变量)之间的关系。你一直在头脑中建立这种关系, 例如, 当你根据孩子的身高计算孩子的年龄时, 你假设孩子年龄越大, 孩子就会越高。线性回归是最基本的统计模型之一, 其结果几乎可以被每个人解释, 并且它始于19世纪。这正是线性回归如此受欢迎的原因。很简单, 它已经存在了数百年。根据KD Nuggets进行的一项调查, 尽管它不像人工神经网络或随机森林之类的其他算法那么复杂, 但回归是数据科学家在2016年和2017年最常用的算法。甚至预测它仍将是在2118年使用!
在R中创建线性回归。
并非所有问题都可以使用相同的算法解决。在这种情况下, 线性回归假设响应变量和解释变量之间存在线性关系。这意味着你可以在两个(或更多变量)之间划一条线。在前面的示例中, 很明显, 孩子的年龄与其身高之间存在关系。
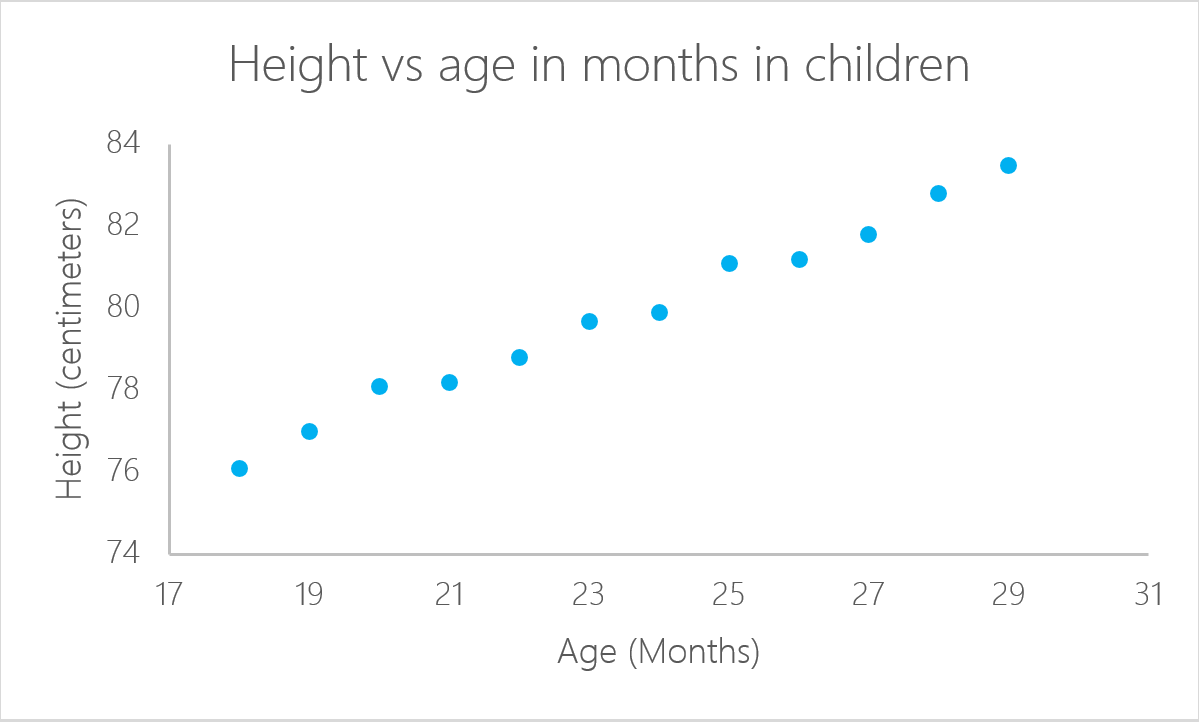
在此特定示例中, 如果你知道孩子的年龄, 则可以计算其身高:
$ \ text {Height} = a + \ text {Age} * b $
在这种情况下, ” a”和” b”分别称为截距和斜率。在相同的示例中, ” a”或截距是你开始测量的值。零个月的新生儿不一定是零厘米。这是拦截的功能。坡度测量的是高度随月龄的变化。通常, 孩子的年龄每增加一个月, 其身高就会增加” b”。
可以使用lm命令在R中计算线性回归。在下一个示例中, 使用此命令根据孩子的年龄计算身高。
首先, 导入库readxl以读取Microsoft Excel文件, 它可以是任何格式, 只要R可以读取它即可。要了解有关将数据导入R的更多信息, 你可以参加此srcmini课程。
可以在此处下载用于本教程的数据。将数据下载到名为ageandheight的对象, 然后在第三行中创建线性回归。 lm命令采用以下格式的变量:
lm([目标变量]〜[预测变量], 数据= [数据源])
使用命令摘要(lmHeight), 你可以查看有关模型性能和系数的详细信息。
library(readxl)
ageandheight <- read_excel("ageandheight.xls", sheet = "Hoja2") #Upload the data
lmHeight = lm(height~age, data = ageandheight) #Create the linear regression
summary(lmHeight) #Review the results
系数。
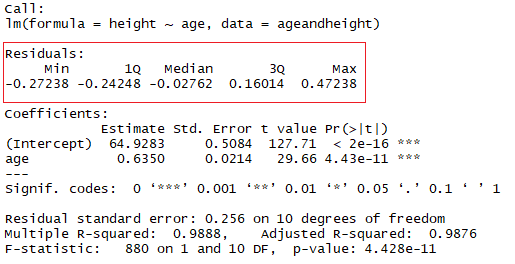
在红色正方形中, 你可以看到年龄的截距值(” a”值)和斜率(” b”值)。这些” a”和” b”值在数据的所有点之间绘制一条线。因此, 在这种情况下, 如果有一个孩子的年龄为20.5个月, 则a为64.92, b为0.635, 该模型(平均)预测其身高(以厘米为单位)约为64.92 +(0.635 * 20.5)= 77.93厘米。
当回归考虑两个或多个预测变量以创建线性回归时, 称为多元线性回归。按照之前简单示例中使用的相同逻辑, 孩子的身高将通过以下方式测量:
身高= a +年龄×b1 +(同胞数}×b2
现在, 你正在查看身高与年龄的关系(以月为单位)以及孩子的兄弟姐妹数。在上图中, 红色矩形表示系数(b1和b2)。你可以通过以下方式解释这些系数:
比较同胞数量相同的孩子时, 孩子每个月的平均预测身高增加0.63 cm。同样, 当比较同龄儿童时, 同胞数量每增加一次, 身高下降-0.01厘米(因为系数为负)。
在R中, 要添加另一个系数, 请为要添加到模型中的每个其他变量添加符号” +”。
lmHeight2 = lm(height~age + no_siblings, data = ageandheight) #Create a linear regression with two variables
summary(lmHeight2) #Review the results
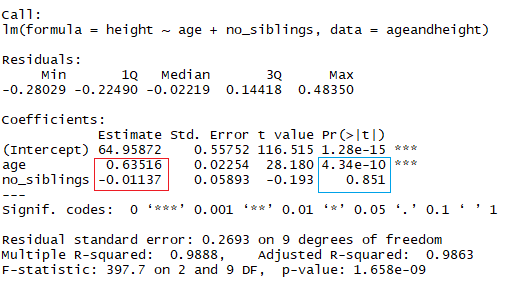
你可能已经注意到, 查看兄弟姐妹的数量是预测孩子身高的一种愚蠢的方法。注意线性模型的另一个方面是系数的p值。在前面的示例中, 蓝色矩形表示年龄和同胞数量的p值。简而言之, p值表示你是否可以拒绝或接受假设。在这种情况下, 假设是预测变量对你的模型没有意义。
- 年龄的p值为4.34 * e-10或0.000000000434。很小的值表示年龄可能是对模型的出色补充。
- 兄弟姐妹数的p值为0.85。换句话说, 此预测变量有85%的可能性对回归没有意义。
测试预测变量是否有意义的一种标准方法是查看p值是否小于0.05。
残差
测试模型拟合质量的一种好方法是查看残差或实际值与预测值之间的差异。上图中的直线表示预测值。从直线到观测数据值的红色垂直线是残差。
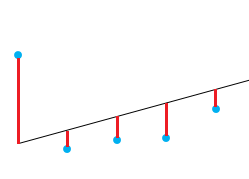
这里的想法是残差之和大约为零或尽可能低。在现实生活中, 大多数情况不会遵循完美的直线, 因此会出现残差。在lm函数的R摘要中, 你可以看到有关模型残差的描述性统计信息, 在同一示例之后, 红色方块显示残差如何近似为零。
如何测试你的线性模型是否合适?
确定系数或R²是用来测试模型质量的一种度量。该度量由回归模型解释的总可变性的比例定义。
$ R ^ 2 = \ frac {\ text {模型的解释变体}} {\ text {模型的总变体}} $
这似乎有些复杂, 但是通常, 对于适合数据的模型, R²接近1。不适合数据的模型的R²接近0。在下面的示例中, 第一个R0.02为0.02。这意味着该模型仅解释了2%的数据可变性。第二个模型的R²为0.99, 该模型可以解释总变异性的99%。**

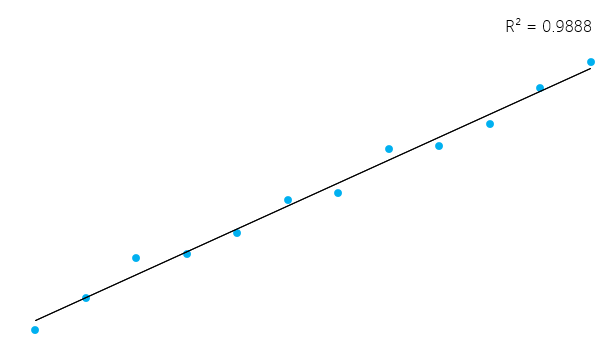
但是, 请务必记住, 有时高R²不一定每次都很好(请参见下面的剩余图), 而低R²不一定总是不好。在现实生活中, 事件并不能始终完美地结合在一起。例如, 你可以在数据中包含相同年龄的较高或较小的孩子。在某些领域, R²为0.5被认为是好的。
与上述相同, 查看线性模型的摘要以了解其R²。
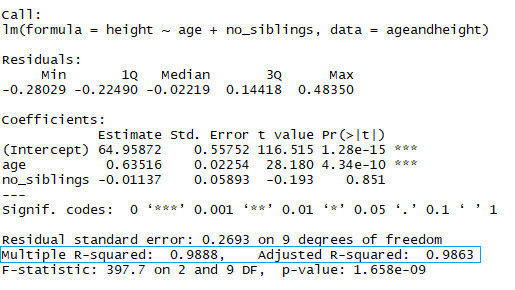
在蓝色矩形中, 请注意, 有两个不同的R², 一个是倍数, 另一个是已调整的。倍数是你先前看到的R²。 R²的一个问题是, 当你向模型中添加更多自变量时, R²不会减小, 即使使这些变量对你的预测没有任何影响(例如, 兄弟姐妹数)。因此, 如果在模型中添加多个变量, 则调整后的R²可能更好看, 因为只有在减少预测的整体误差的情况下, R²才会增加。
别忘了看一下残差!
你的模型中可以有一个相当不错的R², 但是在这里我们不要匆忙得出结论。让我们来看一个例子。你将根据材料的温度预测实验室中材料的压力。
让我们绘制数据(在一个简单的散点图中)并添加你使用线性模型构建的线。在此示例中, 让R首先使用read_excel命令再次读取数据, 以使用数据创建数据框, 然后使用新数据创建线性回归。命令图采用数据框并在其上绘制变量。在这种情况下, 它根据材料的温度绘制压力。然后, 使用命令abline添加通过线性回归生成的线。
pressure <- read_excel("pressure.xlsx") #Upload the data
lmTemp = lm(Pressure~Temperature, data = pressure) #Create the linear regression
plot(pressure, pch = 16, col = "blue") #Plot the results
abline(lmTemp) #Add a regression line

如果你看到新模型的摘要, 则可以看到它的效果很好(请看一下R²和调整后的R²)
summary(lmTemp)
Call:
lm(formula = Pressure ~ Temperature, data = pressure)
Residuals:
Min 1Q Median 3Q Max
-41.85 -34.72 -10.90 24.69 63.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -81.5000 29.1395 -2.797 0.0233 *
Temperature 4.0309 0.4696 8.583 2.62e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 42.66 on 8 degrees of freedom
Multiple R-squared: 0.902, Adjusted R-squared: 0.8898
F-statistic: 73.67 on 1 and 8 DF, p-value: 2.622e-05
理想情况下, 在绘制残差时, 它们应该看起来是随机的。否则意味着可能存在线性模型未考虑的隐藏模式。要绘制残差, 请使用命令plot(lmTemp $ residuals)。
plot(lmTemp$residuals, pch = 16, col = "red")

这可能是一个问题。如果你有更多数据, 则简单的线性模型将无法很好地概括。在上一张图片中, 请注意有一个图案(如残差上的曲线)。这根本不是随机的。
你可以做的是变量的转换。可以对数据执行许多可能的转换, 例如添加二次项$(x ^ 2)$, 三次项$(x ^ 3)$或更复杂的数据, 例如ln(X), ln(X + 1), sqrt(X), 1 / x, Exp(X)。正确转换的选择将带有一些代数函数, 实践, 试验和错误的知识。
让我们尝试一个二次项。为此, 在转换之前添加术语” I”(大写” I”), 例如, 这将是正常的线性回归公式:
lmTemp2 = lm(Pressure~Temperature + I(Temperature^2), data = pressure) #Create a linear regression with a quadratic coefficient
summary(lmTemp2) #Review the results
Call:
lm(formula = Pressure ~ Temperature + I(Temperature^2), data = pressure)
Residuals:
Min 1Q Median 3Q Max
-4.6045 -1.6330 0.5545 1.1795 4.8273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.750000 3.615591 9.335 3.36e-05 ***
Temperature -1.731591 0.151002 -11.467 8.62e-06 ***
I(Temperature^2) 0.052386 0.001338 39.158 1.84e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.074 on 7 degrees of freedom
Multiple R-squared: 0.9996, Adjusted R-squared: 0.9994
F-statistic: 7859 on 2 and 7 DF, p-value: 1.861e-12
请注意, 该模型已大大改善。如果绘制新模型的残差, 它们将如下所示:
plot(lmTemp2$residuals, pch = 16, col = "red")

现在, 你的残留物上看不到任何清晰的图案, 这很好!
检测影响点。
在你的数据中, 你可能具有一些影响点, 这些影响点有时可能会不必要地扭曲你的模型。考虑一下数据输入中的错误, 该值不是写” 2.3″, 而是” 23″。最常见的影响点是离群点, 它们是观察到的响应似乎不遵循其余数据建立的模式的数据点。
你可以通过使用cooks.distance函数查看包含线性模型的对象来检测影响点, 然后绘制这些距离。故意更改一个值, 以查看其在”库克距离”图上的外观。要更改特定值, 你可以使用ageandheight [行号, 列号] = [新值]直接指向它。在这种情况下, 高度将更改为第二个示例的7.7:
ageandheight[2, 2] = 7.7
head(ageandheight)
| 年龄 | 高度 | 无兄弟姐妹 |
|---|---|---|
| 18 | 76.1 | 0 |
| 19 | 7.7 | 2 |
| 20 | 78.1 | 0 |
| 21 | 78.2 | 3 |
| 22 | 78.8 | 4 |
| 23 | 79.7 | 1 |
你再次创建模型, 并查看摘要的拟合度如何, 然后绘制库克距离。为此, 在创建线性回归之后, 请使用命令cooks.distance([linear model], 然后如果需要, 可以使用命令图来绘制这些距离。
lmHeight3 = lm(height~age, data = ageandheight)#Create the linear regression
summary(lmHeight3)#Review the results
plot(cooks.distance(lmHeight3), pch = 16, col = "blue") #Plot the Cooks Distances.
Call:
lm(formula = height ~ age, data = ageandheight)
Residuals:
Min 1Q Median 3Q Max
-53.704 -2.584 3.609 9.503 17.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.905 38.319 0.206 0.841
age 2.816 1.613 1.745 0.112
Residual standard error: 19.29 on 10 degrees of freedom
Multiple R-squared: 0.2335, Adjusted R-squared: 0.1568
F-statistic: 3.046 on 1 and 10 DF, p-value: 0.1115

请注意, 有一点不遵循模式, 可能会影响模型。在这里, 你可以就这一点做出决策, 通常, 有三点原因可以说明这一点如此重要:
- 有人录制错误
- 有人在收集观测值时犯了一个根本错误
- 数据点是完全有效的, 在这种情况下, 模型无法解释行为。
如果大小写为1或2, 则可以删除该点(或更正该点)。如果为3, 则不值得删除有效点;否则, 将其删除。也许你可以尝试使用非线性模型, 而不是像线性回归这样的线性模型。
请注意, 有影响力的点可能是有效点, 请确保在删除数据之前先检查数据及其来源。在统计资料书中经常会出现这样的报价:”有时候, 当我们应该抛出可疑的模型时, 我们会抛出非常好的数据。”
总结
你做到了!线性回归是一个很大的话题, 并且将持续下去。在这里, 我介绍了一些技巧, 这些技巧可以帮助调优并充分利用这种强大而又简单的算法。你还学习了如何理解此简单统计模型的内容以及如何根据需要进行修改。你还可以通过在R控制台上键入”?lm”并查看此处未涵盖的不同参数来探索其他选项。如果你有兴趣研究统计模型, 请继续阅读R中的”统计模型”课程。
 srcmini
srcmini
评论前必须登录!
注册