本文概述
假设你正在玩二十个问题游戏。你的对手秘密选择了一个主题, 你必须弄清楚他/她选择了什么。在每个回合中, 你可能会问是或否的问题, 而你的对手必须如实回答。如何从最少的问题中找出秘密?
很明显, 有些问题比其他的要好。例如, 询问”它会飞吗?”因为你的第一个问题可能是徒劳的, 而问”它还活着吗?”更有用。凭直觉, 你希望每个问题都大大缩小可能的秘密范围, 最终导致你的答案。
这是决策树背后的基本思想。在每一点上, 你都会考虑一组可以对数据集进行分区的问题。你选择提供最佳拆分的问题, 然后再次找到分区的最佳问题。一旦你考虑的所有点都属于同一类, 就停止。这样, 分类的任务就很容易了。你可以简单地抓住一个点, 然后将其夹在树上。这些问题将引导它进入相应的课堂。
由于本教程使用R语言, 因此我强烈建议你根据你的进阶水平来阅读我们的R入门或中级R课程。
在本教程中, 你将学习决策树的不同类型, 优缺点以及如何在R中自己实现这些决策树。
介绍
决策树是一种监督学习算法, 可用于回归和分类问题。它适用于分类和连续输入和输出变量。

让我们在上图中识别出决策树上的重要术语:
- 根节点代表整个种群或样本。它进一步分为两个或多个同构集合。
- 拆分是将一个节点划分为两个或多个子节点的过程。
- 当一个子节点拆分为更多子节点时, 称为决策节点。
- 不分裂的节点称为终端节点或叶子。
- 删除决策节点的子节点时, 此过程称为”修剪”。修剪的相反是拆分。
- 整个树的子部分称为”分支”。
- 分为子节点的节点称为子节点的父节点。子节点称为父节点的子节点。
决策树的类型
回归树
让我们看一下下面的图像, 它有助于可视化由回归树执行的分区的性质。这显示了适合随机数据集的未修剪树和回归树。两种可视化都显示了从树的顶部开始的一系列拆分规则。请注意, 域的每个拆分都与要素轴之一对齐。轴平行分裂的概念直接推广到大于两个的尺寸。对于大小为$ p $的特征空间($ \ mathbb {R} ^ p $的子集), 该空间分为$ M $个区域, $ R_ {m} $, 每个区域为$ p $维”超级块”。

为了构建回归树, 你首先使用递归二进制splititng在训练数据上增长一棵大树, 仅在每个终端节点的观测值少于最小观察次数时才停止。递归二进制拆分是一种贪婪和自上而下的算法, 用于最小化残差平方和(RSS), 该误差度量也用于线性回归设置。在具有M个分区的分区特征空间的情况下, RSS由下式给出:
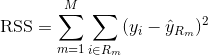
从树的顶部开始, 将其分成2个分支, 创建2个空间的分区。然后, 你可以在树的顶部多次执行此特定拆分, 然后选择功能拆分以最大程度地减少(当前)RSS。
接下来, 将成本复杂度修剪应用于大树, 以获得$ \ alpha $函数的最佳子树序列。这里的基本思想是引入一个附加的调整参数, 用$ \ alpha $表示, 该参数可以平衡树的深度及其与训练数据的拟合优度。
你可以使用K折交叉验证来选择$ \ alpha $。该技术仅涉及将训练观察结果划分为K倍, 以估计子树的测试错误率。你的目标是选择导致最低错误率的那个。
分类树
分类树与回归树非常相似, 区别在于它用于预测定性响应而不是定量响应。
回想一下, 对于回归树, 对观察的预测响应由属于同一终端节点的训练观察的平均响应给出。相反, 对于分类树, 你可以预测每个观察值均属于其所属区域中最常见的训练观察值类别。
在解释分类树的结果时, 你不仅经常对与特定终端节点区域相对应的类别预测感兴趣, 而且还对属于该区域的训练观察结果中的类别比例感兴趣。

增长分类树的任务与增长回归树的任务非常相似。就像在回归设置中一样, 你使用递归二进制拆分来增长分类树。但是, 在分类设置中, 残差平方和不能用作进行二进制分割的标准。而是, 你可以使用以下三种方法之一:
- 分类错误率:你可以将”命中率”定义为特定区域中不属于特定区域的训练观测值的百分比, 而不是像在回归设置中那样看到数值响应与平均值有多远发生最广泛的一类。误差由下式给出:
E = 1-argmaxc($ \ hat {\ pi} _ {mc} $)
其中$ \ hat {\ pi} _ {mc} $代表区域Rm中属于类c的训练数据的一部分。
- 基尼系数(Gini Index):基尼系数(Gini Index)是一种替代误差度量标准, 旨在显示区域的”纯”程度。在这种情况下, “纯度”是指特定区域中有多少训练数据属于单个类别。如果区域Rm包含的数据大部分来自单个c类, 那么Gini索引值将很小:
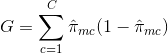
- 交叉熵:与基尼系数相似的第三种替代方法被称为交叉熵或偏差:
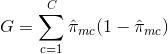
如果$ \ hat {\ pi} _ {mc} $都接近0或接近1, 则交叉熵的值将接近零。因此, 像基尼系数一样, 交叉熵的值将为a。如果第m个节点是纯节点, 则为小值。实际上, 事实证明, 基尼系数和交叉熵在数值上非常相似。
建立分类树时, 通常使用基尼系数或交叉熵来评估特定拆分的质量, 因为它们对节点纯度的敏感性比分类错误率更敏感。修剪树时可以使用这三种方法中的任何一种, 但是如果以最终修剪树的预测精度为目标, 则分类错误率是可取的。
决策树的优缺点
使用决策树的主要优点是直观上很容易解释。与其他回归和分类方法相比, 它们紧密反映了人类的决策。它们可以以图形方式显示, 并且可以轻松处理定性预测变量, 而无需创建虚拟变量。
但是, 决策树通常不具有与其他方法相同的预测准确性, 因为它们不够鲁棒。数据的微小变化会导致最终估计树的较大变化。
通过聚集许多决策树, 使用装袋, 随机森林和增强等方法, 可以大大提高决策树的预测性能。
基于树的方法
装袋
上面讨论的决策树具有很大的方差, 这意味着如果你将训练数据随机分为两部分, 并将决策树适合两个半部分, 则得到的结果可能会大不相同。相比之下, 如果将方差重复应用于不同的数据集, 则方差小的程序将产生相似的结果。
套袋或自举聚合是一种技术, 可用于通过组合对同一数据集的不同子样本建模的多个分类器的结果来减少预测的方差。这是装袋的等式:
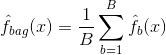
在其中你生成$ B $个不同的自举训练数据集。然后, 你在$ bth $自举训练集中训练你的方法, 以获得$ \ hat {f} _ {b}(x)$, 最后对预测取平均。
下图显示了装袋的3个不同步骤:
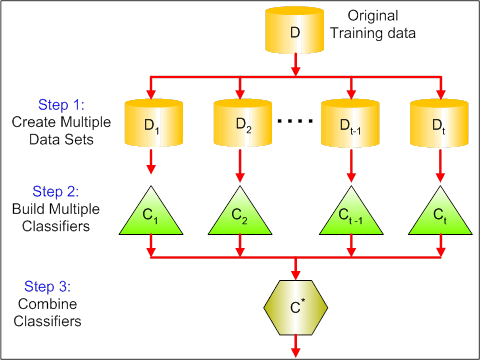
- 步骤1:在这里, 你将原始数据替换为新数据。新数据通常只有原始数据的列和行的一部分, 然后可以在装袋模型中用作超参数。
- 步骤2:你在每个数据集上构建分类器。通常, 你可以使用相同的分类器进行模型和预测。
- 步骤3:最后, 根据问题, 使用平均值组合所有分类器的预测。通常, 这些组合值比单个模型更健壮。
尽管装袋可以改善许多回归和分类方法的预测, 但对于决策树特别有用。要将装袋应用于回归/分类树, 你只需使用$ B $自举训练集构建$ B $回归/分类树, 然后对所得预测取平均值。这些树木长得很深, 没有修剪过。因此, 每个单独的树具有较高的方差, 但具有较低的偏差。对这些$ B $树进行平均可减少方差。
广义上讲, 通过套袋将数百甚至数千棵树合并为一个程序, 事实证明装袋可以显着提高准确性。
随机森林
随机森林是一种通用的机器学习方法, 能够执行回归和分类任务。它还采用降维方法, 处理缺失值, 离群值和数据探索的其他必要步骤, 并且表现出色。
通过对树进行解相关的小调整, Random Forests对袋装树进行了改进。与装袋一样, 你可以在自举训练样本上构建许多决策树。但是, 在构建这些决策树时, 每次考虑在树中进行拆分时, 都会从完整的$ p $个预测变量集中选择m个预测变量的随机样本作为拆分候选。拆分只允许使用那些$ m $预测变量中的一个。这是随机森林和套袋之间的主要区别。因为在装袋中, 预测变量$ m = p $的选择。

为了种植随机森林, 你应该:
- 首先, 假设训练集中的案例数为K。然后, 从这K个案例中随机抽取一个样本, 然后将该样本用作训练树的训练集。
- 如果有$ p $个输入变量, 请指定数字$ m <p $, 以便在每个节点上可以从$ p $中选择$ m $个随机变量。这些$ m $的最佳拆分用于拆分节点。
- 随后将每棵树最大程度地生长, 并且不需要修剪。
- 最后, 汇总目标树的预测以预测新数据。
当大部分数据丢失时, Random Forests在估计丢失数据和保持准确性方面非常有效。它还可以平衡类不平衡的数据集中的错误。最重要的是, 它可以处理大规模的海量数据集。但是, 使用随机森林的一个缺点是, 你可能容易过度拟合嘈杂的数据集, 尤其是在进行回归的情况下。
助推
增强是另一种改善决策树产生的预测的方法。像套袋和随机森林一样, 它是一种通用方法, 可以应用于许多用于回归或分类的统计学习方法。回想一下, 套袋涉及使用引导程序创建原始训练数据集的多个副本, 将单独的决策树拟合到每个副本, 然后组合所有树以创建单个预测模型。值得注意的是, 每棵树都建立在自举数据集中, 与其他树无关。
除了树木是按顺序生长之外, 增强的工作方式也相似:每棵树都是使用先前生长的树木中的信息进行生长的。升压不涉及自举采样;相反, 每棵树都适合原始数据集的修改版本。
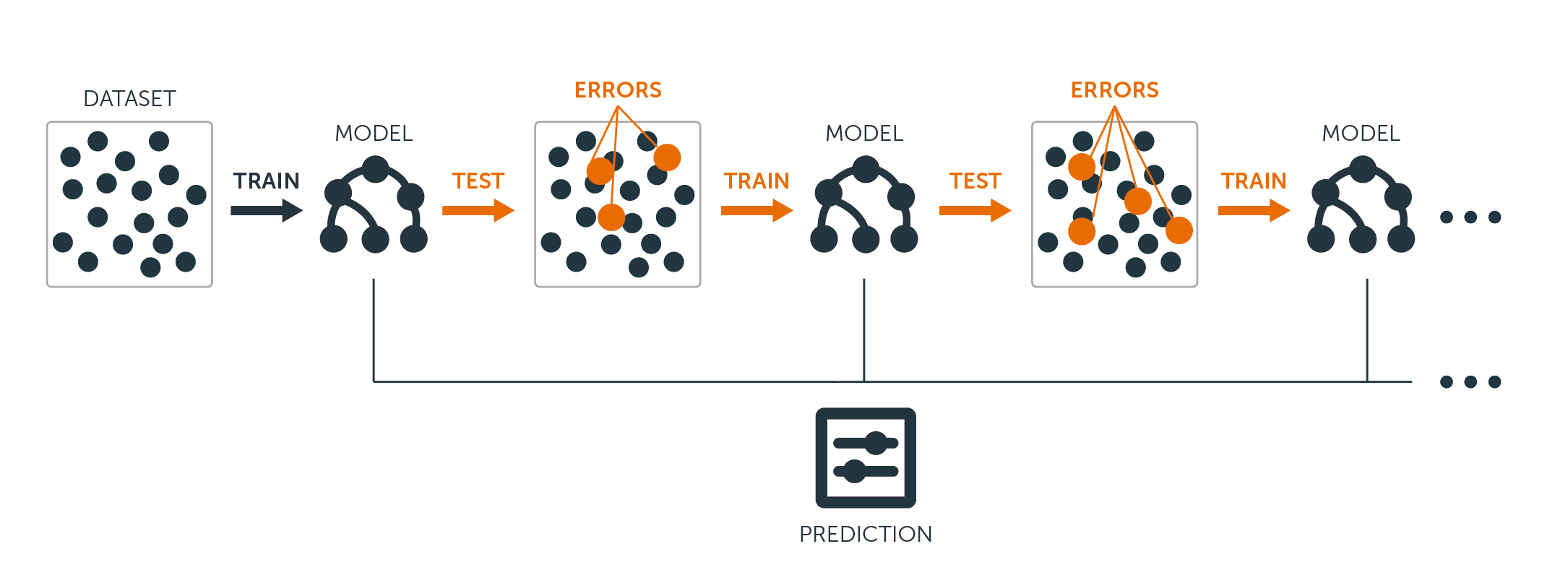
对于回归树和分类树, 增强工作如下:
- 与将单个大型决策树拟合到数据不同, 后者相当于很难对数据进行拟合并可能过度拟合, 而提升方法则学习起来很慢。
- 给定当前模型, 你可以将决策树拟合模型的残差。也就是说, 你使用当前残差而不是结果$ Y $作为响应来拟合树。
- 然后, 你将此新决策树添加到拟合函数中, 以更新残差。这些树中的每一个都可能很小, 只有几个终端节点, 由算法中的参数$ d $确定。通过将小树拟合到残差, 可以在效果不佳的地方慢慢改善$ \ hat {f} $。
- 收缩参数$ \ nu $进一步降低了处理速度, 从而允许更多不同形状的树攻击残差。
当你拥有大量数据并且期望决策树非常复杂时, 提升非常有用。 Boosting已用于解决许多具有挑战性的分类和回归问题, 包括风险分析, 情绪分析, 预测性广告, 价格建模, 销售估算和患者诊断等。
R中的决策树
分类树
对于这一部分, 你将使用R中的树包来使用Carseats数据集。请记住, 你需要首先在R Studio环境中安装ISLR和树包。让我们首先从ISLR包中加载Carseats数据帧。
library(ISLR)
data(package="ISLR")
carseats<-Carseats
让我们也加载树包。
require(tree)
Carseats数据集是一个包含以下11个变量的400个观测值的数据框:
- 销售:单位销售成千上万
- CompPrice:竞争对手在每个位置收取的价格
- 收入:社区收入水平(以千美元计)
- 广告:每个位置的本地广告预算(以1000美元计)
- 人口:地区流行人口
- 价格:每个站点的汽车座椅价格
- ShelveLoc:不良, 良好或中度表示货架位置的质量
- 年龄:人口的年龄水平
- 教育程度:所在位置的教育水平
- 城市:是/否
- 美国:是/否
names(carseats)
让我们看一下汽车销售的直方图:
hist(carseats$Sales)
请注意, Sales是一个定量变量。你想使用带有二进制响应的树来演示它。为此, 请将Sales转换为二进制变量, 该变量将称为High。如果销售额小于8, 则不会很高。否则, 它将很高。然后, 你可以将该新变量High放回数据框中。
High = ifelse(carseats$Sales<=8, "No", "Yes")
carseats = data.frame(carseats, High)
现在, 让我们使用决策树填充模型。当然, 这里没有Sales变量, 因为你的响应变量High是从Sales创建的。因此, 让我们排除它并拟合树。
tree.carseats = tree(High~.-Sales, data=carseats)
我们来看一下分类树的摘要:
summary(tree.carseats)
你可以看到涉及的变量, 终端节点的数量, 剩余平均偏差以及错误分类错误率。为了使其更直观, 我们还绘制树, 然后使用方便的文本功能对其进行注释:
plot(tree.carseats)
text(tree.carseats, pretty = 0)
变量太多了, 看树变得非常复杂。至少, 你可以看到在每个终端节点上, 它们分别标记为”是”或”否”。在每个拆分节点上, 均会显示变量和拆分选项的值(例如, Price <92.5或Advertising <13.5) 。
有关树的详细摘要, 只需打印它即可。如果你想从树中提取细节用于其他目的, 这将很方便:
tree.carseats
现在是时候修剪树了。让我们通过将careats数据帧分为250个训练样本和150个测试样本来创建训练集和测试。首先, 设置种子以使结果可重复。然后, 你随机抽取样本的ID(索引)编号。特别是在这里, 你从设置的1到n行汽车座椅行数(即400)中进行采样。你想要的样本大小为250(默认情况下, 样本用途无需更换)。
set.seed(101)
train=sample(1:nrow(carseats), 250)
因此, 现在你获得了该火车索引, 该索引索引了400个观测值中的250个。你可以使用相同的公式用树来拟合模型, 只是告诉树使用子集等于训练。然后让我们作图:
tree.carseats = tree(High~.-Sales, carseats, subset=train)
plot(tree.carseats)
text(tree.carseats, pretty=0)
由于数据集略有不同, 该图看起来有些不同。然而, 树的复杂度看起来大致相同。
现在, 你将使用这棵树, 并使用树的预测方法在测试集上对其进行预测。在这里, 你将要实际预测类标签。
tree.pred = predict(tree.carseats, carseats[-train, ], type="class")
然后, 你可以使用错误分类表来评估错误。
with(carseats[-train, ], table(tree.pred, High))
对角线是正确的分类, 而对角线是错误的分类。你只想记录正确的内容。为此, 你可以将2个对角线的总和除以总数(150个测试观察值)。
(72 + 43) / 150
好的, 此树的错误为0.76。
当种植一棵大的浓密树时, 它可能会有太多差异。因此, 让我们使用交叉验证对树进行最佳修剪。使用cv.tree, 你将使用错误分类错误作为进行修剪的基础。
cv.carseats = cv.tree(tree.carseats, FUN = prune.misclass)
cv.carseats
打印结果将显示交叉验证路径的详细信息。你可以看到修剪后的树的大小, 修剪过程中的偏差以及过程中使用的成本复杂性参数。
让我们来画一下:
plot(cv.carseats)
查看该图, 你会看到一个向下的螺旋部分, 这是由于250个交叉验证点上的分类错误所致。因此, 让我们在向下的步骤(12)中选择一个值。然后, 我们将树修剪成12的大小以识别该树。最后, 让我们绘制并注释该树以查看结果。
prune.carseats = prune.misclass(tree.carseats, best = 12)
plot(prune.carseats)
text(prune.carseats, pretty=0)
它比以前的树浅一些, 你实际上可以阅读标签。让我们再次在测试数据集上对其进行评估。
tree.pred = predict(prune.carseats, carseats[-train, ], type="class")
with(carseats[-train, ], table(tree.pred, High))
(74 + 39) / 150
似乎正确的分类有些下降。它的工作原理与原始树相同, 因此修剪不会对分类错误产生太大的影响, 并提供了更简单的树。
通常情况下, 树木不会给出很好的预测误差, 因此让我们继续看一下随机森林和助推器, 就预测和错误分类而言, 它们往往胜过树木。
随机森林
对于这一部分, 你将使用波士顿的房屋数据来探索随机森林并进行助推。数据集位于MASS包中。根据1970年的人口普查, 该报告提供了波士顿506个郊区中每个郊区的房屋价值和其他统计数据。
library(MASS)
data(package="MASS")
boston<-Boston
dim(boston)
names(boston)
让我们也加载randomForest包。
require(randomForest)
为了准备随机森林的数据, 让我们设置种子并创建一个包含300个观测值的样本训练集。
set.seed(101)
train = sample(1:nrow(boston), 300)
在该数据集中, 波士顿有506个郊区。对于每个附属项, 你都有变量, 例如人均犯罪率, 行业类型, 每个住宅的平均房间数量, 房屋的平均年龄比例等。让我们使用medv-这些附属项中每个拥有者的房屋中位数, 作为响应变量。
让我们拟合一个随机森林, 看看它的性能如何。如前所述, 你使用响应medv, 房屋中位数($ 1K美元)和训练样本集。
rf.boston = randomForest(medv~., data = boston, subset = train)
rf.boston
打印出随机森林可得到其摘要:树木数量(已种植500棵), 均方差残差(MSR)和方差百分比得到了说明。解释的MSR和%方差是基于实际价格估算的, 这是随机森林中非常聪明的设备, 用于获取真实的误差估算。
随机森林中唯一的调整参数是称为mtry的参数, 该参数是进行拆分时在每个树的每个拆分处选择的变量数。就像这里看到的那样, mtry是波士顿房屋数据中13个探索变量(不包括medv)中的4个-意味着每次树分割节点时, 都会随机选择4个变量, 然后将分割限制为1这四个变量中的一个这就是randomForests使树木不相关的方式。
你将要适合一系列随机森林。有13个变量, 因此我们将mtry的范围设置为1到13:
- 为了记录错误, 你设置了两个变量oob.err和test.err。
- 在从1到13的mtry循环中, 首先将TrainFor数据集上具有mtry值的randomForest拟合, 将树数限制为350。
- 然后提取对象上的均方误差(袋外误差)。
- 然后, 使用拟合(randomForest的拟合)对测试数据集(波士顿[-train])进行预测。
- 最后, 你计算出测试误差:均方误差, 等于均值((medv-pred)^ 2)。
oob.err = double(13)
test.err = double(13)
for(mtry in 1:13){
fit = randomForest(medv~., data = boston, subset=train, mtry=mtry, ntree = 350)
oob.err[mtry] = fit$mse[350]
pred = predict(fit, boston[-train, ])
test.err[mtry] = with(boston[-train, ], mean( (medv-pred)^2 ))
}
基本上你只种了4550棵树(350棵13倍)。现在让我们使用matplot命令进行绘图。将测试错误和袋外错误绑定在一起以创建2列矩阵。矩阵中还有其他一些参数, 包括绘图字符值(pch = 23表示填充的菱形), 颜色(红色和蓝色), 类型等于两者(对两个点进行绘图并将它们与线连接)以及y的名称轴(均方误差)。你还可以在图的右上角放置图例。
matplot(1:mtry, cbind(test.err, oob.err), pch = 23, col = c("red", "blue"), type = "b", ylab="Mean Squared Error")
legend("topright", legend = c("OOB", "Test"), pch = 23, col = c("red", "blue"))
理想情况下, 这两条曲线应对齐, 但似乎测试误差要低一些。但是, 这些测试误差估计中存在很多可变性。由于袋外误差估计是在一个数据集上计算的, 而测试误差估计是在另一个数据集上计算的, 因此这些差异在标准误差范围内非常好。
注意, 红色曲线平滑地位于蓝色曲线上方吗?这些误差估计值非常相关, 因为mtry = 4的randomForest与mtry = 5的randomForest非常相似。这就是每个曲线都非常平滑的原因。你看到的是, 至少对于测试错误, mtry 4似乎是最佳选择。袋外误差的mtry值等于9。
因此, 使用很少的层, 你就可以使用随机森林来拟合非常强大的预测模型。为何如此?左侧显示了单棵树的性能。书包外的均方误差为26, 而你下降到约15(略高于一半)。这意味着你将错误减少了一半。同样, 对于测试错误, 你将错误从20减少到了12。
助推
与随机森林相比, 助推植物会长出较小且较矮的树木, 并且会产生偏差。你将在R中使用软件包GBM(梯度增强建模)。
require(gbm)
GBM要求分配高斯分布, 因为你将要进行平方误差损失。你将要向GBM索取10, 000棵树, 这听起来很多, 但这些树都是浅树。交互深度是拆分的数量, 因此每棵树中需要4个拆分。收缩率为0.01, 这就是你要收缩的树后退量。
boost.boston = gbm(medv~., data = boston[train, ], distribution = "gaussian", n.trees = 10000, shrinkage = 0.01, interaction.depth = 4)
summary(boost.boston)
摘要功能提供了可变的重要性图。似乎有两个具有较高相对重要性的变量:rm(房间数)和lstat(社区中经济地位较低的人们的百分比)。让我们绘制这两个变量:
plot(boost.boston, i="lstat")
plot(boost.boston, i="rm")
第一个图显示, 郊区地位较低的人口比例越高, 房价的价值就越低。第二幅图显示了与房间数量的反向关系:房屋中的平均房间数量随着价格的上涨而增加。
现在是时候在测试数据集上预测增强模型了。让我们看一下测试性能与树数的关系:
首先, 从100到10, 000以100为步长构建树数网格。
然后, 你在增强模型上运行预测函数。它以n.trees作为参数, 并生成关于测试数据的预测矩阵。
矩阵的尺寸为206个测试观察值和100个不同树值的100个不同预测矢量。
n.trees = seq(from = 100, to = 10000, by = 100)
predmat = predict(boost.boston, newdata = boston[-train, ], n.trees = n.trees)
dim(predmat)
现在该为每个预测向量计算测试误差了:
predmat是矩阵, medv是向量, 因此(predmat-medv)是差异矩阵。你可以对这些平方差(均值)的列使用apply函数。这将为预测向量计算列方向均方误差。
然后, 使用与用于随机森林的参数相似的参数进行绘图。它会显示出上升的误差图。
boost.err = with(boston[-train, ], apply( (predmat - medv)^2, 2, mean) )
plot(n.trees, boost.err, pch = 23, ylab = "Mean Squared Error", xlab = "# Trees", main = "Boosting Test Error")
abline(h = min(test.err), col = "red")
随着树木数量的增加, 提升误差几乎下降了。这是一个证据, 表明增强不愿意过度拟合。让我们还将来自randomForest的最佳测试误差包括在图中。实际上, 对于randomForest而言, 增强会获得低于测试错误的合理数量。
总结
因此, 这是有关构建决策树模型的R教程的结尾:分类树, 随机森林和增强树。后两种是功能强大的方法, 你可以根据需要随时使用。以我的经验, 增强通常优于RandomForest, 但RandomForest更易于实现。在RandomForest中, 唯一的调整参数是树的数量。在进行增强时, 除了树木数量(包括收缩和交互作用深度)以外, 还需要更多的调整参数。
如果你想了解更多信息, 请务必阅读我们的R机器学习工具箱课程。
 srcmini
srcmini
评论前必须登录!
注册