本文概述
尽管机器学习领域随着越来越复杂的技术的发展而迅速发展, 但很少关注需要同时预测多个响应的高维多任务问题。本教程将向你展示图导融合LASSO(GFLASSO)在单个正则化线性回归框架下预测多个响应的功能。
介绍
在监督学习中, 通常旨在根据一组样本或观察值中的一组解释变量或预测变量来预测因变量或响应变量。正则化方法引入了防止高维数据过度拟合的惩罚, 特别是当预测变量的数量超过观测数量时。将这些惩罚加到目标函数中, 以使非信息性预测变量的系数估计(对误差最小化的贡献很小)本身也最小化。最小绝对收缩和选择算子(LASSO)[1]就是这样一种方法。
什么是LASSO?
与普通最小二乘法(OLS)相比, LASSO能够将系数估算值(β)缩小为恰好为零, 从而排除了无用的预测变量并通过
$$ argmin_ \ beta \ sum_n(y_n- \ hat {y_n})^ 2+ \ lambda \ sum_ {j} | \ beta_ {j} | $$
其中n和j分别表示任何给定的观察值和预测值。残差平方和(RSS)是OLS中唯一使用的术语, 可以等效地用代数形式$ RSS = \ sum_n(y_n- \ hat {y_n})^ 2 =(yX \ beta)^ T。( yX \ beta)$。 LASSO罚分是λ∑j |βj|, 系数估计的L1范数由λ加权。
为什么使用图形引导的熔融LASSO(GFLASSO)?
如果你打算从一组通用的预测变量中一次预测多个相关响应, 该怎么办?虽然你可以有效地使用多个独立的LASSO模型, 每个响应一个模型, 但将这些预测与响应之间的关联强度进行协调会更好。这是因为这样的协调抵消了特定于响应的变化, 该变化包括噪声-GFLASSO的关键强度。
原始文章中提供了一个很好的例子, 作者解决了543例患者中34种遗传标记与53种哮喘性状之间的关联[2]。
什么是GFLASSO?
令X为n××p的矩阵, 其中n个观测值和p个预测变量, 而Y为n××k的矩阵, n个观测值和k个响应相同, 例如, 在73个国家/地区有1390个不同的电子产品购买记录, 以预测在所有73个国家/地区对50部Netflix作品进行收视率排名。
可以很好地建模成对的高维数据集的模型包括正交双向偏最小二乘(O2PLS), 典范相关分析(CCA)和协惯性分析(CIA), 所有这些都涉及矩阵分解[3]。另外, 由于这些模型基于潜在变量(即基于原始预测变量的预测), 因此计算效率是以可解释性为代价的。
但是, 这种权衡并不总能奏效, 并且可以在考虑到响应之间关系的统一回归框架中, 根据X中选定特征对k个单个响应的直接预测来还原。
从数学上讲, GFLASSO借用了上面讨论的LASSO [1]的正则化, 并在基于k的关系图上建立了模型, 该关系由k×k相关矩阵(即你先前阅读的”关联强度”)量化)。结果, 将通过所选预测变量的相似(或不同)子集来解释相似(或不同)的响应。
更正式地说, 按照原始手稿[2]中使用的符号, GFLASSO的目标函数是
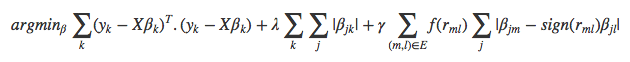
其中, 在所有k个响应中, ∑k(yk-X **βk)T.(yk-X **βk)提供RSS和λ∑k∑j |βj** k |。从LASSO借来的正则化罚分, 由参数λ加权并作用于每个预测变量j的系数β。 GFLASSO的新颖之处在于
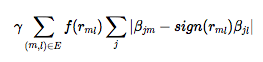
γ加权的融合罚分确保从任何预测变量j和成对的响应m和l来的系数βj** m和βj** l之间的绝对差将越小(分别越大), 则正值(原(更负)他们的成对相关性, 无论是否转换, f(rm ** l)。这种融合惩罚有利于全局有意义的响应变化, 而不是每个响应的噪声。当成对相关接近于零时, 它不执行任何操作, 在这种情况下, 你将得到纯LASSO。所有k个响应的基础相关结构(可以表示为加权网络结构)默认为绝对相关f(rm ** l)= | rm ** l |。但可以转换为具有任何用户指定功能的GFLASSO变体, 例如
- 平方相关, f(rm ** l)= rm ** l2(加权)
- 阈值相关, $ f(r_ {ml})= \ begin {cases} 1, &\ mbox {if} r_ {ml}> \ tau \\ 0, &\ mbox {否则} \ end {cases} $(未加权)
还有更多的创新空间。尽管与1.和默认的绝对相关性[2]相比, 2.的计算强度要小得多, 但它确实需要预定义的截止时间, 例如τ== 0.8。
综上所述, 要拟合GFLASSO模型, 你将需要一个预测矩阵X, 一个响应矩阵Y和一个描述Y中所有响应对之间关联强度的相关矩阵。请注意, GFLASSO产生β的ap×k矩阵, 与LASSO(p×1)不同, 该系数矩阵带有任何给定响应k和预测变量j之间的关联。
开始吧
我和Kris Sankaran一直在研究一个实验性R程序包, 该程序包实现了GFLASSO以及交叉验证和绘图方法。我们最近使用doParallel包实现了多线程, 从而提供了更快的交叉验证(CV)例程。
要在R中运行GFLASSO, 你需要安装devtools, 加载它并从我的GitHub存储库中安装gflasso软件包。该演示将在软件包bgsmtr中包含的数据集上进行。我还建议安装corrplot和pheatmap以可视化结果。
# Install the packages if necessary
#install.packages("devtools")
#install.packages("bgsmtr")
#install.packages("corrplot")
#install.packages("pheatmap")
library(devtools)
library(bgsmtr)
library(corrplot)
library(pheatmap)
#install_github("monogenea/gflasso")
library(gflasso)
模拟
你可以轻松地运行CV函数cv_gflasso()的帮助页面中概述的仿真。默认情况下, CV在λ∈{0, 0.1, 0.2, …, 0.9, 1}和γ∈之间的所有可能对上计算5倍CV的单次重复的均方根误差(RMSE) {0, 0.1, 0.2, …, 0.9, 1}, 调整网格。
请注意, 用户提供的错误功能也将起作用!
除了固有的统计假设和速度性能外, 调整网格范围的选择还很大程度上取决于X和Y中所有列的均心和单位方差缩放比例, 因此请确保你事先这样做。
在以下示例中, 你将不需要它, 因为你将从标准正态分布中抽取随机样本。你可以尝试从不加权的相关网络中得出融合惩罚, 其截止值为r> 0.8:
?cv_gflasso
set.seed(100)
X <- matrix(rnorm(100 * 10), 100, 10)
u <- matrix(rnorm(10), 10, 1)
B <- u %*% t(u) + matrix(rnorm(10 * 10, 0, 0.1), 10, 10)
Y <- X %*% B + matrix(rnorm(100 * 10), 100, 10)
R <- ifelse(cor(Y) > .8, 1, 0)
system.time(testCV <- cv_gflasso(X, Y, R, nCores = 1))
## [1] 1.826146 1.819430 1.384595 1.420058 1.408619
## user system elapsed
## 45.808 3.070 55.271
system.time(testCV <- cv_gflasso(X, Y, R, nCores = 2))
## [1] 1.595413 1.492953 1.469917 1.366832 1.441642
## user system elapsed
## 22.231 1.698 26.441
cv_plot_gflasso(testCV)

在此模拟中, 使RMSE最小的λ(行)和γ(列)的最优值分别为0.3和0.8, 这确实体现了所施加的关系。
提示:尝试使用其他度量标准(确定系数(R2))重新运行此示例。使用R2的一个主要优点是它的范围是0到1。
请记住, 当你提供自定义拟合优度函数err_fun()时, 必须使用参数err_opt定义是最大化还是最小化所得度量。
以下示例旨在使用具有平方相关系数(即f(rm ** l)= rm ** l2)的加权关联网络来最大化R2。如果你拥有2个以上的内核, 则最好更改nCores参数并提高它!
# Write R2 function
R2 <- function(pred, y){
cor(as.vector(pred), as.vector(y))**2
}
# X, u, B and Y are still in memory
R <- cor(Y)**2
# Change nCores, if you have more than 2, re-run CV
testCV <- cv_gflasso(X, Y, R, nCores = 2, err_fun = R2, err_opt = "max")
## [1] 0.6209191 0.7207394 0.7262781 0.7193907 0.6303187
cv_plot_gflasso(testCV)

现在, 最佳参数λ和γ分别为0.6和0.3。
另外, 请注意cv_gflasso对象包含具有四个元素的单个列表:网格所有单元上度量的均值($ mean)和标准误差($ SE), 最佳λ和γ参数($ optimal)以及名称拟合优度函数($ err_fun)。来自本示例的交叉验证模型显然同时支持稀疏性(λ)和融合(γ)。
最后, 请记住, 你可以通过分别将delta_conv和iter_max传递给AdditionalOpts来微调其他参数, 例如Nesterov的梯度收敛阈值δ和最大迭代次数。这些将在以下示例中使用。
确定与GFLASSO的SNP神经影像关联
为了说明GFLASSO在一个相对较高维度的问题中的简单性和鲁棒性, 你接下来将对从阿尔茨海默氏病神经影像计划(ADNI-1)数据库获得的bgsmtr_example_data数据集进行建模。
这是一个由3个元素组成的列表对象, 是bgsmtr软件包的一部分, 该软件包由15个结构性神经影像学措施和632个受试者的样本确定的486个单核苷酸多态性(SNP, 遗传标记)组成。重要的是, 这486个SNP涵盖了33个被认为与阿尔茨海默氏病相关的基因。
你的任务是利用SNP的相关结构来预测SNP数据的形态学, 神经影像学指标。
让我们开始整理数据并探索所有神经影像功能之间的相互依存关系:
data(bgsmtr_example_data)
str(bgsmtr_example_data)
## List of 3
## $ SNP_data : int [1:486, 1:632] 2 0 2 0 0 0 0 1 0 1 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:486] "rs4305" "rs4309" "rs4311" "rs4329" ...
## .. ..$ : chr [1:632] "V1" "V2" "V3" "V4" ...
## $ SNP_groups : chr [1:486] "ACE" "ACE" "ACE" "ACE" ...
## $ BrainMeasures: num [1:15, 1:632] 116.5 4477.9 28631.9 34.1 -473.4 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:15] "Left_AmygVol.adj" "Left_CerebCtx.adj" "Left_CerebWM.adj" "Left_HippVol.adj" ...
## .. ..$ : chr [1:632] "V1" "V2" "V3" "V4" ...
# Transpose, so that samples are distributed as rows, predictors / responses as columns
SNP <- t(bgsmtr_example_data$SNP_data)
BM <- t(bgsmtr_example_data$BrainMeasures)
# Define dependency structure
DS <- cor(BM)
# Plot correlation matrix of the 15 neuroimaging measures
corrplot(DS)

上图指出了神经影像特征之间的相互依赖性。现在尝试交叉验证GFLASSO(在一台笔记本电脑上可能要花费几个小时!), 然后确定SNP-神经影像关联。
请注意, 在下面的示例中, 指定了收敛容限和最大迭代次数。随意尝试不同的值!
system.time(CV <- cv_gflasso(X = scale(SNP), Y = scale(BM), R = DS, nCores = 2, additionalOpts = list(delta_conv = 1e-5, iter_max = 1e5)))
## [1] 1.550294 1.471637 1.470133 1.514425 1.504215
## user system elapsed
## 2611.492 323.441 51129.936
cv_plot_gflasso(CV)

通过用纯LASSO模型(γ= 0, 第一列), 纯融合最小二乘法(λ= 0, 第一行)和OLS(γ= 0和λ= 0, 左上角单元格)挑战GFLASSO, 我们可以得出结论本示例是使用非零惩罚权重并因此使用完整GFLASSO进行最佳建模的。取最佳CV参数(λ= 0.7和γ= 1)建立GFLASSO模型并解释所得的系数矩阵:
gfMod <- gflasso(X = scale(SNP), Y = scale(BM), R = DS, opts = list(lambda = CV$optimal$lambda, gamma = CV$optimal$gamma, delta_conv = 1e-5, iter_max = 1e5))
colnames(gfMod$B) <- colnames(BM)
pheatmap(gfMod$B, annotation_row = data.frame("Gene" = bgsmtr_example_data$SNP_groups, row.names = rownames(gfMod$B)), show_rownames = F)

上图显示了很大一部分系数为零或接近零的值。尽管在基因上没有明显的SNP聚类(请参阅逐行注释, 注意图例不完整), 但某些SNP与性状之间存在明确的关联。
为了确定是否存在非随机预测机制, 你可以在对X或Y中的值进行置换后, 再次重复该过程。实验工作可以帮助阐明所选SNP的因果关系和机制。例如, 影响蛋白质序列和结构的SNP破坏了Alzheimer病基础的β-淀粉样蛋白斑的清除。
包起来
在对多个响应进行建模时, GFLASSO同时使用正则化和融合, 从而便于识别预测变量(X)和响应(Y)之间的关联。当处理来自极少观测值的高维数据时, 它是最佳选择, 因为它比竞争方法慢得多。例如, 稀疏的条件高斯图形模型[4]和贝叶斯群稀疏多任务回归模型[5]可能主要是为了提高性能。尽管如此, GFLASSO是高度可解释的。最近, 我以组学整合方法使用了GFLASSO, 以发现玉米中的新脂质基因[6]。
克里斯和我很高兴收到你的来信。目前, 该项目由Kris在回购krisrs1128 / gflasso下并通过我的项目进行维护, 尽管经常更改, 但仍在monogenea / gflasso下进行。随时写信给我(francisco.lima278@gmail.com), 欢迎所有反馈。
编码愉快!
参考文献
- Robert Tibshirani(1994)。通过套索进行回归收缩和选择。皇家统计学会杂志, 58, 267-288。
- 金世yo, 宋庆亚, 邢爱宝(2009)。定量特征网络关联分析的多元回归方法。生物信息学, 25, 12:i204–i212。
- Chen Meng, Oana A.Zeleznik, Gerhard G.Thallinger, Bernhard Kuster, Amin M.Gholami, AedínC.Culhane(2016)。用于多组学数据集成分析的降维技术。 《生物信息学简报》, 第17期, 第4期:628-641。
- 张玲雪, 金世yo(2014)。使用eQTL数据集在SNP扰动下学习基因网络。 PLoS Comput Biol, 10, 2:e1003420。
- Keelin Greenlaw, Elena Szefer, Jinko Graham, Mary Lesperance, Farouk S.Nathoo(2017)。用于成像遗传学的贝叶斯群稀疏多任务回归模型。生物信息学, 33, 16:2513–2522。
- 弗朗西斯科·德·阿布雷乌·利马(Francisco de Abreu e Lima), 李坤, 温伟伟, 严建兵, 佐兰·尼科洛斯基, 洛萨·威尔米泽(Lothar Willmitzer), 雅里夫·布罗特曼(Yariv Brotman)(2018)。利用时间分辨的多组学数据阐明玉米中的脂质代谢。植物学报, 93, 6:1102-1115。
 srcmini
srcmini
评论前必须登录!
注册