R中的网络分析：集中度度量

本文概述

• 中心性的定义
• 集中度度量：类型
• 如何选择最佳的集中度度量
• 本文总结

执行网络分析时, 你要做的最重要的事情之一就是确定节点在社交网络中的中心位置。换句话说, 如果你有一个要分析的网络, 则需要找出哪个节点对其他节点影响最大。本教程将完全涵盖该内容。在其中, 你将了解有关以下主题的更多信息：

• 中心性的定义是什么？
• 集中度措施有哪些类型？
• 根据网络拓扑指定最佳集中度度量的过程是什么？

中心性的定义

如今, 对于每个想从事网络科学工作的研究人员而言, 学习如何找到网络的基本节点都是至关重要的。随着你的前进, 在不同科学领域中的网络将变得更加庞大和复杂。因此, 仔细地分析每个节点既费钱又费时, 而且某种程度上是不可能的。中心性描述回答了以下问题：”哪个节点是网络中最重要的节点？”。

根据网络对每个顶点的影响将数值分配给网络的每个顶点的函数。节点的重要性取决于其在网络中的位置。根据网络的类型, 你可以描述重要性的含义。在社交网络或城市网络的关键基础设施节点中, 可以将其识别为有效人员。

集中度度量：类型

中心性索引可以分为本地和全局分类。

地方集中措施

局部集中度度量的一个示例是集中度, 它计算每个节点保持的链接数, 并指向可以快速连接到更广泛网络的个人。这是一项本地措施, 因为它没有考虑网络的其余部分, 你对其价值的重视程度很大程度上取决于网络的规模。

要计算像度这样的流行集中度度量, 你可以使用igraph软件包。你可以借助library()函数使其可用：

library(igraph)

在执行任何中心性计算之前, 你需要具有网络。为此, 你可以使用诸如Erdos-Renyi模型之类的随机算法之一来构建样本图。

两位伟大的数学家Paul Erdos和Alfred Renyi于1959年引入了Erdos-Renyi模型。生成随机图是很有用的, 在该图中每对节点以相等的概率值连接在一起以形成一条边。在此随机图模型中, 大多数节点的连接数近似相等, 并且该模型的度分布通常为二项式或泊松分布。这可以用在概率方法中, 以证明具有各种属性的图的存在, 或详细说明与真实网络的结构比较。

要查看Erdos-Renyi模型的示例, 可以使用igraph包中的sample_gnm()函数。

# n = number of nodes, m = the number of edges
erdos.gr <- sample_gnm(n=10, m=25) 

plot(erdos.gr)

它是一个无向网络, 与双向图相反, 该图具有双向边, 而有向图则考虑了从一个顶点到另一个顶点的边方向, 其中包含10个节点和25个边。

可以使用centr_degree()函数计算此图的度中心度：

degree.cent <- centr_degree(erdos.gr, mode = "all")
degree.cent$res

##  [1] 2 3 5 6 7 7 6 3 6 5

如图所示, 在整个样本网络中, 节点1的中心度值最高。

全球中心措施

另一方面, 全球中心度措施考虑了整个网络。紧密度中心度是最广泛使用的全球中心度度量之一。该度量基于每个节点与网络中所有其他节点的接近程度对它们进行评分。

它计算所有节点之间的最短路径, 然后根据其最短路径的总和为每个节点分配分数, 这对于查找最能快速影响整个网络的个人很有用。

建议使用”紧密度”在单个群集中查找中心顶点。你可以通过igraph包中的closeness()函数进行计算。

closeness.cent <- closeness(erdos.gr, mode="all")
closeness.cent

##  [1] 0.05882353 0.06250000 0.07142857 0.08333333 0.09090909 0.09090909
##  [7] 0.08333333 0.06250000 0.08333333 0.07692308

根据接近性中心性结果, 与度中心性不同, 节点1和9在整个网络中具有最高中心性值。这意味着这些节点在网络流中具有同等重要的作用。

如何选择最佳的集中度度量

尽管可以使用不同类型的集中度度量来确定网络中最有影响力的节点, 但是在网络科学中还没有共识管道可以为给定的网络选择和实施最佳量身定制的度量。

为了便于说明, 下图显示了两个集中度度量(称为”子图集中度”和”拓扑系数”)之间的散点图。红线表示这两个中心性措施之间存在强烈的负相关性。

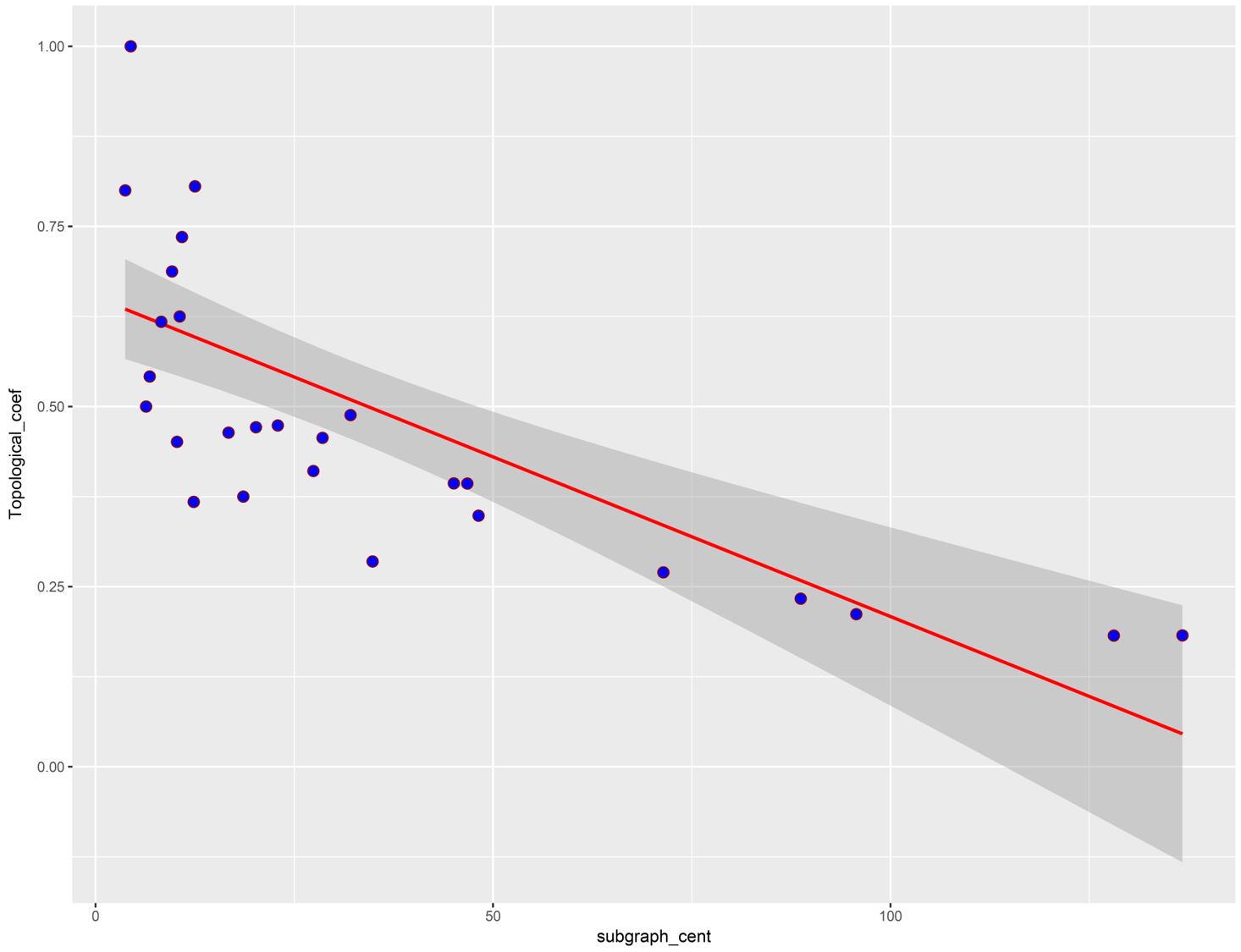
你可以从上述表示得出结论, 由于这两个中心具有相反的关系, 它们可以根据不同的模式区分网络中的中心节点, 因此中心性计算的结果将根据中心性类型而有所不同。

当前有140多个基准可用来标识中心顶点, 但是应该使用哪一个基准来计算影响节点？

此外, 由于网络的拓扑特征会影响中心度计算的结果, 因此你必须根据网络聚合来选择具有最高影响力顶点信息级别的条件。

CINNA(网络分析中的中央信息节点)是一个R软件包, 用于计算, 分析和比较提交给CRAN存储库的集中度度量。

若要查看如何使用此程序包, 请先使用程序包中称为Zachary的数据集之一。此数据集说明了大学空手道俱乐部成员之间的友谊：

library(CINNA)

data("zachary")

plot(zachary)

这是一个无向图, 具有34个顶点和78个边。请记住, 无向图是指边缘没有方向的图：它们是双向的。例如：A <-> B == B <-> A。

要根据图结构确定可计算的中心性类型, proper_centralities()函数可能会很有用。

pr_cent<-proper_centralities(zachary)

##  [1] "subgraph centrality scores"                      
##  [2] "Topological Coefficient"                         
##  [3] "Average Distance"                                
##  [4] "Barycenter Centrality"                           
##  [5] "BottleNeck Centrality"                           
##  [6] "Centroid value"                                  
##  [7] "Closeness Centrality (Freeman)"                  
##  [8] "ClusterRank"                                     
##  [9] "Decay Centrality"                                
## [10] "Degree Centrality"                               
## [11] "Diffusion Degree"                                
## [12] "DMNC - Density of Maximum Neighborhood Component"
## [13] "Eccentricity Centrality"                         
## [14] "eigenvector centralities"                        
## [15] "K-core Decomposition"                            
## [16] "Geodesic K-Path Centrality"                      
## [17] "Katz Centrality (Katz Status Index)"             
## [18] "Kleinberg's authority centrality scores"         
## [19] "Kleinberg's hub centrality scores"               
## [20] "clustering coefficient"                          
## [21] "Lin Centrality"                                  
## [22] "Lobby Index (Centrality)"                        
## [23] "Markov Centrality"                               
## [24] "Radiality Centrality"                            
## [25] "Shortest-Paths Betweenness Centrality"           
## [26] "Current-Flow Closeness Centrality"               
## [27] "Closeness centrality (Latora)"                   
## [28] "Communicability Betweenness Centrality"          
## [29] "Community Centrality"                            
## [30] "Cross-Clique Connectivity"                       
## [31] "Entropy Centrality"                              
## [32] "EPC - Edge Percolated Component"                 
## [33] "Laplacian Centrality"                            
## [34] "Leverage Centrality"                             
## [35] "MNC - Maximum Neighborhood Component"            
## [36] "Hubbell Index"                                   
## [37] "Semi Local Centrality"                           
## [38] "Closeness Vitality"                              
## [39] "Residual Closeness Centrality"                   
## [40] "Stress Centrality"                               
## [41] "Load Centrality"                                 
## [42] "Flow Betweenness Centrality"                     
## [43] "Information Centrality"

结果包含一个列表, 该列表指示43个流行的中心名称, 这些名称专门用于无方向性, 无权结构。

让我们从列表中选择前五个中心度度量, 然后将它们传递给calculate_centralities()函数, 因为所有可计算中心度的计算将很耗时。

在下一步中, 你将使用主成分分析(PCA)算法来区分信息量最大的中心度度量。

请记住, PCA是分别用于线性分析的降维技术。

在此分析步骤中, 每个中心性度量均充当变量。因此, 与主成分相关的中心性在识别中心节点中最重要。 PCA的贡献标准显示了变量如何影响主要成分。

换句话说, 变量的贡献说明了相对于主成分的可变性(百分比)。多亏了PCA方法中的这一标准, 你可以检测到哪些中心具有有关中心节点的更多信息, 因此, 哪个中心可以更准确地描述网络的有影响力的顶点。因此, 中心的分类贡献指数可以如下所示。

下面, 你将使用管道运算符％>％连续应用这两个最近的步骤：

calculate_centralities(zachary, include = pr_cent[1:5])%>%
  pca_centralities(scale.unit = TRUE)

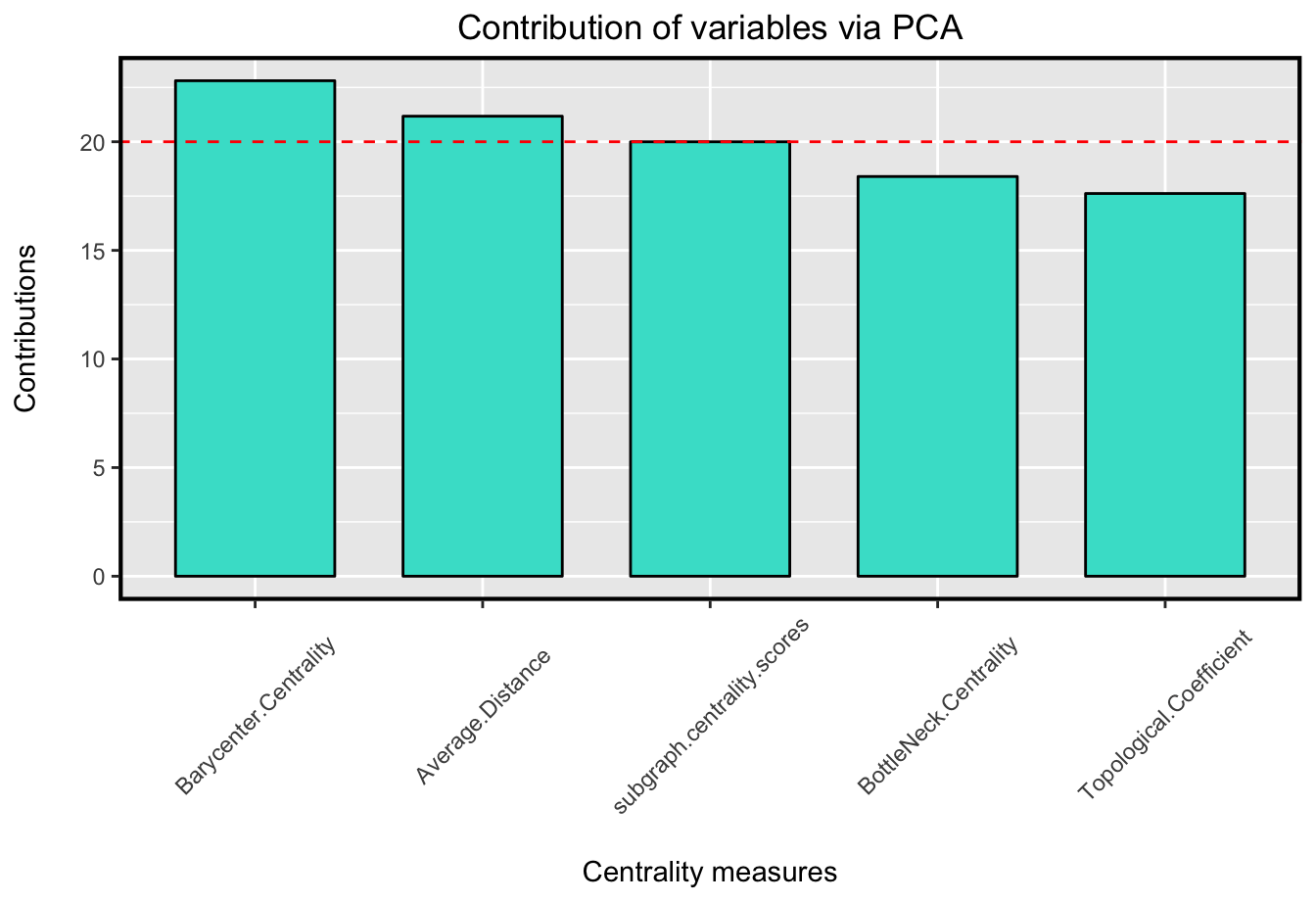
如图所示, 重心中心性在五个中心性指数中贡献最大。

换句话说, 它在计算的中心度度量中具有有关影响节点的最多信息。因此, 它可以比选择的中心性更准确地确定中心节点。

如下图所示, 其中每个节点的大小表示其相应的中心度值。

visualize_graph( zachary , centrality.type="Barycenter Centrality")

因此, 节点1是所有节点中最中心的节点。

本文总结

总而言之, 为了量化网络的连通性, 建议将PCA应用于一些中心性度​​量, 这些度量可以根据网络结构进行计算, 并选择最有用的度量进行计算并解释相对于网络的最大贡献量。它们相应的主要成分。

在本教程中, 你首先描述了中心性定义并讨论了一些流行的定义。然后, 你强调, 由于网络的全局属性会影响中心组件检测, 因此网络的影响节点会有所不同, 具体取决于网络拓扑。

在下一步中, 你使用了CINNA软件包, 该软件包提供了在网络中应用集中性分析的所有必需功能。使用此软件包, 你可以在网络上进行集中度分析, 而无需进行任何其他工作。此外, 这显着提高了中心节点确定的准确性。

如果你想直接研究该主题并了解其工作原理, 请查阅本白皮书以及本白皮书。

如果你对以上问题有任何疑问或疑虑, 请随时通过Minoo_Ashtiani与我联系。