本文概述
逻辑回归是机器学习从统计领域借用的另一种技术。这是一种使用一个或多个解释变量对二项式结果建模的强大统计方法。它通过使用对数函数(即累积对数分布)估计概率来测量分类因变量和一个或多个自变量之间的关系。
该R教程将指导你完成逻辑回归的简单执行:
首先, 你将探讨逻辑回归的理论:你将进一步了解线性回归的差异以及逻辑回归模型的外观。你还将发现多项式和有序逻辑回归。
接下来, 你将解决R中的逻辑回归:不仅将探索数据集, 还将使用R中强大的glm()函数拟合逻辑回归模型, 评估结果并解决过度拟合问题。
提示:如果你有兴趣将线性回归的技能提高到一个新的水平, 还可以考虑srcmini的多元和逻辑回归课程!
回归分析:简介
顾名思义, 逻辑回归是一种回归分析技术。回归分析是一组统计过程, 可用于估计变量之间的关系。更具体地说, 你使用这套技术来建模和分析因变量与一个或多个自变量之间的关系。回归分析可帮助你了解自变量之一的典型值在调整其中一个自变量而其他变量保持固定时如何变化。
正如你已经阅读的, 有各种回归技术。你可以通过三个方面来区分它们:自变量的数量, 因变量的类型和回归线的形状。
线性回归
线性回归是最广为人知的建模技术之一。简而言之, 它使你可以使用线性关系来预测给定值$ X $的直线的$ Y $(平均)数值。该线称为”回归线”。
结果, 线性回归模型为$ y = ax + b $。该模型假定响应变量$ y $是定量的。但是, 在许多情况下, 响应变量是定性的, 或者说是分类的。例如, 性别是定性的, 具有男性或女性的价值观。
预测观察的定性响应可以称为对该观察进行分类, 因为它涉及将观察分配给一个类别或类别。另一方面, 通常用于分类的方法首先预测定性变量的每个类别的概率, 作为进行分类的基础。
线性回归不能预测概率。例如, 如果你使用线性回归对二进制响应变量进行建模, 则结果模型可能不会将预测的Y值限制在0和1之内。这就是逻辑回归的作用所在, 你将获得反映该概率的概率的分数。事件发生。

逻辑回归
Logistic回归是分类技术的一个实例, 可用于预测定性反应。更具体地说, 逻辑回归建模$ gender $属于特定类别的概率。
这意味着, 如果你尝试进行性别分类, 其中响应$ gender $属于男性或女性两个类别之一, 则将使用逻辑回归模型来估算$ gender $属于特定类别的概率类别。
例如, 给定$ longhair $的$ gender $概率可以写成:
$ Pr(性别=女性|长发)$
$ Pr(gender = female | longhair)$(缩写为$ p(longhair)$)的值将介于0和1之间。然后, 对于$ long hair $的任何给定值, 可以对$ gender进行预测$。
给定$ X $作为解释变量, 而$ Y $作为响应变量, 那么应该如何对$ p(X)= Pr(Y = 1 | X)$和$ X $之间的关系建模?线性回归模型将这些概率表示为:
p(X)=β0+β1X
这种方法的问题是, 只要一条直线适合于编码为$ 0 $或$ 1 $的二进制响应, 原则上我们就可以始终预测$ p(X)<0 $对于$ X $的某些值$ p(X)> 1 $。
为避免此问题, 可以使用逻辑函数对$ p(X)$建模, 该函数对于$ X $的所有值给出在$ 0 $和$ 1 $之间的输出:
$$ p(X)= \ frac {e ^ {\ beta_ {0} + \ beta_ {1} X}} {1 + e ^ {\ beta_ {0} + \ beta_ {1} X}} $$
逻辑函数将始终生成S形曲线, 因此无论$ X $的值如何, 我们都将获得明智的预测。
上面的等式也可以重组为:
$$ \ frac {p(X)} {1-p(X)} = e ^ {\ beta_ {0} + \ beta_ {1} X} $$
数量$$ \ frac {p(X)} {1-p(X)} $$被称为优势比, 可以取介于$ 0 $和$ \ infty $之间的任何值。赔率比的值接近$ 0 $和$ \ infty $分别表示$ p(X)$的非常低和非常高的概率。
通过从上面的方程式获得双方的对数, 你将获得:
$$ log(\ frac {p(X)} {1-p(X)})= \ beta_ {0} + \ beta_ {1} X $$
左侧称为logit。在逻辑回归模型中, 将X增加一个单位会使logit改变β0。由于X的单位变化而导致p(X)的变化量取决于X的当前值。但是, 不管X的值如何, 如果β1为正, 则X的增加将与p(X)的增加有关。 , 如果β1为负, 则X的增加将与p(X)的减少相关。
系数β0和β1未知, 必须根据可用的训练数据进行估算。对于逻辑回归, 你可以使用最大似然法(一种强大的统计技术)。让我们再次参考你的性别分类示例。
你寻求β0和β1的估计值, 以便将这些估计值插入到p(X)模型中时, 所有女性个体的数字都接近于1, 而所有非女性个体的数字都接近于0。
可以使用称为似然函数的数学方程式来形式化这种直觉:
l(β0, β1)= p(X)(1 − p(X))
选择估计值β0和β1以使该似然函数最大化。一旦系数被估计, 给定任何具有$ long hair $的实例, 你就可以简单地计算出成为$ female $的概率。总的来说, 最大似然是拟合非线性模型的一种非常好的方法。
多项式Logistic回归
到目前为止, 由于你将实例分类为男性还是女性, 所以本教程仅专注于二项式Logistic回归。多项式Logistic回归模型是二项式Logistic回归模型的简单扩展, 在探索变量具有两个以上名义(无序)类别时使用。
在多项逻辑回归中, 将探索变量虚拟编码为多个1/0变量。除一个类别外, 所有类别都有一个变量, 因此, 如果有M个类别, 将有$ M-1 $个虚拟变量。每个类别的虚拟变量的类别值为1, 其他所有变量均为0。一个类别(参考类别)不需要自己的虚拟变量, 因为其他所有变量均为0即可唯一标识。
然后, 多项逻辑回归为这些虚拟变量中的每一个估计一个单独的二进制逻辑回归模型。结果是$ M-1 $二进制逻辑回归模型。与参考类别相比, 每种模型都传达预测变量对该类别成功概率的影响。
有序逻辑回归
除了多项逻辑回归外, 你还可以使用序数逻辑回归, 这是二项式物流回归的另一种扩展。序数回归用于预测具有”有序”多个类别和自变量的因变量。你已经看到了这种逻辑回归的名称, 因为”常规”的意思是”类别的顺序”。
换句话说, 它用于促进因变量(具有多个有序级别)与一个或多个自变量的交互。
例如, 你正在进行客户访谈, 以评估他们对我们新发布产品的满意度。你的任务是向受访者提问, 他们的答案在$满意$或$不满意$之间。为了很好地概括答案, 你可以在回答中添加级别, 例如$非常不满意$, $不满意$, $中性$, $满意$, $非常满意$。这有助于你观察类别中的自然顺序。
具有glm的R中的Logistic回归
在本部分中, 你将研究一个二进制逻辑回归的示例, 你将使用ISLR包(将为你提供数据集)和glm()函数(通常用于拟合广义线性)来解决该问题。模型, 将用于拟合逻辑回归模型。
加载数据中
首先要做的是安装和加载ISLR软件包, 其中包含你将要使用的所有数据集。
require(ISLR)
## Loading required package: ISLR
## Warning: package 'ISLR' was built under R version 3.3.2
在本教程中, 你将使用RStudio中的Smarket数据集。该数据集显示了2001年至2005年间标准普尔500指数的日收益率百分比。
探索数据
让我们探讨一下。 names()对于查看数据帧上的内容很有用, head()是前几行的一瞥, summary()也是有用的。
names(Smarket)
## [1] "Year" "Lag1" "Lag2" "Lag3" "Lag4" "Lag5"
## [7] "Volume" "Today" "Direction"
head(Smarket)
## Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction
## 1 2001 0.381 -0.192 -2.624 -1.055 5.010 1.1913 0.959 Up
## 2 2001 0.959 0.381 -0.192 -2.624 -1.055 1.2965 1.032 Up
## 3 2001 1.032 0.959 0.381 -0.192 -2.624 1.4112 -0.623 Down
## 4 2001 -0.623 1.032 0.959 0.381 -0.192 1.2760 0.614 Up
## 5 2001 0.614 -0.623 1.032 0.959 0.381 1.2057 0.213 Up
## 6 2001 0.213 0.614 -0.623 1.032 0.959 1.3491 1.392 Up
summary(Smarket)
## Year Lag1 Lag2
## Min. :2001 Min. :-4.922000 Min. :-4.922000
## 1st Qu.:2002 1st Qu.:-0.639500 1st Qu.:-0.639500
## Median :2003 Median : 0.039000 Median : 0.039000
## Mean :2003 Mean : 0.003834 Mean : 0.003919
## 3rd Qu.:2004 3rd Qu.: 0.596750 3rd Qu.: 0.596750
## Max. :2005 Max. : 5.733000 Max. : 5.733000
## Lag3 Lag4 Lag5
## Min. :-4.922000 Min. :-4.922000 Min. :-4.92200
## 1st Qu.:-0.640000 1st Qu.:-0.640000 1st Qu.:-0.64000
## Median : 0.038500 Median : 0.038500 Median : 0.03850
## Mean : 0.001716 Mean : 0.001636 Mean : 0.00561
## 3rd Qu.: 0.596750 3rd Qu.: 0.596750 3rd Qu.: 0.59700
## Max. : 5.733000 Max. : 5.733000 Max. : 5.73300
## Volume Today Direction
## Min. :0.3561 Min. :-4.922000 Down:602
## 1st Qu.:1.2574 1st Qu.:-0.639500 Up :648
## Median :1.4229 Median : 0.038500
## Mean :1.4783 Mean : 0.003138
## 3rd Qu.:1.6417 3rd Qu.: 0.596750
## Max. :3.1525 Max. : 5.733000
summary()函数为你提供Smarket数据框中每个变量的简单摘要。你会看到有很多滞后, 数量, 今天的价格和方向。你将使用Direction作为响应变量, 因为它显示了自前一天以来市场是上涨还是下跌。
可视化数据
数据可视化也许是总结和了解有关数据的最快, 最有用的方法。你将首先探索数字变量。
直方图提供了将数字变量分成条形图的条形图, 其高度显示了落入每个条形图的实例数。它们对于获得属性分布的指示很有用。
par(mfrow=c(1, 8))
for(i in 1:8) {
hist(Smarket[, i], main=names(Smarket)[i])
}
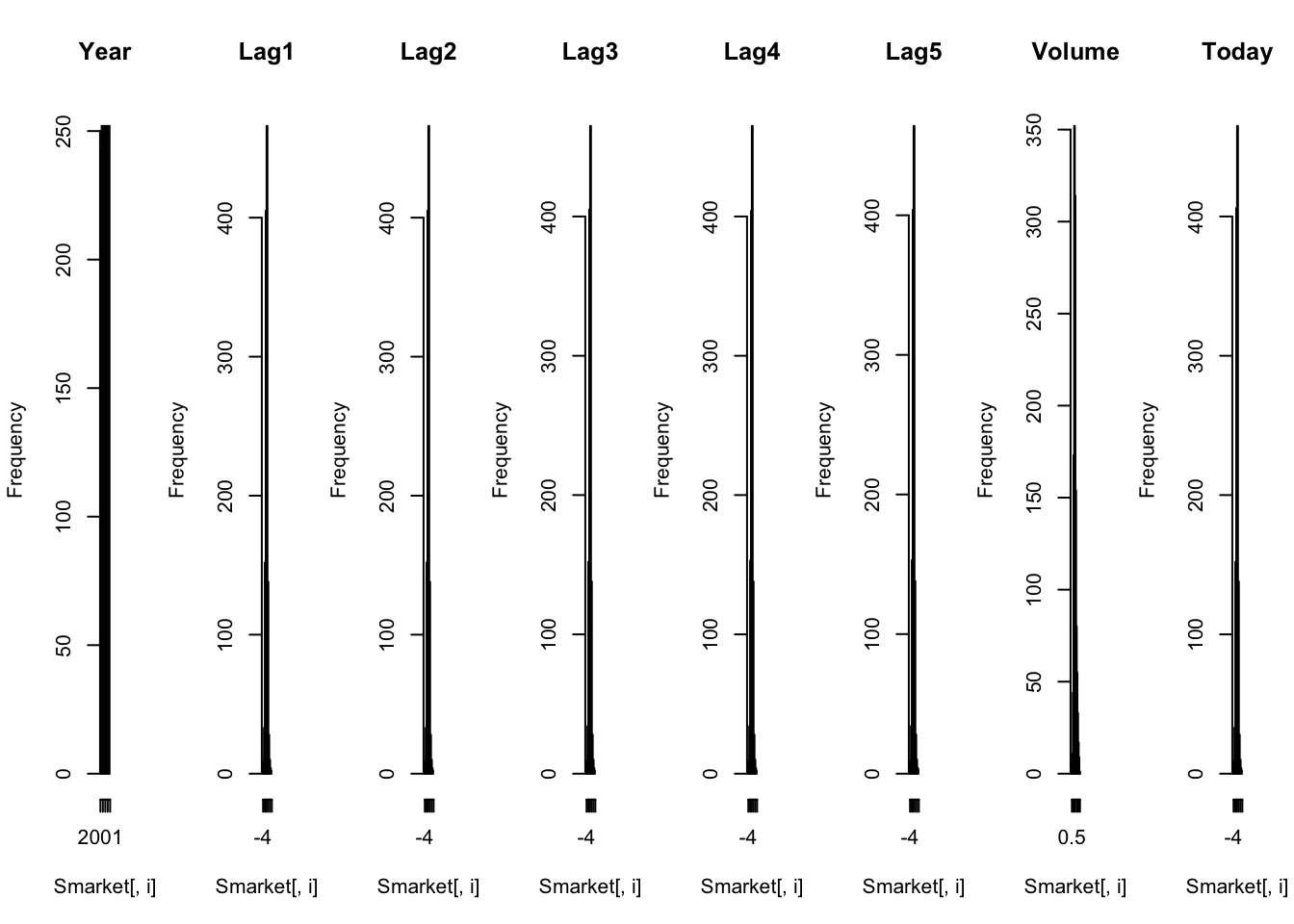
这很难看, 但是大多数变量都显示高斯或双高斯分布。
你可以使用箱形图和晶须图以不同的方式查看数据的分布。该框捕获了中间50%的数据, 该行显示了中间值, 图的晶须显示了合理的数据范围。晶须外的任何点都是异常值的理想选择。
par(mfrow=c(1, 8))
for(i in 1:8) {
boxplot(Smarket[, i], main=names(Smarket)[i])
}
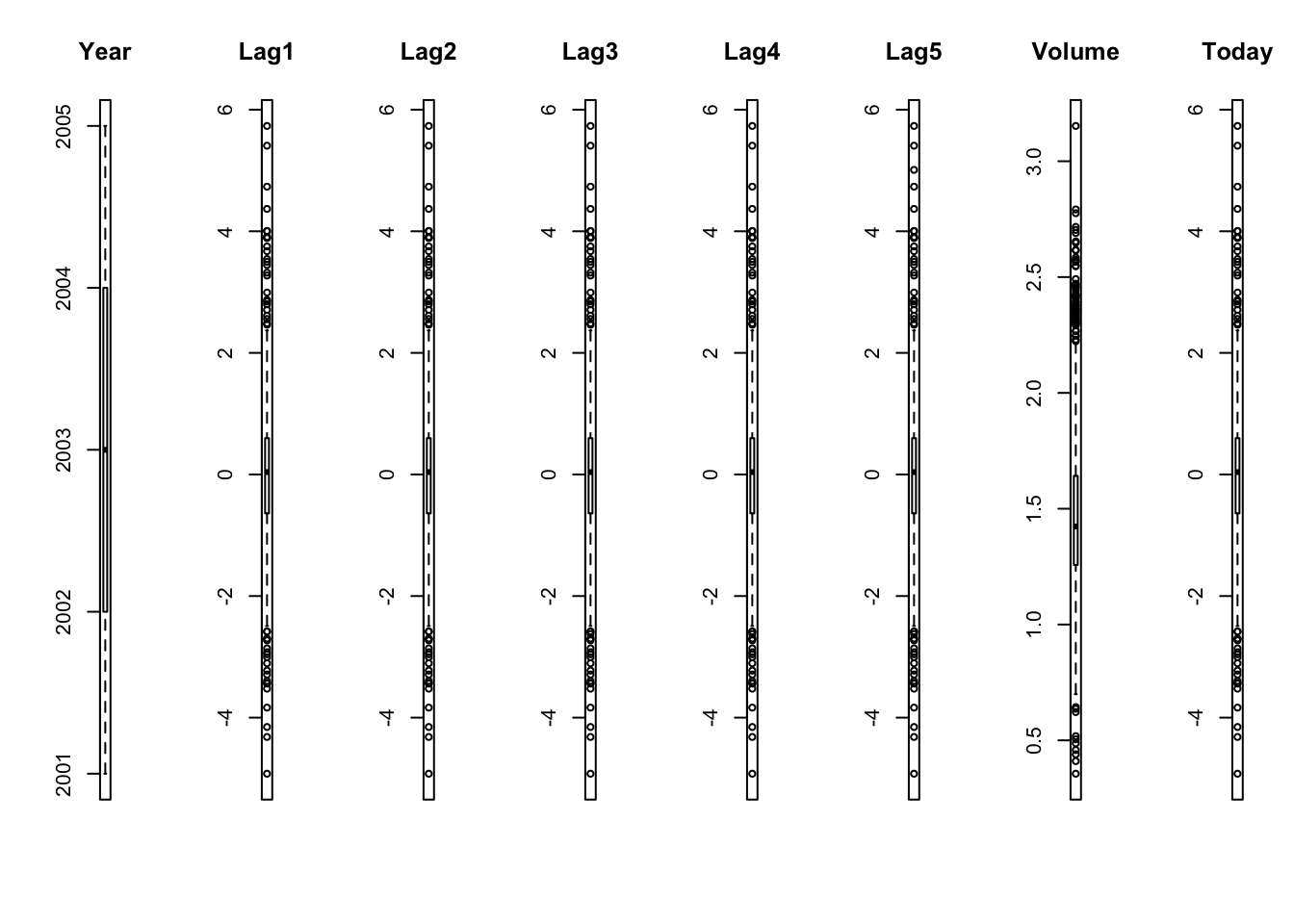
你可以看到”时滞”和”今天”的范围相似。否则, 没有任何异常值的迹象。
数据丢失对建模有很大影响。因此, 你可以使用缺失图来快速了解数据集中的缺失数据量。 x轴显示属性, y轴显示实例。水平线表示实例的缺失数据, 垂直块表示属性的缺失数据。
library(Amelia)
library(mlbench)
missmap(Smarket, col=c("blue", "red"), legend=FALSE)
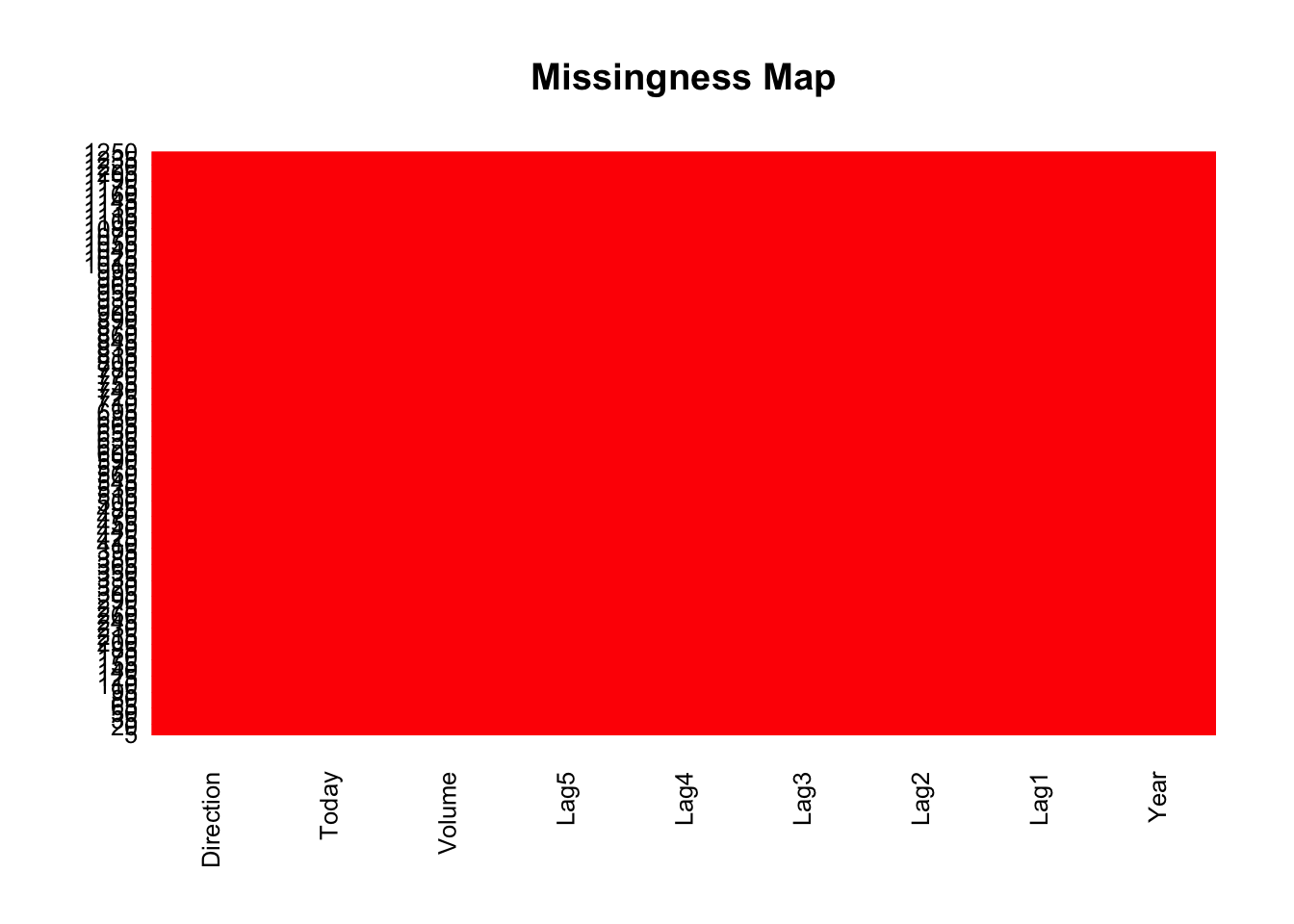
好吧, 我很幸运!此数据集中没有丢失的数据!
让我们开始计算每对数值变量之间的相关性。可以在相关矩阵图中绘制这些成对的相关性, 以了解哪些变量会一起变化。
library(corrplot)
correlations <- cor(Smarket[, 1:8])
corrplot(correlations, method="circle")
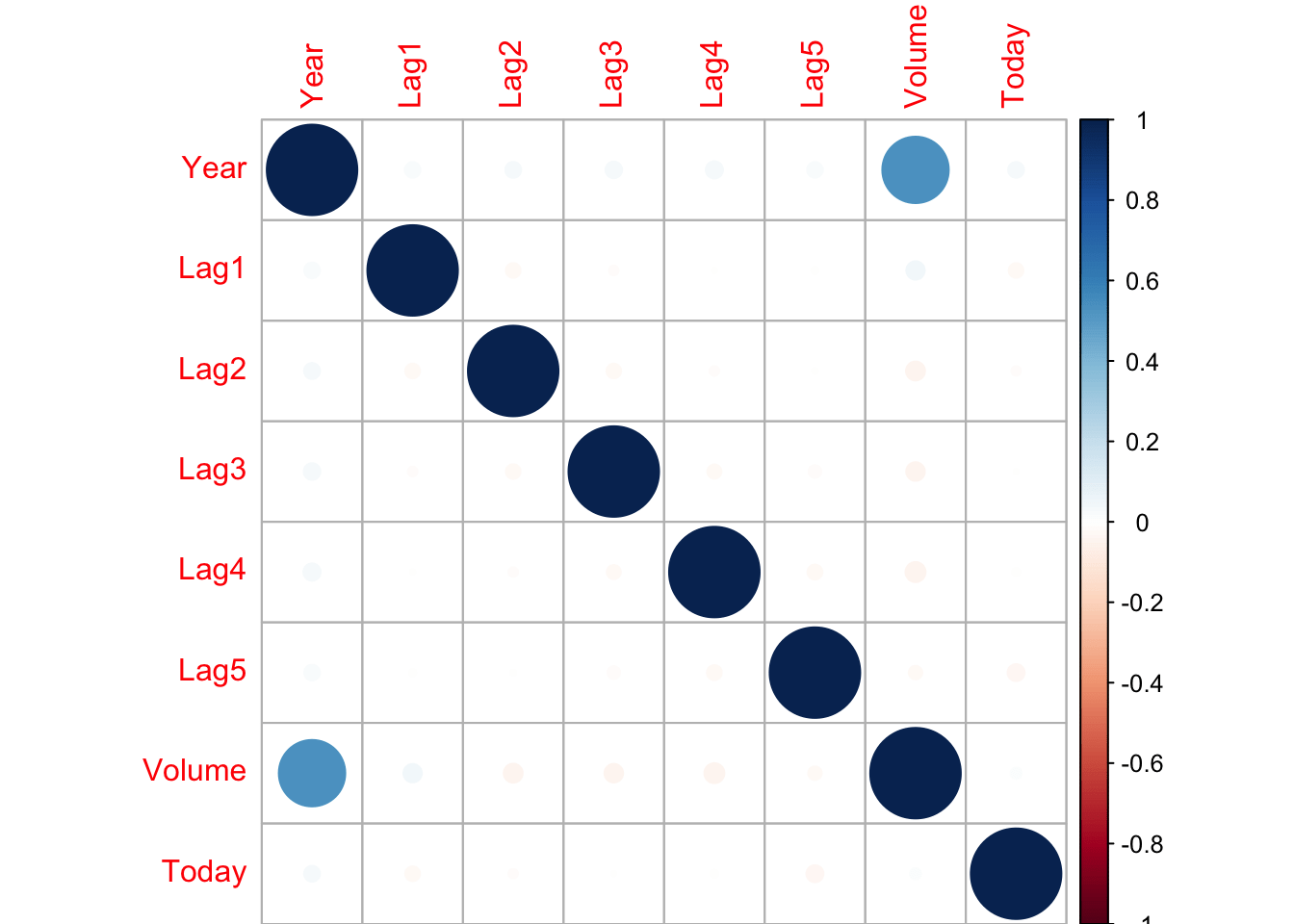
使用点表示法, 其中蓝色表示正相关, 红色表示负。点越大, 相关性越大。你会看到矩阵是对称的, 对角线是完全正相关的, 因为它显示了每个变量与其自身的相关性。不幸的是, 这些变量没有一个相互关联。
让我们绘制数据图。有一个pair()函数, 可将Smarket中的变量绘制到散点图矩阵中。在这种情况下, Direction(你的二进制响应)就是颜色指示器:
pairs(Smarket, col=Smarket$Direction)
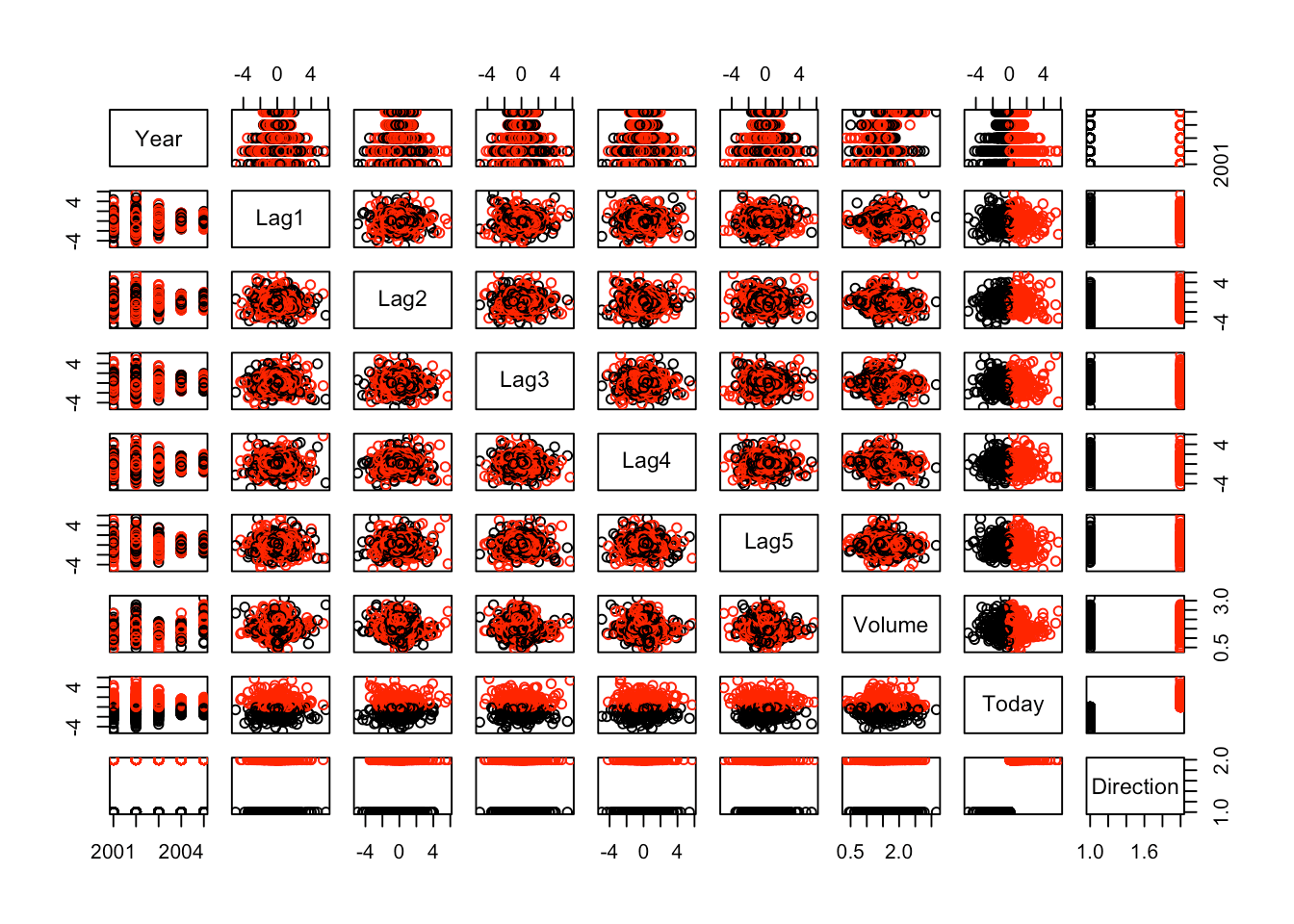
看起来这里没有太多的相关性。 class变量是从Today变量派生的, 因此Up和Down似乎要相除。除此之外, 没有太多事情发生。
让我们看一下按Direction值细分的每个变量的密度分布。像上面的散点图矩阵一样, 按方向绘制的密度图可以帮助查看上下分离。它还可以帮助你了解变量的”方向”值中的重叠部分。
library(caret)
x <- Smarket[, 1:8]
y <- Smarket[, 9]
scales <- list(x=list(relation="free"), y=list(relation="free"))
featurePlot(x=x, y=y, plot="density", scales=scales)
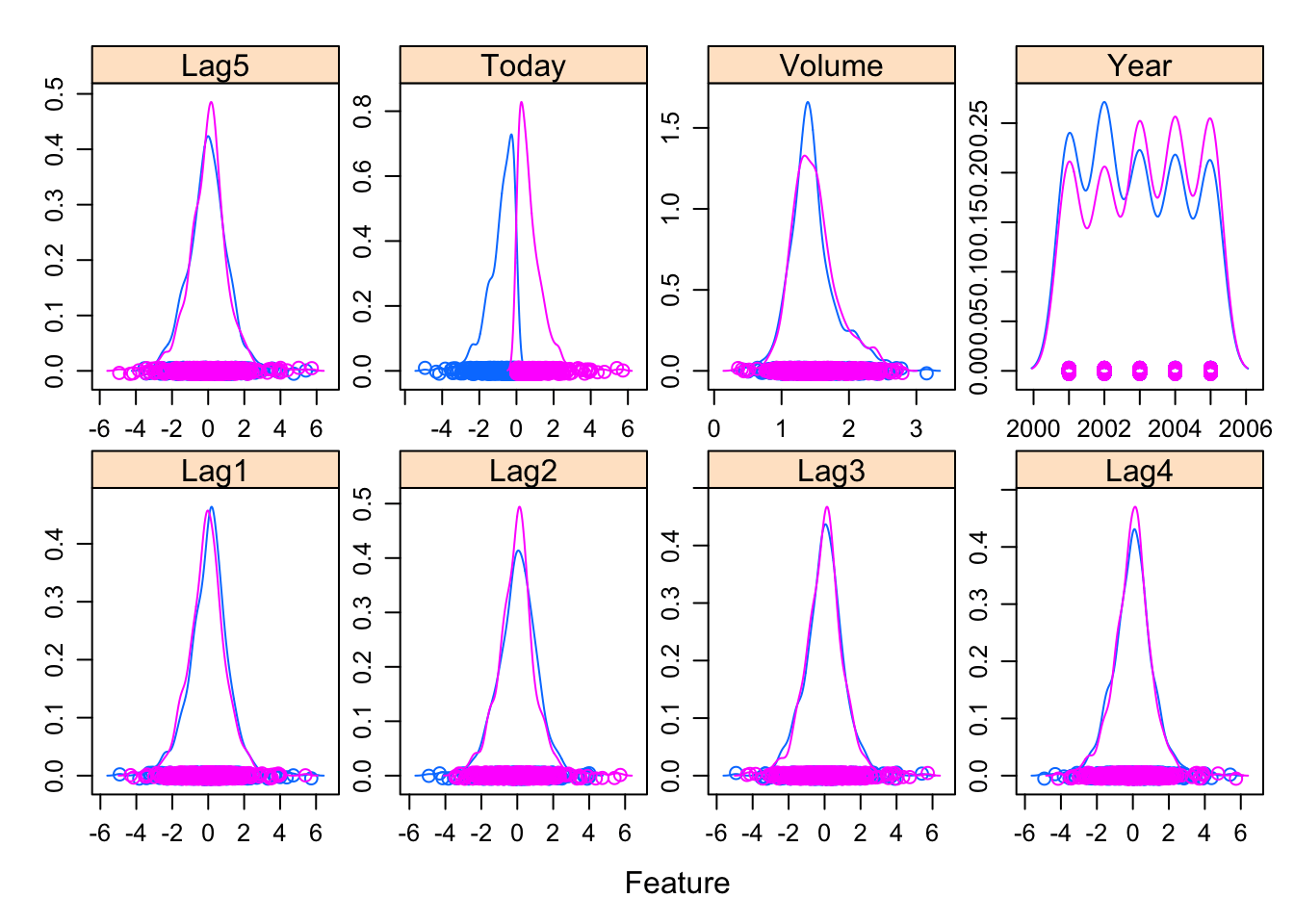
你会看到, 所有这些变量的Direction值都重叠, 这意味着很难仅根据一个或两个变量来预测Up或Down。
建立逻辑回归模型
现在调用glm.fit()函数。传递给此函数的第一个参数是R公式。在这种情况下, 该公式表示Direction是响应, 而Lag和Volume变量是预测变量。正如你在简介中所看到的, glm通常用于拟合广义线性模型。
但是, 在这种情况下, 你需要明确说明要拟合逻辑回归模型。你可以通过将family参数设置为二项式来解决此问题。这样, 你告诉glm()放置逻辑回归模型, 而不是其他可以拟合glm的模型之一。
# Logistics Regression
glm.fit <- glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume, data = Smarket, family = binomial)
接下来, 你可以执行summary(), 它告诉你有关拟合的一些信息:
summary(glm.fit)
##
## Call:
## glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
## Volume, family = binomial, data = Smarket)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.446 -1.203 1.065 1.145 1.326
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.126000 0.240736 -0.523 0.601
## Lag1 -0.073074 0.050167 -1.457 0.145
## Lag2 -0.042301 0.050086 -0.845 0.398
## Lag3 0.011085 0.049939 0.222 0.824
## Lag4 0.009359 0.049974 0.187 0.851
## Lag5 0.010313 0.049511 0.208 0.835
## Volume 0.135441 0.158360 0.855 0.392
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1731.2 on 1249 degrees of freedom
## Residual deviance: 1727.6 on 1243 degrees of freedom
## AIC: 1741.6
##
## Number of Fisher Scoring iterations: 3
如你所见, summary()返回每个系数的估计值, 标准误差, z得分和p值。看起来这里没有一个系数是重要的。它还为你提供零偏差(仅针对均值的偏差)和残余偏差(与所有预测变量的模型的偏差)。 2和6自由度之间的差异很小。
你将glm.fit()的predict()的结果分配给glm.probs, 其类型等于response。这将对你用于拟合模型的训练数据做出预测, 并为我提供拟合概率的向量。
你看一下前5个概率, 它们非常接近50%:
glm.probs <- predict(glm.fit, type = "response")
glm.probs[1:5]
## 1 2 3 4 5
## 0.5070841 0.4814679 0.4811388 0.5152224 0.5107812
现在, 我将基于滞后和其他预测因素来预测市场是上涨还是下跌。特别是, 我将阈值设为0.5将概率转化为分类。为此, 我使用了ifelse()命令。
glm.pred <- ifelse(glm.probs > 0.5, "Up", "Down")
glm.pred是对与错的向量。如果glm.probs大于0.5, 则glm.pred调用” Up”;否则, 调用” Up”。否则, 它称为” False”。
在这里, 你将数据框附加到Smarket并创建一个glm.pred表, 该表是前一个方向的起伏。你还可以取那些意思。
attach(Smarket)
table(glm.pred, Direction)
## Direction
## glm.pred Down Up
## Down 145 141
## Up 457 507
mean(glm.pred == Direction)
## [1] 0.5216
从表中, 对角线上的实例是你获得正确分类的地方, 而对角线上的实例则是你犯错的地方。看来你犯了很多错误。平均值的比例为0.52。
创建培训和测试样本
你如何做得更好?将数据分为训练集和测试集是一个很好的策略。
# Make training and test set
train = Year<2005
glm.fit <- glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume, data = Smarket, family = binomial, subset = train)
glm.probs <- predict(glm.fit, newdata = Smarket[!train, ], type = "response")
glm.pred <- ifelse(glm.probs > 0.5, "Up", "Down")
让我们详细看一下这段代码:
- 火车等于小于2005的年份。对于小于2005的所有年份, 你将得到一个真实的值。否则, 我会得到一个假的。
- 然后, 你使用glm.fit()重新拟合模型, 除了子集等于’train’, 这意味着它仅适合小于2005年的数据。
- 然后, 对glm.probs再次使用predict()函数, 以预测大于或等于2005年的剩余数据。对于新数据, 将其赋予Smarket, 由!train索引(如果年份为大于或等于2005)。你将类型设置为”响应”以预测概率。
- 最后, 对glm.pred再次使用ifelse()函数来制作Up和Down变量。
现在, 你将创建一个新变量来存储测试数据的新子集, 并将其命名为Direction.2005。响应变量仍然是Direction。你制作一张表格并计算此新测试集的均值:
Direction.2005 = Smarket$Direction[!train]
table(glm.pred, Direction.2005)
## Direction.2005
## glm.pred Down Up
## Down 77 97
## Up 34 44
mean(glm.pred == Direction.2005)
## [1] 0.4801587
哈, 你的情况比以前的情况差。怎么会这样
解决过度拟合
好吧, 你可能已经过度拟合了数据。为了解决这个问题, 你将要拟合一个较小的模型, 并使用Lag1, Lag2, Lag3作为预测变量, 从而省略所有其他变量。其余代码相同。
# Fit a smaller model
glm.fit = glm(Direction ~ Lag1 + Lag2 + Lag3, data = Smarket, family = binomial, subset = train)
glm.probs = predict(glm.fit, newdata = Smarket[!train, ], type = "response")
glm.pred = ifelse(glm.probs > 0.5, "Up", "Down")
table(glm.pred, Direction.2005)
## Direction.2005
## glm.pred Down Up
## Down 39 31
## Up 72 110
mean(glm.pred == Direction.2005)
## [1] 0.5912698
好吧, 你的分类率为59%, 还不错。使用较小的模型似乎会更好。
最后, 你将对glm.fit做一个summary()来查看是否有任何重大变化。
summary(glm.fit)
##
## Call:
## glm(formula = Direction ~ Lag1 + Lag2 + Lag3, family = binomial, ## data = Smarket, subset = train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.338 -1.189 1.072 1.163 1.335
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.032230 0.063377 0.509 0.611
## Lag1 -0.055523 0.051709 -1.074 0.283
## Lag2 -0.044300 0.051674 -0.857 0.391
## Lag3 0.008815 0.051495 0.171 0.864
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1383.3 on 997 degrees of freedom
## Residual deviance: 1381.4 on 994 degrees of freedom
## AIC: 1389.4
##
## Number of Fisher Scoring iterations: 3
没有任何事情变得重要, 至少P值更好, 表明对性能的预测有所提高。
总结
这就是本R教程的结尾, 该教程使用glm()函数构建逻辑回归模型并将族设置为二项式。 glm()不假设因变量和自变量之间存在线性关系。但是, 它假设logit模型中链接函数和自变量之间存在线性关系, 我希望你学到了一些有价值的东西!
 srcmini
srcmini
评论前必须登录!
注册