在Keras中实现自动编码器：权威教程

本文概述

• 使用Keras在Python中进行卷积自动编码器
• 去噪自动编码器
• 去噪自动编码器的实现
• 走得更远！

通常, 你可以将自动编码器视为一种无监督的学习技术, 因为你不需要明确的标签来训练模型。训练自动编码器所需要做的就是输入原始数据。

在本教程中, 你将学习深度学习中的自动编码器, 并使用Keras在Python中实现卷积和去噪自动编码器。你将以NotMNIST字母数据集为例。

简而言之, 你将在本教程中解决以下主题：

• 你将首先了解有关自动编码器的更多信息：它们是什么, 它们与降维技术的比较方式, 以及该算法可以找到的不同类型；
• 接下来, 你将专注于卷积自动编码器：首先将了解这种类型的自动编码器的功能以及如何构造它。之后, 你将自己实施！你将学习如何以ubyte gzip格式加载数据, 然后探索数据, 预处理数据, 将数据拟合到模型中, 可视化训练和验证损失图并最终在测试集上进行预测。
• 接下来, 将向你介绍去噪自动编码器, 并了解如何实现该功能：你将学习为图像添加噪点。接下来, 你将把这些图像输入到你的深度学习模型中并进行训练！最后, 你将预测嘈杂的测试图像。

正如你在简介中所读到的, 自动编码器是一种无监督的机器学习算法, 该算法将图像作为输入, 并尝试使用来自瓶颈(也称为潜在空间)的较少位数来重建图像。图像主要在瓶颈处被压缩。通过对网络进行一段时间的训练, 可以实现自动编码器中的压缩, 并且在了解到这一点后, 它会尽力在瓶颈处最好地表示输入图像。诸如JPEG和JPEG无损压缩技术之类的常规图像压缩算法无需任何培训即可压缩图像, 并且在压缩图像方面做得相当好。

自动编码器类似于降维技术, 例如主成分分析(PCA)。他们使用线性变换将数据从较高维度投影到较低维度, 并尝试在删除非必要部分的同时保留数据的重要特征。

但是, 自动编码器和PCA之间的主要区别在于转换部分：正如你已经阅读的, PCA使用线性转换, 而自动编码器使用非线性转换。

现在你对自动编码器有了一些了解, 现在让我们打破这个术语, 并尝试获得一些直觉吧！

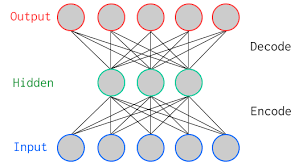
上图是两层香草自动编码器, 其中有一个隐藏层。在深度学习术语中, 你经常会注意到, 在计算架构中的层总数时, 永远不会考虑输入层。体系结构中的总层仅包含隐藏层和输出层的数量。

如上图所示, 输入层和输出层具有相同数量的神经元。

让我们举个例子。你将仅具有五个像素值的图像馈入自动编码器, 该图像由编码器在瓶颈(中间层)或潜在空间处压缩为三个像素值。使用这三个值, 解码器将尝试重建五个像素值, 或更确切地说是你作为输入输入到网络的输入图像。

实际上, 输入和输出之间存在更多的隐藏层。

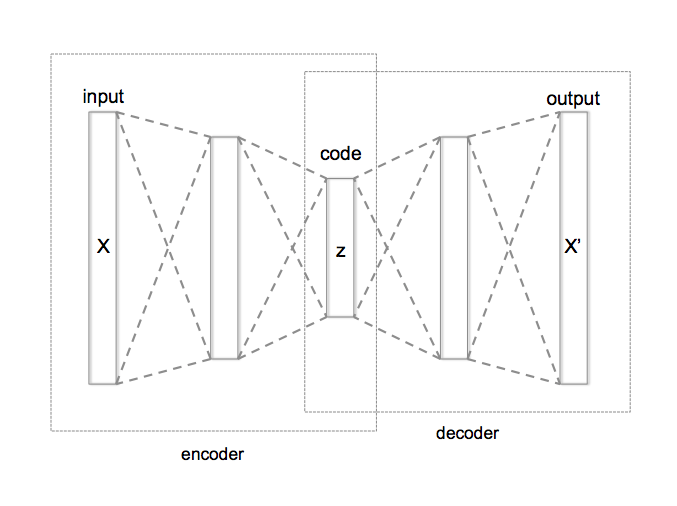
自动编码器可以分为三个部分

• 编码器：网络的这一部分将输入压缩或下采样为更少的位数。这些较少数目的位所表示的空间通常称为潜在空间或瓶颈。瓶颈也称为”最大压缩点”, 因为在此点输入被最大压缩。这些代表原始输入的压缩位统称为输入的”编码”。
• 解码器：网络的这一部分尝试仅使用输入的编码来重建输入。当解码器能够完全按照输入给编码器的方式重构输入时, 可以说编码器能够为输入产生最佳的编码, 从而解码器能够很好地重构！

有多种自动编码器, 例如卷积自动编码器, 降噪自动编码器, 变分自动编码器和稀疏自动编码器。但是, 正如你在简介中所阅读的那样, 在本教程中, 你将只关注卷积和去噪。

使用Keras在Python中进行卷积自动编码器

由于输入数据包含图像, 因此最好使用卷积自动编码器。它不是自动编码器的变体, 而是堆叠有卷积层的传统自动编码器：你基本上用卷积层代替了完全连接的层。卷积层与最大池化层一起将输入(从宽(28 x 28图像)和薄(单通道或灰度)转换为小(在潜在空间为7 x 7图像)和厚(128通道)。

如果你没有正确理解上述想法, 请不要担心！本教程的第二部分将重点介绍上述内容的实现, 希望可以消除所有疑问(如果有任何疑问！)。

提示：如果你想进一步了解卷积神经网络, 请查看本教程。

这有助于网络从图像中提取视觉特征, 从而获得更准确的潜在空间表示。重构过程使用上采样和卷积, 这被称为解码器。下采样是将图像压缩为低尺寸(也称为编码器)的过程。

请务必注意, 编码器主要压缩输入图像, 例如：如果输入图像的尺寸为176 x 176 x 1(〜30976), 则最大压缩点的尺寸可以为22 x 22 x 512( 〜247808)。因此, 在这种情况下, 你首先使用尺寸为176 x 176的灰度图像, 然后将其通过几个卷积层以及恰好是三个最大池化层, 最后将图像降采样为22 x 22的尺寸, 但是通道数从1增加到512。如上所述, 宽(176 x 176)和薄(1)的输入变小(22×22)和厚(512)。

加载数据

notMNIST数据集是从字母A到J的字体glypyhs的图像识别数据集。它与经典MNIST数据集非常相似, 后者包含手写数字0到9的图像：在这种情况下, 你会发现NotMNIST数据集包含28×28灰度图像, 其中A-J共70个字母, 共10个类别, 每个类别6, 000个图像。

提示：如果你想学习如何使用MNIST数据集为分类任务实现多层感知器(MLP), 请查看本教程。

在Keras或TensorFlow框架中未预定义NotMNIST数据集, 因此你必须从此源下载数据。数据将以ubyte.gzip格式下载, 但现在无需担心！你将很快学习如何读取字节流格式并将其转换为NumPy数组。所以, 让我们开始吧！

该网络将在Nvidia Tesla K40上进行训练, 因此, 如果在GPU上进行训练并使用Jupyter Notebook, 则需要再添加三行代码, 在其中使用称为os的模块指定CUDA设备顺序和CUDA可见设备。

在下面的代码中, 你基本上使用os.environ在笔记本中设置了环境变量。在初始化Keras以限制Keras后端TensorFlow使用第一个GPU之前, 最好执行以下操作。如果你要在其上训练的机器的GPU为0, 请确保使用0而不是1。你可以通过在终端上运行一个简单的命令来进行检查：例如nvidia-smi

import os
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"]="1" #model will be trained on GPU 1

接下来, 导入所有必需的模块, 例如numpy, matplotlib和最重要的是keras, 因为你将在今天的教程中使用该框架！

import keras
from matplotlib import pyplot as plt
import numpy as np
import gzip
%matplotlib inline
from keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras.optimizers import RMSprop

Using TensorFlow backend.

在这里, 你定义了一个打开gzip文件, 使用bytestream.read()读取文件的函数。你将图像尺寸和图像总数传递给此功能。然后, 使用np.frombuffer()将存储在变量buf中的字符串转换为float32类型的NumPy数组。

接下来, 将数组重塑为三维数组或张量, 其中第一维是图像数, 第二维和第三维是图像的维数。最后, 返回NumPy数组数据。

def extract_data(filename, num_images):
    with gzip.open(filename) as bytestream:
        bytestream.read(16)
        buf = bytestream.read(28 * 28 * num_images)
        data = np.frombuffer(buf, dtype=np.uint8).astype(np.float32)
        data = data.reshape(num_images, 28, 28)
        return data

现在, 你将传递训练和测试文件以及相应的图像数量, 以调用函数extract_data()：

train_data = extract_data('train-images-idx3-ubyte.gz', 60000)
test_data = extract_data('t10k-images-idx3-ubyte.gz', 10000)

同样, 你定义了一个提取标签功能, 该功能可打开gzip文件, 并使用bytestream.read()读取文件, 并向其传递标签尺寸(1)和图像总数。然后, 使用np.frombuffer()将存储在变量buf中的字符串转换为int64类型的NumPy数组。

这次, 你不需要重新调整数组的形状, 因为变量标签将返回尺寸为60, 000 x 1的列向量。最后, 你将返回NumPy数组标签。

def extract_labels(filename, num_images):
    with gzip.open(filename) as bytestream:
        bytestream.read(8)
        buf = bytestream.read(1 * num_images)
        labels = np.frombuffer(buf, dtype=np.uint8).astype(np.int64)
        return labels

现在, 你将通过传递训练和测试标签文件及其相应的图像数量来调用函数提取标签：

train_labels = extract_labels('train-labels-idx1-ubyte.gz', 60000)
test_labels = extract_labels('t10k-labels-idx1-ubyte.gz', 10000)

一旦加载了训练和测试数据, 就可以对数据进行全部分析, 以获取有关本教程要使用的数据集的直观信息！

数据探索

现在让我们分析数据集中的图像外观, 并借助NumPy数组属性.shape来查看图像的尺寸：

# Shapes of training set
print("Training set (images) shape: {shape}".format(shape=train_data.shape))

# Shapes of test set
print("Test set (images) shape: {shape}".format(shape=test_data.shape))

Training set (images) shape: (60000, 28, 28)
Test set (images) shape: (10000, 28, 28)

从上面的输出中, 你可以看到训练数据的形状为60000 x 28 x 28, 因为每个28 x 28维矩阵都有60, 000个训练样本。同样, 由于有10, 000个测试样本, 因此测试数据的形状为10000 x 28 x 28。

请注意, 在此任务中, 你将不会使用培训和测试标签。手头的任务将只是处理训练和测试图像。但是, 出于探索目的, 这可能会使你对数据有更好的直觉, 你将使用标签。

让我们创建一个字典, 该字典将具有带有相应类别分类标签的类名：

# Create dictionary of target classes
label_dict = {
 0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F', 6: 'G', 7: 'H', 8: 'I', 9: 'J', }

现在, 让我们看一下数据集中的几个图像：

plt.figure(figsize=[5, 5])

# Display the first image in training data
plt.subplot(121)
curr_img = np.reshape(train_data[0], (28, 28))
curr_lbl = train_labels[0]
plt.imshow(curr_img, cmap='gray')
plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")

# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(test_data[0], (28, 28))
curr_lbl = test_labels[0]
plt.imshow(curr_img, cmap='gray')
plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")

<matplotlib.text.Text at 0x7f3ec73db240>

上面两个图的输出是来自训练和测试数据的样本图像之一, 这些图像一方面被分配为5或F, 另一方面被分配为3或D的类别标签。同样, 其他字母将具有不同的标签, 但相似的字母将具有相同的标签。这意味着所有6, 000张F类图像将具有5级标签。

数据预处理

数据集的图像确实是灰度图像, 像素值为0到255, 尺寸为28 x 28, 因此在将数据输入模型之前, 对其进行预处理非常重要。首先, 将火车和测试集的每个28 x 28图像转换为大小为28 x 28 x 1的矩阵, 你可以将其输入网络：

train_data = train_data.reshape(-1, 28, 28, 1)
test_data = test_data.reshape(-1, 28, 28, 1)
train_data.shape, test_data.shape

((60000, 28, 28, 1), (10000, 28, 28, 1))

接下来, 你要确保检查训练和测试NumPy数组的数据类型, 该数据类型应为float32格式, 如果不是, 则需要将其转换为该格式, 但是由于在读取数据时已经对其进行了转换你不再需要再次执行此操作。你还必须在0-1(含)范围内重新缩放像素值。因此, 让我们开始吧！

不要忘记验证培训和测试数据类型：

train_data.dtype, test_data.dtype

(dtype('float32'), dtype('float32'))

接下来, 使用训练和测试数据的最大像素值重新缩放训练和测试数据：

np.max(train_data), np.max(test_data)

(255.0, 255.0)

train_data = train_data / np.max(train_data)
test_data = test_data / np.max(test_data)

重新缩放后, 让我们验证训练和测试数据的最大值, 该值为1.0！

np.max(train_data), np.max(test_data)

(1.0, 1.0)

完成所有这些之后, 对数据进行分区很重要。为了使模型更好地泛化, 你将训练数据分为两部分：训练和验证集。你将在80％的数据上训练模型, 并在剩余训练数据的20％上验证模型。

这也将帮助你减少过度拟合的机会, 因为你将根据训练阶段无法看到的数据来验证模型。

你可以使用scikit-learn的train_test_split模块正确地划分数据：

from sklearn.model_selection import train_test_split
train_X, valid_X, train_ground, valid_ground = train_test_split(train_data, train_data, test_size=0.2, random_state=13)

请注意, 对于此任务, 你不需要培训和测试标签。这就是为什么你将两次通过训练图像。与分类任务中的标签类似, 你的训练图像将既是输入也是基础事实。

现在你已经准备好定义网络并将数据馈入网络。因此, 事不宜迟, 让我们跳到下一步！

卷积自动编码器

图像的尺寸为28 x 28 x 1或784维矢量。你将图像矩阵转换为数组, 在0到1之间重新缩放, 重新调整形状使其大小为28 x 28 x 1, 并将其作为输入馈送到网络。

同样, 你将使用128的批次大小, 最好使用256或512的较高批次大小, 这完全取决于你训练模型的系统。它在确定学习参数方面做出了巨大贡献, 并影响了预测准确性。你将训练你的网络50个纪元。

batch_size = 128
epochs = 50
inChannel = 1
x, y = 28, 28
input_img = Input(shape = (x, y, inChannel))

如前所述, 自动编码器分为两个部分：有一个编码器和一个解码器。

编码器

• 第一层将包含32个大小为3 x 3的滤镜, 然后是下采样(最大合并)层,
• 第二层将包含64个尺寸为3 x 3的滤镜, 然后是另一个下采样层,
• 编码器的最后一层将具有大小为3 x 3的128个滤波器。

解码器

• 第一层将具有大小为3 x 3的128个滤镜, 然后是上采样层, / li>
• 第二层将包含64个尺寸为3 x 3的滤镜, 然后是另一个上采样层,
• 编码器的最后一层将具有1个大小为3 x 3的滤波器。

每次使用时, 最大池化层将对输入进行两次下采样, 而每次使用时, 向上采样层将对输入进行两次下采样。

注意：滤波器的数量, 滤波器的大小, 层数, 训练模型的时期数都是超参数, 应根据自己的直觉来决定, 你可以通过调整这些超参数和衡量模型的性能。这就是你将如何慢慢学习深度学习的艺术！

def autoencoder(input_img):
    #encoder
    #input = 28 x 28 x 1 (wide and thin)
    conv1 = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img) #28 x 28 x 32
    pool1 = MaxPooling2D(pool_size=(2, 2))(conv1) #14 x 14 x 32
    conv2 = Conv2D(64, (3, 3), activation='relu', padding='same')(pool1) #14 x 14 x 64
    pool2 = MaxPooling2D(pool_size=(2, 2))(conv2) #7 x 7 x 64
    conv3 = Conv2D(128, (3, 3), activation='relu', padding='same')(pool2) #7 x 7 x 128 (small and thick)

    #decoder
    conv4 = Conv2D(128, (3, 3), activation='relu', padding='same')(conv3) #7 x 7 x 128
    up1 = UpSampling2D((2, 2))(conv4) # 14 x 14 x 128
    conv5 = Conv2D(64, (3, 3), activation='relu', padding='same')(up1) # 14 x 14 x 64
    up2 = UpSampling2D((2, 2))(conv5) # 28 x 28 x 64
    decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up2) # 28 x 28 x 1
    return decoded

创建模型后, 必须使用优化器将其编译为RMSProp。

提示：如果想进一步了解RMSProp, 请观看Andrew Ng在RMSProp上的本教程。

注意, 你还必须通过参数loss指定损失类型。在这种情况下, 这就是均方误差, 因为将使用逐像素均方误差来计算每批预测输出与地面实况之间的每批损失。

autoencoder = Model(input_img, autoencoder(input_img))
autoencoder.compile(loss='mean_squared_error', optimizer = RMSprop())

让我们使用摘要功能来可视化在上一步中创建的图层, 这将显示每个图层中的参数数量(权重和偏差)以及模型中的总参数。

autoencoder.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_6 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_25 (Conv2D)           (None, 28, 28, 32)        320       
_________________________________________________________________
max_pooling2d_9 (MaxPooling2 (None, 14, 14, 32)        0         
_________________________________________________________________
conv2d_26 (Conv2D)           (None, 14, 14, 64)        18496     
_________________________________________________________________
max_pooling2d_10 (MaxPooling (None, 7, 7, 64)          0         
_________________________________________________________________
conv2d_27 (Conv2D)           (None, 7, 7, 128)         73856     
_________________________________________________________________
conv2d_28 (Conv2D)           (None, 7, 7, 128)         147584    
_________________________________________________________________
up_sampling2d_9 (UpSampling2 (None, 14, 14, 128)       0         
_________________________________________________________________
conv2d_29 (Conv2D)           (None, 14, 14, 64)        73792     
_________________________________________________________________
up_sampling2d_10 (UpSampling (None, 28, 28, 64)        0         
_________________________________________________________________
conv2d_30 (Conv2D)           (None, 28, 28, 1)         577       
=================================================================
Total params: 314, 625
Trainable params: 314, 625
Non-trainable params: 0
_________________________________________________________________

终于是时候用Keras的fit()函数训练模型了！该模型训练了50个纪元。 fit()函数将返回一个历史对象；通过在fashion_train中讲述该函数的结果, 你以后可以使用它在训练和验证之间绘制损失函数图, 这将帮助你直观地分析模型的性能。

训练模型

autoencoder_train = autoencoder.fit(train_X, train_ground, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(valid_X, valid_ground))

Train on 48000 samples, validate on 12000 samples
Epoch 1/50
48000/48000 [==============================] - 16s - loss: 0.0368 - val_loss: 0.0132
Epoch 2/50
48000/48000 [==============================] - 15s - loss: 0.0101 - val_loss: 0.0085
Epoch 3/50
48000/48000 [==============================] - 15s - loss: 0.0071 - val_loss: 0.0081
Epoch 4/50
48000/48000 [==============================] - 15s - loss: 0.0057 - val_loss: 0.0056
Epoch 5/50
48000/48000 [==============================] - 15s - loss: 0.0048 - val_loss: 0.0051
Epoch 6/50
48000/48000 [==============================] - 15s - loss: 0.0043 - val_loss: 0.0039
Epoch 7/50
48000/48000 [==============================] - 15s - loss: 0.0038 - val_loss: 0.0039
Epoch 8/50
48000/48000 [==============================] - 15s - loss: 0.0035 - val_loss: 0.0039
Epoch 9/50
48000/48000 [==============================] - 15s - loss: 0.0032 - val_loss: 0.0030
Epoch 10/50
48000/48000 [==============================] - 15s - loss: 0.0030 - val_loss: 0.0029
Epoch 11/50
48000/48000 [==============================] - 15s - loss: 0.0029 - val_loss: 0.0026
Epoch 12/50
48000/48000 [==============================] - 15s - loss: 0.0027 - val_loss: 0.0025
Epoch 13/50
48000/48000 [==============================] - 15s - loss: 0.0026 - val_loss: 0.0028
Epoch 14/50
48000/48000 [==============================] - 15s - loss: 0.0025 - val_loss: 0.0022
Epoch 15/50
48000/48000 [==============================] - 15s - loss: 0.0024 - val_loss: 0.0024
Epoch 16/50
48000/48000 [==============================] - 16s - loss: 0.0023 - val_loss: 0.0027
Epoch 17/50
48000/48000 [==============================] - 15s - loss: 0.0023 - val_loss: 0.0022
Epoch 18/50
48000/48000 [==============================] - 16s - loss: 0.0022 - val_loss: 0.0025
Epoch 19/50
48000/48000 [==============================] - 16s - loss: 0.0022 - val_loss: 0.0022
Epoch 20/50
48000/48000 [==============================] - 15s - loss: 0.0021 - val_loss: 0.0022
Epoch 21/50
48000/48000 [==============================] - 16s - loss: 0.0021 - val_loss: 0.0020
Epoch 22/50
48000/48000 [==============================] - 16s - loss: 0.0020 - val_loss: 0.0019
Epoch 23/50
48000/48000 [==============================] - 16s - loss: 0.0020 - val_loss: 0.0021
Epoch 24/50
48000/48000 [==============================] - 16s - loss: 0.0020 - val_loss: 0.0018
Epoch 25/50
48000/48000 [==============================] - 16s - loss: 0.0019 - val_loss: 0.0020
Epoch 26/50
48000/48000 [==============================] - 16s - loss: 0.0019 - val_loss: 0.0020
Epoch 27/50
48000/48000 [==============================] - 16s - loss: 0.0019 - val_loss: 0.0017
Epoch 28/50
48000/48000 [==============================] - 16s - loss: 0.0018 - val_loss: 0.0018
Epoch 29/50
48000/48000 [==============================] - 16s - loss: 0.0018 - val_loss: 0.0019
Epoch 30/50
48000/48000 [==============================] - 16s - loss: 0.0018 - val_loss: 0.0017
Epoch 31/50
48000/48000 [==============================] - 16s - loss: 0.0018 - val_loss: 0.0019
Epoch 32/50
48000/48000 [==============================] - 16s - loss: 0.0017 - val_loss: 0.0018
Epoch 33/50
48000/48000 [==============================] - 16s - loss: 0.0017 - val_loss: 0.0017
Epoch 34/50
48000/48000 [==============================] - 15s - loss: 0.0017 - val_loss: 0.0018
Epoch 35/50
48000/48000 [==============================] - 15s - loss: 0.0017 - val_loss: 0.0019
Epoch 36/50
48000/48000 [==============================] - 15s - loss: 0.0017 - val_loss: 0.0016
Epoch 37/50
48000/48000 [==============================] - 15s - loss: 0.0017 - val_loss: 0.0017
Epoch 38/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0019
Epoch 39/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0015
Epoch 40/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0017
Epoch 41/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0017
Epoch 42/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0014
Epoch 43/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0018
Epoch 44/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0015
Epoch 45/50
48000/48000 [==============================] - 15s - loss: 0.0016 - val_loss: 0.0014
Epoch 46/50
48000/48000 [==============================] - 16s - loss: 0.0015 - val_loss: 0.0016
Epoch 47/50
48000/48000 [==============================] - 16s - loss: 0.0015 - val_loss: 0.0017
Epoch 48/50
48000/48000 [==============================] - 16s - loss: 0.0015 - val_loss: 0.0015
Epoch 49/50
48000/48000 [==============================] - 16s - loss: 0.0015 - val_loss: 0.0016
Epoch 50/50
48000/48000 [==============================] - 16s - loss: 0.0015 - val_loss: 0.0020

最后！你在Not-MNIST上对模型进行了50个训练, 现在, 让我们在训练和验证数据之间绘制损失图, 以可视化模型的性能。

培训与验证损失图

loss = autoencoder_train.history['loss']
val_loss = autoencoder_train.history['val_loss']
epochs = range(epochs)
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()

最后, 你可以看到验证损失和训练损失都是同步的。它表明你的模型不是过拟合的：验证损失正在减少而不是增加, 并且训练和验证损失之间几乎没有任何差距。

因此, 可以说模型的泛化能力很好。

最后, 是时候使用Keras的predict()函数重建测试图像了, 看看你的模型在测试数据上的重建能力如何。

预测测试数据

你将在完整的10, 000个测试图像上预测经过训练的模型, 并绘制少量重构图像以可视化模型重构测试图像的能力。

pred = autoencoder.predict(test_data)

pred.shape

(10000, 28, 28, 1)

plt.figure(figsize=(20, 4))
print("Test Images")
for i in range(10):
    plt.subplot(2, 10, i+1)
    plt.imshow(test_data[i, ..., 0], cmap='gray')
    curr_lbl = test_labels[i]
    plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")
plt.show()    
plt.figure(figsize=(20, 4))
print("Reconstruction of Test Images")
for i in range(10):
    plt.subplot(2, 10, i+1)
    plt.imshow(pred[i, ..., 0], cmap='gray')  
plt.show()

Test Images

Reconstruction of Test Images

从上图可以看出, 你的模型在重建使用该模型预测的测试图像方面做得非常出色。至少在视觉上, 测试和重建的图像看起来几乎完全相似。

去噪自动编码器

去噪自动编码器尝试学习对噪声具有鲁棒性的表示形式(潜在空间或瓶颈)。你向图像添加了噪点, 然后将嘈杂的图像作为输入输入到网络的增强器部分。自动编码器的编码器部分将图像转换为一个不同的空间, 该空间试图保留字母但消除噪声。

但是如何准确消除噪音呢？

在训练期间, 你定义一个损失函数, 类似于你先前在卷积自动编码器中定义的均方根误差。在训练的每次迭代中, 网络都会计算解码器输出的噪点图像与地面真实情况(噪点图像)之间的损失, 并且还将尝试最小化重建图像与原始无噪声图像之间的损失或差异。换句话说, 网络将学习7 x 7 x 128的空间, 该空间将是训练网络所用数据的无噪声编码！

去噪自动编码器的实现

现在, 要了解它在Python中的工作方式, 你将使用与本教程第一部分相同的NotMNIST数据集。这意味着你不需要进行任何数据预处理, 因为它已经完成了！但是, 本教程此部分中的一个重要的预处理步骤将为训练, 验证和测试图像增加噪音。因此, 让我们先快速进行操作！

给图像添加噪点

首先定义一个噪声参数, 它是一个超参数。噪声因子乘以平均值为0.0, 标准差为1.0的随机矩阵。该矩阵将从正态(高斯)分布中抽取样本。随机法线阵列的形状类似于你将添加噪声的数据的形状。

为简单起见, 让我们以一个示例来理解它：变量train_X的形状为48000 x 28 x 28 x1。因此, 随机法线数组也将具有与train_X相似的形状, 只有这样你才能添加两个数组, 因为那么它们将具有相同的尺寸。

noise_factor = 0.5
x_train_noisy = train_X + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_X.shape)
x_valid_noisy = valid_X + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=valid_X.shape)
x_test_noisy = test_data + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=test_data.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_valid_noisy = np.clip(x_valid_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)

np.clip()会将所有负值的阈值设置为零, 并且所有大于1的值都设置为阈值。既然如此, 你希望像素值介于零和一之间。而且, 在将噪声引入数据后, 像素值范围可能会有所变化, 因此, 为了安全起见, 最好修剪一下像素值。

可视化嘈杂的图像

plt.figure(figsize=[5, 5])

# Display the first image in training data
plt.subplot(121)
curr_img = np.reshape(x_train_noisy[1], (28, 28))
plt.imshow(curr_img, cmap='gray')

# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(x_test_noisy[1], (28, 28))
plt.imshow(curr_img, cmap='gray')

<matplotlib.image.AxesImage at 0x7f3ec6b20e48>

有了嘈杂的数据之后, 你就可以将其输入网络了, 看看如何从图像中”神奇地”消除噪音！

去噪自动编码器网络

如前所述, 自动编码器分为两个部分：编码器和解码器。你将要构建的架构如下所示：

编码器

• 第一层将包含32-3 x 3个滤镜, 然后是下采样(最大合并)层,
• 第二层将具有64-3 x 3滤镜, 然后是另一个下采样层,
• 编码器的最后一层将具有128-3 x 3滤镜。

解码器

• 第一层将具有128-3 x 3滤镜, 其后是一个上采样层,
• 第二层将具有64-3 x 3滤镜, 然后是另一个上采样层,
• 编码器的最后一层将具有1-3 x 3滤镜。

batch_size = 128
epochs = 20
inChannel = 1
x, y = 28, 28
input_img = Input(shape = (x, y, inChannel))

def autoencoder(input_img):
    #encoder
    conv1 = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
    pool1 = MaxPooling2D(pool_size=(2, 2))(conv1)
    conv2 = Conv2D(64, (3, 3), activation='relu', padding='same')(pool1)
    pool2 = MaxPooling2D(pool_size=(2, 2))(conv2)
    conv3 = Conv2D(128, (3, 3), activation='relu', padding='same')(pool2)

    #decoder
    conv4 = Conv2D(128, (3, 3), activation='relu', padding='same')(conv3)
    up1 = UpSampling2D((2, 2))(conv4)
    conv5 = Conv2D(64, (3, 3), activation='relu', padding='same')(up1)
    up2 = UpSampling2D((2, 2))(conv5)
    decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up2)
    return decoded

autoencoder = Model(input_img, autoencoder(input_img))
autoencoder.compile(loss='mean_squared_error', optimizer = RMSprop())

训练

如果你记得在训练卷积自动编码器时, 由于输入和地面真相都是相同的, 那么你已经输入了两次训练图像。但是, 在对自动编码器进行降噪时, 你会将有噪声的图像作为输入, 而你的地面真实情况仍然是施加了噪声的噪声图像。只有这样, 网络才能够计算噪声图像和真实噪声图像之间的损耗。

autoencoder_train = autoencoder.fit(x_train_noisy, train_X, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_valid_noisy, valid_X))

Train on 48000 samples, validate on 12000 samples
Epoch 1/20
48000/48000 [==============================] - 15s - loss: 0.0531 - val_loss: 0.0268
Epoch 2/20
48000/48000 [==============================] - 14s - loss: 0.0243 - val_loss: 0.0217
Epoch 3/20
48000/48000 [==============================] - 14s - loss: 0.0207 - val_loss: 0.0200
Epoch 4/20
48000/48000 [==============================] - 14s - loss: 0.0190 - val_loss: 0.0184
Epoch 5/20
48000/48000 [==============================] - 14s - loss: 0.0179 - val_loss: 0.0183
Epoch 6/20
48000/48000 [==============================] - 14s - loss: 0.0171 - val_loss: 0.0178
Epoch 7/20
48000/48000 [==============================] - 14s - loss: 0.0165 - val_loss: 0.0161
Epoch 8/20
48000/48000 [==============================] - 14s - loss: 0.0160 - val_loss: 0.0166
Epoch 9/20
48000/48000 [==============================] - 14s - loss: 0.0157 - val_loss: 0.0157
Epoch 10/20
48000/48000 [==============================] - 14s - loss: 0.0153 - val_loss: 0.0159
Epoch 11/20
48000/48000 [==============================] - 14s - loss: 0.0151 - val_loss: 0.0153
Epoch 12/20
48000/48000 [==============================] - 14s - loss: 0.0148 - val_loss: 0.0154
Epoch 13/20
48000/48000 [==============================] - 14s - loss: 0.0146 - val_loss: 0.0151
Epoch 14/20
48000/48000 [==============================] - 14s - loss: 0.0145 - val_loss: 0.0152
Epoch 15/20
48000/48000 [==============================] - 14s - loss: 0.0143 - val_loss: 0.0163
Epoch 16/20
48000/48000 [==============================] - 14s - loss: 0.0141 - val_loss: 0.0152
Epoch 17/20
48000/48000 [==============================] - 14s - loss: 0.0140 - val_loss: 0.0149
Epoch 18/20
48000/48000 [==============================] - 14s - loss: 0.0139 - val_loss: 0.0153
Epoch 19/20
48000/48000 [==============================] - 14s - loss: 0.0138 - val_loss: 0.0152
Epoch 20/20
48000/48000 [==============================] - 14s - loss: 0.0137 - val_loss: 0.0150

训练与验证损失图

loss = autoencoder_train.history['loss']
val_loss = autoencoder_train.history['val_loss']
epochs = range(epochs)
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()

从上面的图表中, 你可以得出一些直觉, 即模型在大多数时期都处于过度拟合状态, 而在大多数情况下仍处于同步状态。你肯定可以通过引入一些复杂性来尝试提高模型的性能, 以使损失可以减少更多, 尝试训练更多的时期然后做出决定。

根据测试数据集预测

pred = autoencoder.predict(x_test_noisy)

plt.figure(figsize=(20, 4))
print("Test Images")
for i in range(10, 20, 1):
    plt.subplot(2, 10, i+1)
    plt.imshow(test_data[i, ..., 0], cmap='gray')
    curr_lbl = test_labels[i]
    plt.title("(Label: " + str(label_dict[curr_lbl]) + ")")
plt.show()    
plt.figure(figsize=(20, 4))
print("Test Images with Noise")
for i in range(10, 20, 1):
    plt.subplot(2, 10, i+1)
    plt.imshow(x_test_noisy[i, ..., 0], cmap='gray')
plt.show()    

plt.figure(figsize=(20, 4))
print("Reconstruction of Noisy Test Images")
for i in range(10, 20, 1):
    plt.subplot(2, 10, i+1)
    plt.imshow(pred[i, ..., 0], cmap='gray')  
plt.show()

Test Images

Test Images with Noise

Reconstruction of Noisy Test Images

看起来, 在短短20个周期内, 一个相当简单的网络体系结构在消除测试图像中的噪声方面做得很好, 不是吗？

走得更远！

本教程是从理论上和实践上理解自动编码器的良好起点。如果你能够轻松地进行工作, 甚至只需付出更多的努力, 那就做好了！

在下一个教程中, 你将学习如何从头开始读取图像, 进行分析, 预处理并使用指纹数据集将其输入模型。你还将学习如何读取T-1模态的医学图像并使用自动编码器对其进行重建！

还有很多内容要讲, 为什么不参加srcmini的Python深度学习课程呢？如果你还没有这样做的话。你将从基础知识中学习, 然后慢慢进入精通深度学习领域, 当你学习如何在Python中使用卷积神经网络, 如何检测面部, 物体等时, 毫无疑问它将是必不可少的资源。