本文概述
我们最近启动了一个名为DataFramed的新数据科学播客, 我在其中与来自学术界和行业的专家和思想领袖进行了交谈, 探讨了数据科学在实践中的样子以及它如何改变社会。我经常问客人, 他们的数据科学技术是什么。
本教程是我们一周前完成的Facebook Live活动的一部分, 它将带你逐步学习其中的内容!
在本教程中, 你将了解
- 散点图
- 决策树
- 线性回归
- 使用对数轴
- 逻辑回归
- 主成分分析(PCA)
你可以在iTunes以及Google Play商店中订阅DataFramed。
送
我们也为那些为我们撰写iTunes评论的人提供礼物!随机抽取5位幸运的评论者将获得srcmini赃物:我们有运动衫, 钢笔, 贴纸, 你可以自己命名, 其中5位中的一位将被选为我们的播客细分之一来采访我!
你需要做什么?
- 在iTunes商店中撰写DataFramed的评论
- 电子邮件dataframed@srcmini02.com的评论屏幕快照以及你在其中发布评论的国家/地区(请注意:除此赠品外, 不会定期检查此电子邮件地址)。
- 请在你所在时区的EOD 3月9日(星期五)之前完成这些操作。
散点图
Roger Peng出现在上周的DataFramed中。罗杰(Roger)是约翰霍普金斯大学彭博公共卫生学院生物统计学系的教授, 约翰霍普金斯大学数据科学实验室的联合主任和约翰霍普金斯大学数据科学专业的联合创始人。罗杰(Roger)还是经验丰富的播客, 播客不是标准差和工作量报告。在本集中, 我们讨论了数据科学, 它在研究环境和空气污染中的作用, 用于使数据科学民主化的大规模在线公开课程等等。
用罗杰的话说,
坦白说, 我最喜欢的工具只是一个散点图。我认为情节是如此的生动。坦率地说, 这并不是我看到的很多事情。我想原因, 我想为什么会这样, 我想原因是因为它是真正使人们对获得情节的人们产生信任的工具之一。因为他们觉得自己可以看到数据, 所以觉得自己可以理解, 如果你有覆盖的模型, 他们就会知道数据如何进入模型。他们可以对数据进行推理, 我认为这是建立信任的真正关键因素之一。
因此, 现在让我们建立一些散点图以查看其功能。首先, 你将导入一些必需的程序包, 然后导入数据并检出。
请注意, 诸如numpy, pandas, matplotlib和seaborn之类的软件包通常是使用别名导入的, 因此你不必总是键入整个软件包名称, 就像下面的代码块一样:
# Import packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
% matplotlib inline
sns.set()
请记住, Matplotlib将生成图形, 但理想情况下, 你不希望将其发送到文件中。你希望它们在你的笔记本中内联显示, 因此你需要一些IPython魔术来做到这一点:%matplotlib内联。
现在, 你准备导入一些数据并使用.head()方法检查DataFrame的前几行:
# Import data and check out several rows
df = pd.read_csv('data/bc.csv')
df.head()
| 平均半径 | 平均质地 | 平均周长 | 平均面积 | 平均平滑度 | 平均紧密度 | 平均凹度 | 平均凹点 | 平均对称 | 平均分形维数 | … | 最差的质地 | 最差的周长 | 最坏的地方 | 最差的光滑度 | 最差的紧密度 | 最差的凹度 | 最坏的凹点 | 最差的对称性 | 最差分形维数 | 目标 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | 0.07871 | … | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | 0.05667 | … | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | 0.05999 | … | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | 0.09744 | … | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | 0.05883 | … | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0 |
5行×31列
在这种情况下, 你已经导入了乳腺癌(威斯康星州)数据集。但是, 在进入散点图之前, 始终最好使用.info()方法检查DataFrame df中的列名称, 类型和多少个条目:
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 31 columns):
mean radius 569 non-null float64
mean texture 569 non-null float64
mean perimeter 569 non-null float64
mean area 569 non-null float64
mean smoothness 569 non-null float64
mean compactness 569 non-null float64
mean concavity 569 non-null float64
mean concave points 569 non-null float64
mean symmetry 569 non-null float64
mean fractal dimension 569 non-null float64
radius error 569 non-null float64
texture error 569 non-null float64
perimeter error 569 non-null float64
area error 569 non-null float64
smoothness error 569 non-null float64
compactness error 569 non-null float64
concavity error 569 non-null float64
concave points error 569 non-null float64
symmetry error 569 non-null float64
fractal dimension error 569 non-null float64
worst radius 569 non-null float64
worst texture 569 non-null float64
worst perimeter 569 non-null float64
worst area 569 non-null float64
worst smoothness 569 non-null float64
worst compactness 569 non-null float64
worst concavity 569 non-null float64
worst concave points 569 non-null float64
worst symmetry 569 non-null float64
worst fractal dimension 569 non-null float64
target 569 non-null int64
dtypes: float64(30), int64(1)
memory usage: 137.9 KB
通过执行此行代码, 你可以获得各种信息。你会看到, 其中有很多数字数据。在这种情况下, 你可能还想使用.describe()来检查列的摘要统计信息:
df.describe()
| 平均半径 | 平均质地 | 平均周长 | 平均面积 | 平均平滑度 | 平均紧密度 | 平均凹度 | 平均凹点 | 平均对称 | 平均分形维数 | … | 最差的质地 | 最差的周长 | 最坏的地方 | 最差的光滑度 | 最差的紧密度 | 最差的凹度 | 最坏的凹点 | 最差的对称性 | 最差分形维数 | 目标 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 计数 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | … | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 | 569.000000 |
| 意思 | 14.127292 | 19.289649 | 91.969033 | 654.889104 | 0.096360 | 0.104341 | 0.088799 | 0.048919 | 0.181162 | 0.062798 | … | 25.677223 | 107.261213 | 880.583128 | 0.132369 | 0.254265 | 0.272188 | 0.114606 | 0.290076 | 0.083946 | 0.627417 |
| 小时 | 3.524049 | 4.301036 | 24.298981 | 351.914129 | 0.014064 | 0.052813 | 0.079720 | 0.038803 | 0.027414 | 0.007060 | … | 6.146258 | 33.602542 | 569.356993 | 0.022832 | 0.157336 | 0.208624 | 0.065732 | 0.061867 | 0.018061 | 0.483918 |
| 我 | 6.981000 | 9.710000 | 43.790000 | 143.500000 | 0.052630 | 0.019380 | 0.000000 | 0.000000 | 0.106000 | 0.049960 | … | 12.020000 | 50.410000 | 185.200000 | 0.071170 | 0.027290 | 0.000000 | 0.000000 | 0.156500 | 0.055040 | 0.000000 |
| 25% | 11.700000 | 16.170000 | 75.170000 | 420.300000 | 0.086370 | 0.064920 | 0.029560 | 0.020310 | 0.161900 | 0.057700 | … | 21.080000 | 84.110000 | 515.300000 | 0.116600 | 0.147200 | 0.114500 | 0.064930 | 0.250400 | 0.071460 | 0.000000 |
| 50% | 13.370000 | 18.840000 | 86.240000 | 551.100000 | 0.095870 | 0.092630 | 0.061540 | 0.033500 | 0.179200 | 0.061540 | … | 25.410000 | 97.660000 | 686.500000 | 0.131300 | 0.211900 | 0.226700 | 0.099930 | 0.282200 | 0.080040 | 1.000000 |
| 75% | 15.780000 | 21.800000 | 104.100000 | 782.700000 | 0.105300 | 0.130400 | 0.130700 | 0.074000 | 0.195700 | 0.066120 | … | 29.720000 | 125.400000 | 1084.000000 | 0.146000 | 0.339100 | 0.382900 | 0.161400 | 0.317900 | 0.092080 | 1.000000 |
| 最大值 | 28.110000 | 39.280000 | 188.500000 | 2501.000000 | 0.163400 | 0.345400 | 0.426800 | 0.201200 | 0.304000 | 0.097440 | … | 49.540000 | 251.200000 | 4254.000000 | 0.222600 | 1.058000 | 1.252000 | 0.291000 | 0.663800 | 0.207500 | 1.000000 |
8行×31列
除了问自己一些有关正在使用的数据的问题外, 你还应该问自己”什么是数据”?
人们常常会跳入数据集, 而又不知道数据来自何处, 如何收集, 沿袭哪些数据, 等等。在这里查看刚刚导入的数据集的完整描述。
为什么要查看此数据集?你还应该考虑要通过数据分析实现的最终目标!
在这种情况下, 对此的一个潜在答案是, 你正在查看该数据以建立预测诊断的模型。根据数据, 你能否说出肿瘤是良性还是恶性的?
现在该建立一些地块了!让我们建立数据集中前两个特征的散布图, 即平均半径和平均纹理。最好的是, 你可以使用Pandas绘图方法来本地执行此操作!
对于x参数, 你想传入列名”平均半径”。同样, 你将传递”平均纹理”作为y参数:
# Scatter plot of 1st two features
df.plot.scatter(x='mean radius', y='mean texture');

提示:使用分号;禁止从Matplotlib输出文本。
你会看到某种相关性:随着平均半径的增加, 平均纹理也会略微上升。朝向图的右侧有点稀疏。在这一点上, 你不确定它是否是线性的, 但绝对不是高度非线性的。这意味着, 如果你想对数据进行线性建模, 就足够了。但是, 关键是你可以看一下它, 然后思考一下你所看到的内容, 并将其与你最初问自己的原始问题相对比。
在这种情况下, 你需要研究预测肿瘤是良性还是恶性的问题。在这种情况下, 你可能希望散点图由目标着色。你可以通过添加参数c并将其设置为” target”来实现。
# Scatter plot colored by 'target'
df.plot.scatter(x='mean radius', y='mean texture', c='target');

你会看到图中现在有两个清晰的群集。这表明你的数据集的这两个功能在分类肿瘤方面已经非常出色!这已经是一个宝贵的见解!
让我们发现更多散点图。在本教程的前面, 你发现你不能真正确定数据的线性。这是你进行线性回归散点图的绝佳机会, 就像你在以下代码块中所做的一样:
# Scatter plot with linear regression
sns.lmplot(x='mean radius', y='mean texture', data=df)
<seaborn.axisgrid.FacetGrid at 0x108bec390>

在这种情况下, 你可以使用Seaborn的lmplot()绘制”平均半径”和”平均纹理”。还要注意, 你必须将df作为参数传递给绘图函数。现在, 你将看到线性回归遍历该图。你看到的显示在线条旁边的小区域表示置信范围。从这里开始, 你可以计算斜率, 查看纹理如何随半径增加等。
但是, 现在, 你将执行相同的操作, 但是将按目标对其进行着色, 这是诊断:
# Scatter plot colored by 'target' with linear regression
sns.lmplot(x='mean radius', y='mean texture', hue='target', data=df)
<seaborn.axisgrid.FacetGrid at 0x108ab34a8>

现在, 你将看到对应于目标1和目标0的两个子集以及不同的线性回归。现在, 对于目标0, 你具有正线性回归, 而对于目标1, 你具有具有负斜率的线性回归。从统计意义上讲, 这可能并不重要, 但你会看到该图右侧的置信范围实际上很大。
你已经学到了很多有关数据集的知识, 但是现在让我们检查一下你认为可能相关的其他一些功能, 例如”平均半径”和”平均周长”:
df.plot.scatter(x='mean radius', y='mean perimeter', c='target');

你会看到良性和恶性肿瘤之间有一个非常明显的界线, 最重要的是, 你看到的几乎是一条直线。在此数据集中, “平均半径”和”平均周长”高度相关。
这对你意味着什么?
如果以后要使用机器学习模型, 则意味着仅使用这两个功能中的一个就可能做得很好, 因为一个功能中的信息包含在另一个功能中。
但是为什么这很重要?
对于这样的数据集来说, 它可能并不重要, 实际上并没有那么大, 但是当你使用具有成千上万个功能的大数据时, 可能并不重要。在这种情况下, 你可能希望减少数据的维数。这称为”降维”。
还要检查”平均半径”与”平均面积”:
df.plot.scatter(x='mean radius', y='mean area', c='target');

例如, 当你查看该图时, 你就不想使用线性回归对其建模。再次, 你看到散点图提供了有关你可能(不希望)使用的建模技术的大量信息。
现在, 你将构建此数据集的对图。这意味着该图将包含所有要素的所有可能的散点图, 以及沿对角线的直方图。但是首先, 你将对数据进行子集化, 以返回前四列和最后一列:
# Subset your data
df_sub = df.iloc[:, [0, 1, 2, 3, -1]]
现在是时候使用seaborn构建对图了!
sns.pairplot(df_sub, hue='target', size=5);

你现在了解为什么罗杰·彭喜欢散点图吗?使用这些图, 你已经从数据集中提取了大量信息, 并收集了一些有趣的见解, 以了解你可能(不希望)使用哪种建模技术。
接下来:你将发现机器学习决策树的超能力。但是, 这是谁最喜欢的数据科学技术?
预测决策树
在DataFramed的第2集中, 我与AT&T Labs大数据研究助理副总裁Chris Volinksy进行了交谈, 以及周围的话题。他说的是:
我总是对某些旧式技巧的力量感到惊讶。好的老式线性回归仍然是一种非常强大且可解释的, 久经考验的真实技术。它并不总是适当的, 但通常效果很好。决策树是另一种古老的技术, 我总是对它们的工作效果感到惊讶。但是, 你知道, 我总是发现真正强大的一件事是做得很好, 经过深思熟虑的数据可视化。而且, 我非常喜欢在媒体公司中看到的数据可视化类型。
你已经完成了一些数据可视化, 不久之后将进行线性回归。现在, 你将要构建决策树。你将要构建决策树分类器。
那么:什么是决策树分类器?
它是一棵树, 可让你根据特征变量(例如肿瘤的几何尺寸)对数据点(也称为”目标变量”, 例如, 良性或恶性肿瘤)进行分类。看一下这个例子:
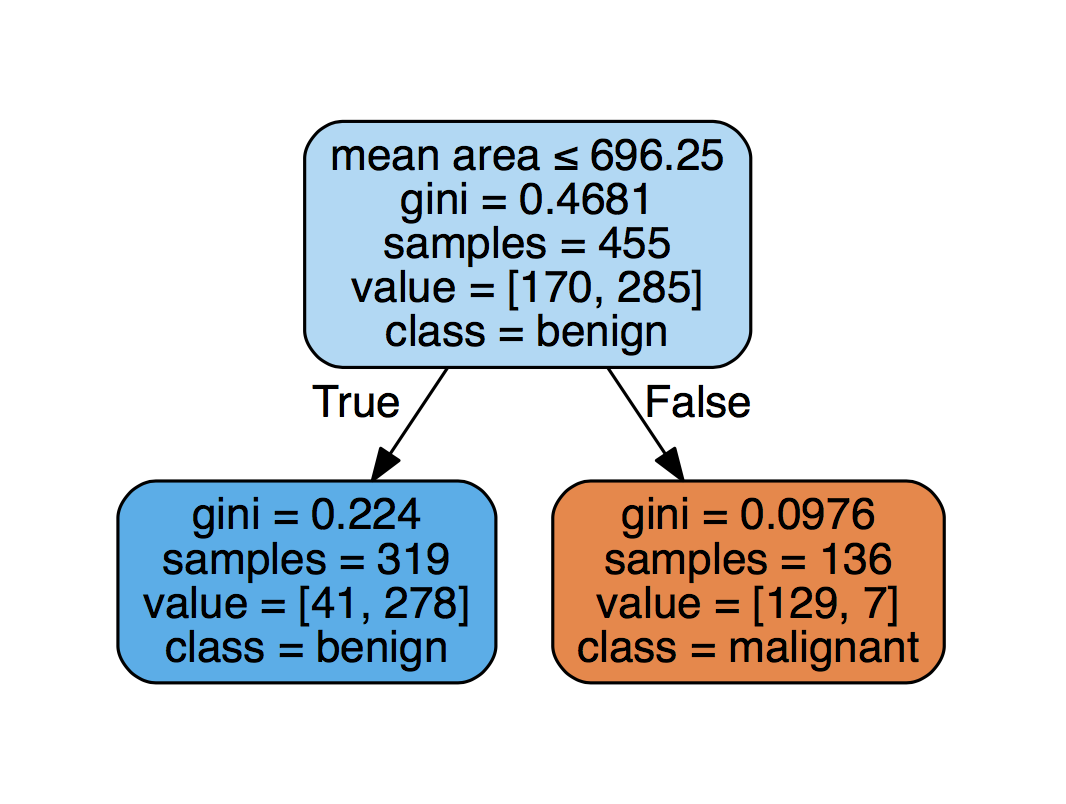
但是, 为什么DataFramed的播客来这样?因为它们是可以解释的!换句话说, 这是
可解释的模型是你可以解释其预测的模型。
这是Cloudera Fast Forward Labs的研究工程师Mike Lee Williams的直接逐字引用(请查看此部分, 其中他谈论了机器学习的可解释性)。
首先, 你需要将这样的模型拟合到训练数据中, 这意味着(基于训练数据)决定哪些决策将在树中的每个分支点进行拆分。例如, 拟合将确定第一个分支在特征”平均面积”上, 并且”平均面积”小于696.25会得出对”良性”的预测。
请注意, 实际上是用于做出这些决定的基尼系数。在这一点上, 你将不再深入研究。
现在让我们构建一个决策树分类器。首先, 你将创建分别包含要素和目标的numpy数组X和y:
X = df_sub.drop('target', axis=1).values
y = df_sub['target'].values
接下来, 你将需要执行以下步骤:
- 你需要在称为训练集的数据子集上拟合(或训练)模型。
- 然后, 你将在另一套测试集上对其进行测试。测试意味着你将对该集合进行预测, 并查看预测的效果如何。
- 你将使用一个称为准确性的度量, 它是正确预测的一部分。
但是, 首先, 你需要使用scikit-learn在训练/测试集中划分数据:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
请注意, 你指定了stratify参数, 以便在测试以及训练数据中保留y的不同值的比例。
现在, 你可以构建决策树分类器。首先使用max_depth = 2创建一个这样的模型, 然后将其拟合为你的数据:
from sklearn import tree
clf = tree.DecisionTreeClassifier(max_depth=2)
clf.fit(X_train, y_train)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2, max_features=None, max_leaf_nodes=None, min_impurity_split=1e-07, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, presort=False, random_state=None, splitter='best')
接下来, 你可以使用.score()方法计算测试集的准确性:
clf.score(X_test, y_test)
0.89473684210526316
为了娱乐, 你还可以在训练集中计算分数:
clf.score(X_train, y_train)
0.90109890109890112
分类器在训练数据上的效果更好, 但这是因为你首先使用此集来构建分类器。
最后, 使用graphviz可视化你的决策树:
import graphviz
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=df_sub.drop('target', axis=1).columns, class_names=['malignant', 'benign'], filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph

线性回归
你已经看到Chris Volinsky是线性回归的忠实拥护者:
但是, 我总是对某些旧式技巧的力量感到惊讶。好的老式线性回归仍然是一种非常强大且可解释的, 久经考验的真实技术。
上面的肿瘤预测任务是分类任务, 你正在尝试对肿瘤进行分类。
另一个众所周知的预测任务称为回归任务, 你要在其中尝试预测数值, 例如给定国家的预期寿命。
让我们导入一些Gapminder数据来做到这一点:
# Import data and check out first rows
df_gm = pd.read_csv('data/gm_2008_region.csv')
df_gm.head()
| 人口 | 生育能力 | 艾滋病毒 | 二氧化碳 | BMI_male | 国内生产总值 | BMI_女性 | 生活 | child_mortality | 区域 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34811059.0 | 2.73 | 0.1 | 3.328945 | 24.59620 | 12314.0 | 129.9049 | 75.3 | 29.5 | 中东和北非 |
| 1 | 19842251.0 | 6.43 | 2.0 | 1.474353 | 22.25083 | 7103.0 | 130.1247 | 58.3 | 192.0 | 撒哈拉以南非洲 |
| 2 | 40381860.0 | 2.24 | 0.5 | 4.785170 | 27.50170 | 14646.0 | 118.8915 | 75.5 | 15.4 | 美国 |
| 3 | 2975029.0 | 1.40 | 0.1 | 1.804106 | 25.35542 | 7383.0 | 132.8108 | 72.5 | 20.0 | 欧洲与中亚 |
| 4 | 21370348.0 | 1.96 | 0.1 | 18.016313 | 27.56373 | 41312.0 | 117.3755 | 81.5 | 5.2 | 东亚和太平洋 |
检查列名称, 类型以及你的DataFrame df_gm中有多少个条目:
df_gm.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 139 entries, 0 to 138
Data columns (total 10 columns):
population 139 non-null float64
fertility 139 non-null float64
HIV 139 non-null float64
CO2 139 non-null float64
BMI_male 139 non-null float64
GDP 139 non-null float64
BMI_female 139 non-null float64
life 139 non-null float64
child_mortality 139 non-null float64
Region 139 non-null object
dtypes: float64(9), object(1)
memory usage: 10.9+ KB
你将使用线性回归模型尝试根据其生育率预测给定国家/地区的预期寿命。但首先, 绘制一个散点图;)
df_gm.plot.scatter(x='fertility', y='life');

但是你可以期望线性模型吗?线性模型将一条直线拟合到数据:
$ y = a_0 + a_1x。$
这再次是一个可解释的模型, 因为它告诉你$ x $的单位增加1导致$ y $的$ a_1 $增加。
现在让我们来看一下这个动作。你将使模型适合整个数据集并可视化回归。请注意, 拟合模型可确定上式中的参数$ a_i $:
# Subset data into feature and target
X_fertility = df_gm[['fertility']].values
y = df_gm[['life']].values
# Import LinearRegression
from sklearn.linear_model import LinearRegression
# Create the regressor: reg
reg = LinearRegression()
# Fit the model to the data
reg.fit(X_fertility, y)
# Plot scatter plot of data
plt.scatter(X_fertility, y)
# Create the prediction space
prediction_space = np.linspace(min(X_fertility), max(X_fertility)).reshape(-1, 1)
# Compute predictions over the prediction space: y_pred
y_pred = reg.predict(prediction_space)
# Plot regression line
plt.plot(prediction_space, y_pred, color='black', linewidth=3);
# Print R^2
print(reg.score(X_fertility, y))
0.619244216774

甚至在你考虑通过使用方程式来求出系数来解释该模型之前, 让我们来看一下绘制的线。如果生育力每增加1单位, 则预期寿命就会下降4.5。不过, 这只是一个估计。
为了使其绝对精确, 你应该从模型中打印出回归系数:
# Print regression coefficient(s)
print(reg.coef_)
[[-4.44387899]]
注意:通常, 你需要在使用回归模型之前对数据进行归一化, 并且可能要使用套索或岭回归等惩罚回归。有关这些技术的更多信息, 请参见srcmini的scikit-learn监督学习课程。
现在, 你可以使用”生育力”和” GDP”两个参数模型进行相同的操作:
$ y = a_0 + a_1x_1 + a_2x_2。
# Extract features from `df_gm`:
X = df_gm[['fertility', 'GDP']].values
# Create the regressor: reg
reg = LinearRegression()
# Fit the model to the data
reg.fit(X, y)
# Print R^2
print(reg.score(X, y))
0.692183492346
# Print regression coefficient(s)
print(reg.coef_)
[[ -3.55717843e+00 1.48369027e-04]]
解释以上回归系数。
但是请稍等。你没有绘制” GDP”图。反对”生命”是什么样的。现在绘制以找出:
df_gm.plot.scatter(x='GDP', y='life');

这绝对不是线性的!但是, 该图仍然非常有趣:GDP介于0到40K之间, 但是值也大于100, 000。是否有用于解决此问题的绘图技术?这个问题的答案实际上是用对数轴绘制数据。你将在下一节中找到有关此数据科学技术的更多信息!
用对数轴绘图
在DataFramed的第6集中, 我采访了srcmini的首席数据科学家David Robinson, 内容涉及公民数据科学。戴夫最喜欢的技术是使用对数轴。
所以这是一种简单的技术, 但是我认为它确实被低估了, 并且确实是我的最爱之一。学习将东西放到对数刻度上。就是说, 从一, 二, 三, 四, 五, 六的数字中选取, 如果可以的话, 比例只能是1、10、100、1000。因此, 在进行嫁接时, 这一点非常重要, 因为在现实世界中, 我们使用的大量数字集规模更大。这些是多个不同的数量级。
现在, 再次绘制”寿命”对” GDP”的图, 但是这次用” GDP”的对数轴:
df_gm.plot.scatter(x='GDP', y='life');
plt.xscale('log')

看起来好多了, 不是吗?现在, 你将获得更有价值的数据, 从而可以更正确地解释数据。
逻辑回归
在DataFramed的第3集中, 我采访了Dstillery首席科学家Claudia Perlich, 在那里她领导了机器学习工作, 该工作有助于定位目标消费者并为营销人员提供见解。我们谈到了数据科学在在线广告世界中的作用, 人类的可预测性, 克劳迪娅(Claudia)的团队如何构建实时出价算法并在线检测到机器人, 以及所有这些不断发展的概念的伦理意义。
今天, 我非常珍惜从逻辑模型(如逻辑回归)中获得的简单性, 优雅性和透明性, 因为在幕后查找和了解可能发生的事情要容易得多。在过去的10到15年中, 这确实成为我的首选工具。实际上, 我使用某种形式的逻辑模型赢得了我所有的数据挖掘比赛。
现在, 在开始之前, 让我们澄清一下:logistic回归是一种线性分类算法。在本节中, 你将使用逻辑回归模型为乳腺癌数据集建立分类预测。
Logistic回归如何工作?
逻辑回归本质上是特征的线性组合
$ t = a_0 + a_1x_1 + a_2x_2 + \ ldots + a_nx_n。
然后将$ t $转换成
$ p = \ frac {1} {1 + e ^ {-t}}。$
现在, 让我们直观地看到从$ t \到p $的转换:
t = np.linspace(-8, 8, 100)
p = 1/(1+np.exp(-t))
plt.plot(t, p);

你将获得此S形函数或S形函数。因此, 如果此线性组合很大, 则$ p $接近1。另一方面, 如果它为负数, 则$ p $接近0。
$ p $是例如肿瘤是恶性的估计概率。换句话说, 如果总和真的接近于1, 则肿瘤发生恶性的可能性很高。类似地, 一个更接近于0的和更可能是肿瘤良性的。
注意:将模型拟合到数据可确定系数$ a_i $。
如果$ p> 0.5 $, 则将目标分类为1(恶性), 否则分类为0(良性)。
该模型如何解释?
好, 重新整理上面的等式
$ a_0 + a_1x_1 + a_2x_2 + \ ldots + a_nx_n = t = \ text {log}(\ frac {p} {1-p})= \ text {logit}(p)$
$ \ frac {p} {1-p} $称为优势比:这是肿瘤恶变的概率超过肿瘤良性的概率。
因此:将$ x_1 $增加1个单位将使赔率比$ \ frac {p} {1-p} $增加$ \ text {exp}(a_1)$个单位。逻辑回归就是这样解释的。它告诉你, 当这些特征改变时, 良性与恶性的相对可能性如何变化。
让我们看看实际情况。
# Check out 1st several rows of data for reacquaintance purposes
df_sub.head()
| 平均半径 | 平均质地 | 平均周长 | 平均面积 | 目标 | |
|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0 |
# Split into features/target
X = df_sub.drop('target', axis=1).values
y = df_sub['target'].values
#Build logistic regression model, fit to training set
from sklearn import linear_model
logistic = linear_model.LogisticRegression()
logistic.fit(X_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
# Compute accuracy on test set
logistic.score(X_test, y_test)
0.91228070175438591
现在打印逻辑回归模型的系数:
logistic.coef_
array([[ 4.52966038, -0.16215141, -0.49868125, -0.02446923]])
使用这些系数, 你会发现”平均纹理”增加1个单位将导致logit(p)降低0.16。这意味着优势比减少exp(0.16)= 1.17或变化0.85倍。
提示:请查看此页面, 以获取有关如何在逻辑回归中解释比值比的更多信息。
现在借助numpy进行计算:
print(np.exp(0.16))
print(1/np.exp(0.16))
1.17351087099
0.852143788966
主成分分析(PCA)
在DataFramed的第8集中, 我与华盛顿大学电子科学研究所的数据科学研究员Jake VanderPlas聊天, 他的工作重点是跨学科的数据密集型物理科学研究。在Python世界中, Jake是《 Python数据科学手册》的作者, 并且活跃于维护和/或贡献于多个著名的Python科学计算软件包, 包括Scikit-learn, Scipy, Matplotlib, Astropy, Altair等。
我一直以来最喜欢的机器学习方法是主成分分析。我只是认为这就像瑞士军刀一样, 你可以用它做任何事情…当我是研究生时, 我很快发现无论何时我与论文顾问会面时, 我都有新的数据集或需要寻找的东西当时, 他要问我的第一个问题是:”好吧, 你做了PCA吗?”
PCA是降维的一个例子, 也是许多工作数据科学家最喜欢的降维方法。重要的是, 例如, 许多数据集拥有太多的功能, 无法放入可伸缩的机器学习管道中, 它可以帮助你减少数据的维数, 同时保留尽可能多的信息。
注意, 实质上, PCA是一种压缩形式。
再次将”平均半径”相对于”平均周长”作图:
df.plot.scatter(x='mean radius', y='mean perimeter', c='target');

现在, 为什么要压缩这些数据, 即缩小到较小的空间?
好吧, 如果你有很多功能和数据, 则可能需要一段时间才能处理所有这些功能。这就是为什么你可能希望预先减小数据的大小。这也称为压缩。如前所述, PCA是实现这种压缩的一种方法。
这个想法是遵循的:如果要素与上面的要素相关联, 那么如果你将其中一个要素扔掉, 则可能会有足够的信息。
有两个基本步骤:
- PCA的第一步是对数据进行解相关, 这对应于数据所在向量空间的线性变换。
- 第二步是实际尺寸减小;真正发生的是, 你的去相关步骤(上述第一步)将要素转换为新的和不相关的要素;然后, 第二步选择包含有关数据的大多数信息的功能(你将尽快对此进行形式化)。
可视化保留许多功能的PCA转换:
# Split original breast cancer data into features/target
X = df.drop('target', axis=1).values
y = df['target'].values
# Scale features
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ar_tot = ss.fit_transform(df)
# Apply PCA
from sklearn.decomposition import PCA
model_tot = PCA()
transformed = model_tot.fit_transform(ar_tot)
print(transformed.shape)
plt.scatter(transformed[:, 0], transformed[:, 1], c=y);
(569, 31)

现在, 使用属性explain_variance_ratio_绘制解释的主成分的总方差与成分数的关系:
plt.plot(np.cumsum(model_tot.explained_variance_ratio_));

前五个组成部分解释了总变化的近90%。此外, 在此图中, 看起来第一个组件解释了多达40%的变化。第一个主要成分包含多少差异?
model_tot.explained_variance_ratio_[0]
0.44896035313223859
现在, 你将通过在逻辑回归之前进行PCA并查看需要使用多少个组件以获得最佳模型性能来获得一些真正的乐趣:
# Split original breast cancer data into features/target
X = df.drop('target', axis=1).values
y = df['target'].values
# Split data into test/train set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=42, stratify=y)
# Build a pipeline of PCA w/ 20 components and a logistic regression
# NOTE: You should also scale your data; this will be an exercise for those
# eager ones out there
from sklearn.pipeline import Pipeline
pca = PCA(n_components=20)
pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])
pipe.fit(X_train, y_train)
pipe.score(X_test, y_test)
0.96491228070175439
现在, 你将为1个组件, 2个组件等等最多30个组件构建PCA /逻辑回归管道。然后, 你将绘制精度与所用组件数量的关系图:
x1 = np.arange(1, 30)
y1 = []
for i in x1:
pca = PCA(n_components=i)
pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])
pipe.fit(X_train, y_train)
y1.append(pipe.score(X_test, y_test))
plt.plot(x1, y1);

随着组件数量的增加, 此模型的性能也会提高。这是因为随着添加更多组件, 你捕获了更多的方差。一旦获得15个组件, 你将无法获得更好的性能。因此, 该数量的组件足以捕获尽可能多的目标。
总结
在本教程中, 你已经导入了两个数据集并进行了探索。此外, 你还了解了六种最喜欢的数据科学技术:
- 你已经了解了散点图的威力以及为何罗杰·彭(Roger Peng)非常喜欢它们。
- 你已经使用了机器学习决策树的超能力。
- 你已经使用了线性回归并探讨了其可解释性。
- 你已经探索了对数轴如何使图更易于阅读。
- 你已经看到了逻辑回归的强大功能。
- 你已经检查了PCA, 这是机器学习的瑞士军刀。
如果你喜欢本教程和Facebook Live会话, 请立即在FB上转发或共享, 然后在Twitter上关注我们:@hugobowne和@srcmini。
 srcmini
srcmini
评论前必须登录!
注册