机器学习回归分析

本文概要

• 回归分析相关的术语
• 为什么要使用回归分析？
• 回归的类型

回归分析是一种用一个或多个自变量来模拟一个因变量(目标变量)和一个独立变量(预测变量)之间关系的统计方法。更具体地说，回归分析帮助我们理解当其他自变量保持不变时，因变量的值是如何与自变量对应变化的。它预测连续的/真实的值，如温度、年龄、工资、价格等。

我们可以使用下面的示例了解回归分析的概念：

例如：假设有一个营销公司a，它每年做各种各样的广告，并以此获得销售额。下面的列表是公司近5年的广告和相应的销售额：

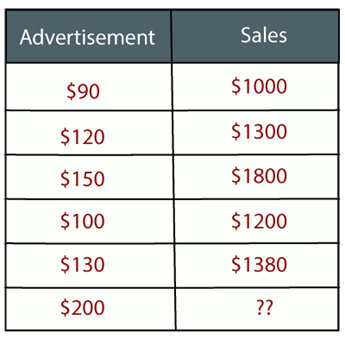
现在，公司想在2019年做200美元的广告，想知道今年的销售预测。因此，为了解决机器学习中的这类预测问题，我们需要回归分析。

回归是一种监督学习技术，它有助于发现变量之间的相关性，并使我们能够预测基于一个或多个预测变量的连续输出变量。它主要用于预测、预测、时间序列建模和确定变量之间的因果关系。

在回归中，我们绘制一个最适合给定数据点的变量之间的图，利用这个图，机器学习模型可以对数据进行预测。简单地说，“回归显示了一条通过目标预测图上所有数据点的直线或曲线，这样数据点与回归线之间的垂直距离最小。”数据点与行之间的距离表示模型是否捕获了强关系。

回归的一些例子为：

• 利用气温及其他因素预测雨量
• 决定市场走势
• 由于鲁莽驾驶而导致交通事故的预测。

回归分析相关的术语

• 因变量：在回归分析，我们要预测或了解的主要因素是所谓的因变量。它也被称为目标变量。
• 独立变量：影响因变量或该因子用于预测因变量被称为自变量，也被称为预测的值。
• 离群值：离群值是一种观测值，与其他观测值相比，它要么包含非常低的值，要么包含非常高的值。异常值可能会妨碍结果，所以应该避免。
• 多重：如果自变量之间的相关性比其他变量高，则这种情况称为多重共线性。它不应该出现在数据集中，因为它在对影响最大的变量进行排序时产生了问题。
• 欠拟合与过拟合：如果我们的算法在训练数据集上运行良好，而在测试数据集上运行不佳，那么这个问题就称为过拟合。如果我们的算法即使使用训练数据集也不能很好地执行，那么这种问题就称为欠拟合。

为什么要使用回归分析？

如前所述，回归分析有助于预测连续变量。在现实世界中有各种各样的场景，我们需要一些未来的预测，如天气状况，销售预测，营销趋势等，在这种情况下，我们需要一些技术，可以做出更准确的预测。因此，在这种情况下，我们需要回归分析，这是一种统计方法，用于机器学习和数据科学。下面是使用回归分析的其他一些原因：

• 回归估计目标和自变量之间的关系。
• 它是用来发现数据中的趋势。
• 它有助于预测真正的/连续的值。
• 通过执行回归，我们可以确定最重要的因素，最不重要的因素，以及每个因素如何影响其他因素。

回归的类型

在数据科学和机器学习中有各种各样的回归。每种类型在不同的情景下都有自己的重要性，但所有回归方法的核心都是分析自变量对因变量的影响。这里我们讨论一些重要的回归类型，如下所示：

• 线性回归
• Logistic回归
• 多项式回归
• 支持向量回归
• 决策树回归
• 随机森林回归
• 岭回归
• 套索回归：

线性回归：

• 线性回归是一种用于预测分析的统计回归方法。
• 它是一种非常简单和容易的算法，用于回归和显示连续变量之间的关系。
• 它是用于在机器学习解决回归问题。
• 线性回归是指自变量(x轴)与因变量(y轴)之间的线性关系，因此称为线性回归。
• 如果只有一个输入变量(x)，那么这种线性回归称为简单线性回归。如果有多个输入变量，则这种线性回归称为多元线性回归。
• 线性回归模型中变量之间的关系可以用下图来解释。这里我们根据员工的工作经验来预测他的工资。

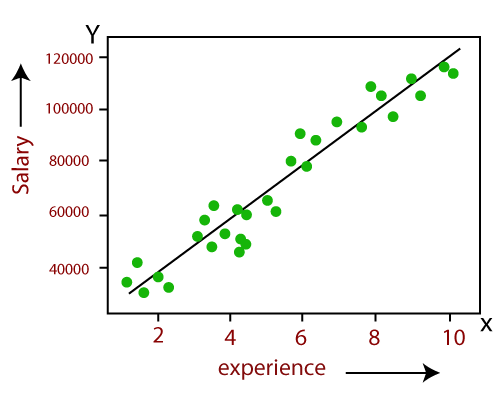
• 下面是线性回归的数学公式：

Y= aX+b

这里，Y =因变量（目标变量），X =独立变量（预测变量），a和b是线性系数

线性回归的一些流行的应用是：

• 趋势分析和销售预测
• 薪酬预测
• 房地产预测
• 在交通的ETA到达。

Logistic回归：

• 逻辑回归是另一种用于解决分类问题的监督学习算法。在分类问题中，我们用二进制或离散格式(如0或1)表示因变量。
• 逻辑回归算法适用于分类变量，如0或1、Yes或No、True或False、Spam或not Spam等。
• 它是一种基于概率概念的预测分析算法。
• 逻辑回归是回归的一种，但在使用上与线性回归算法不同。
• Logistic回归采用s形函数或Logistic函数，是一个复杂的成本函数。这个sigmoid函数用于对逻辑回归中的数据进行建模。函数可以表示为

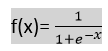
• F（X）= 0和1之间的值输出。
• X =输入到函数
• E =自然对数的底数。

当我们向函数提供输入值(数据)时，它给出如下s曲线：

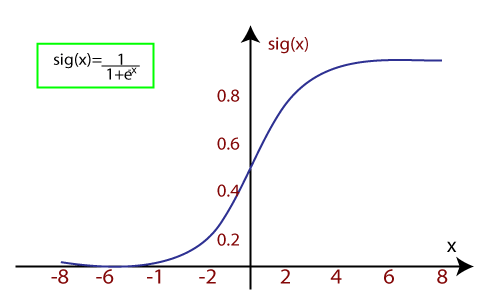
• 它采用阈值电平的概念，高于阈值水平的值向上舍入到1，并且低于阈值电平值被四舍五入为0。

有三种类型的逻辑回归：

• 二进制（0/1，通过/失败）
• 多（猫，狗，狮子）
• 序数（低，中，高）

多项式回归：

• 多项式回归是一种用线性模型对非线性数据集进行建模的回归。
• 它类似于多元线性回归，但它在x的值和y的条件值之间拟合了一条非线性曲线。
• 假设有一个由数据点组成的数据集，数据点以非线性的方式呈现，那么在这种情况下，线性回归并不最适合这些数据点。为了涵盖这些数据点，我们需要多项式回归。
• 在多项式回归中，将原始特征转化为给定次数的多项式特征，然后利用线性模型进行建模。这意味着数据点最好使用多项式线拟合。

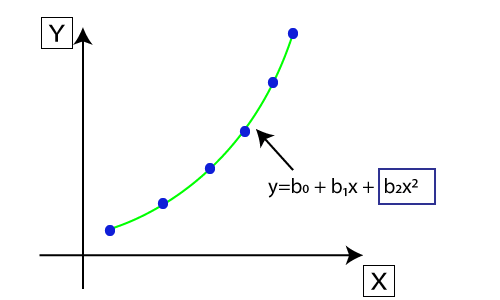
• 多项式回归方程也是由线性回归方程Y= b0+b1x推导而来，即将线性回归方程转为Y= b0+b1x+ b2x^2+ b3x^3+…+ bnx^n。
• 这里Y是预测/目标输出，B0，B1，… BN是回归系数。 x是我们的独立/输入变量。
• 模型仍然是线性的，因为系数仍然是二次的线性

注意：这与多元线性回归不同，在多项式回归中，单个元素具有不同的度数，而不是具有相同度数的多个变量。

支持向量回归：

支持向量机是一种监督学习算法，可用于回归和分类问题。如果我们用它来解决回归问题，那么它就叫做支持向量回归。

支持向量回归是一种回归算法，适用于连续变量。以下是其在支持向量回归中使用的一些关键字：

• 内核：它是一个用于将低维数据映射到高维数据的函数。
• 超平面：支持向量机在一般情况下是两个类之间的一条分离线，而在SVR中则是一条有助于预测连续变量和覆盖大部分数据点的线。
• 边界线：边界线是超平面之外的两条线，这为数据点创建了边界。
• 支持向量：支持向量是最接近超平面和相对类的数据点。

在SVR中，我们总是试图确定具有最大边界的超平面，以便在该边界中覆盖最大数量的数据点。SVR的主要目标是考虑边界线内的最大数据点，而超平面(最佳拟合线)必须包含最大数量的数据点。考虑下面的图像:

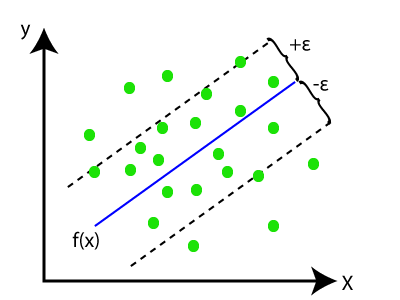
在此，蓝色线被称为超平面，另两条线被称为边界线。

决策树回归：

• 决策树是一种监督学习算法，可用于解决分类和回归问题。
• 它可以解决分类数据和数值数据的问题
• 决策树回归构建了一个树形结构，其中每个内部节点表示一个属性的“测试”，每个分支表示测试的结果，每个叶节点表示最终的决策或结果。
• 从根节点/父节点(数据集)开始构造决策树，它分为左子节点和右子节点(数据集的子集)。这些子节点被进一步划分为它们的子节点，它们自己成为这些节点的父节点。考虑下面的图像:

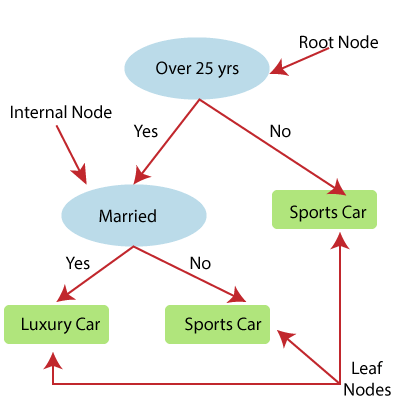
上图展示了决策t回归的例子，在这里，模型试图预测一个人在跑车和豪华车之间的选择。

• 随机森林是最强大的监督学习算法之一，它可以执行回归和分类任务。
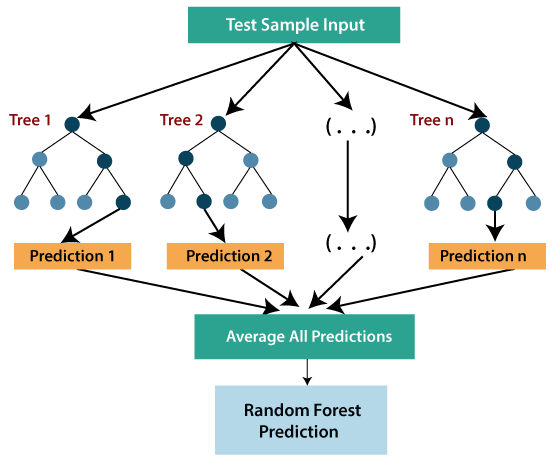
• 随机森林回归是一种综合学习方法，它结合多个决策树，根据每棵树的平均输出来预测最终的输出。组合决策树称为基本模型，它可以更正式地表示为：

g(x)= f0(x)+ f1(x)+ f2(x)+....

• 随机森林使用Bagging或Bootstrap聚集技术进行集成学习，其中聚集的决策树并行运行，互不交互。
• 在随机森林回归的帮助下，我们可以通过创建数据集的随机子集来防止模型中的过拟合。

岭回归：

• 岭回归是线性回归中最稳健的一个版本，它引入了少量的偏差，这样我们就可以得到更好的长期预测。
• 向模型中加入的偏差量称为岭回归惩罚。我们可以计算这个惩罚项通过乘以每个特征的平方权重。
• 岭回归方程为：

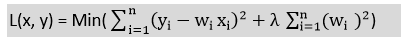
• 如果自变量之间存在高度共线性，一般的线性回归或多项式回归都是失败的，因此可以使用岭回归来解决这类问题。
• 岭回归是一个正则化技术，其被用于降低模型的复杂性。它也被称为L2正规化。
• 如果我们有比样本更多的参数，这有助于解决问题。

套索回归：

• Lasso回归是另一种降低模型复杂度的正则化方法。
• 它类似于岭回归，除了惩罚项只包含绝对权重而不是权重的平方。
• 由于它取绝对值，因此，它可以把斜率缩小到0，而岭回归只能把它缩小到0附近。
• 它也被称为L1正规化。对于套索回归方程为：