线性回归机器学习

本文概要

• 线性回归的类型
• 线性回归线
• 寻找最佳拟合线
• 模型性能
• 线性回归的假设

线性回归是最简单和最流行的机器学习算法之一。它是一种用于预测分析的统计方法。线性回归为继续/实际或数字变量，如销售，薪水，年龄，产品价格等预测。

线性回归算法显示一个相关(y)变量和一个或多个独立(y)变量之间的线性关系，因此称为线性回归。因为线性回归显示的是线性关系，也就是说，它发现因变量的值是如何随着自变量的值而变化的。

线性回归模型提供表示变量之间的关系的倾斜直线。考虑下面的图片：

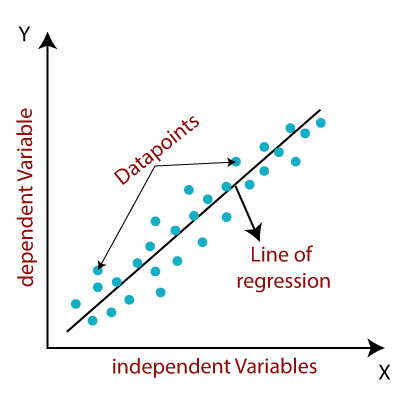
在数学上，我们可以代表一个线性回归为：

y= a0+a1x+ ε

这里，

• Y =因变量（目标变量）
• X =独立变量（预测变量）
• A0 =线的截距（提供了额外的自由度）
• A1 =线性回归系数（比例因子对每个输入值）。
• ε=随机误差

x和y变量的值是用于线性回归模型表示的训练数据集。

线性回归的类型

线性回归可被进一步分为两种类型的算法：

• 简单线性回归：如果用一个单独的自变量来预测一个数值因变量的值，那么这种线性回归算法就称为简单线性回归。
• 多重线性回归：如果用一个以上的自变量来预测一个数值因变量的值，那么这种线性回归算法就称为多元线性回归。

线性回归线

表示因变量和自变量之间关系的直线称为回归线。回归线可以表示两种关系：

• 正线性关系：如果因变量在y轴上增加，自变量在x轴上增加，则这种关系称为正线性关系。

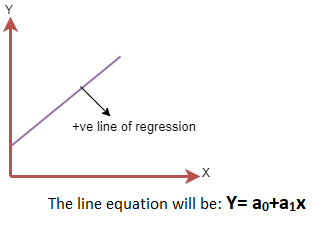
• 负线性关系：如果因变量在y轴上减小，自变量在x轴上增大，则这种关系称为负线性关系。

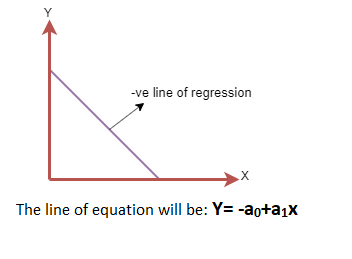
寻找最佳拟合线

当使用线性回归时，我们的主要目标是找到最佳拟合线，这意味着预测值和实际值之间的误差应该最小化。最佳拟合线误差最小。

不同的权值或线的系数(a0, a1)给出了不同的回归线，所以我们需要计算a0和a1的最佳值来找到最佳的拟合线，所以我们使用成本函数来计算。

成本函数

• 线的权值或系数(a0, a1)的不同给出了不同的回归线，并使用成本函数来估计最佳拟合线的系数值。
• 成本函数优化回归系数或权值。它衡量的是线性回归模型的表现。
• 我们可以使用cost函数来求映射函数的精度，该函数将输入变量映射到输出变量。这个映射函数也称为假设函数。

对于线性回归，我们使用均方根误差(MSE)成本函数，它是预测值和实际值之间发生的平方误差的平均值。它可以写成：

对于上述的线性方程，MSE可以计算为：

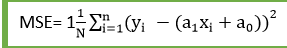
其中，

• N=观察总次数
• Yi =实际值
• (a1xi + a0) =预测价值。

残差：实际值与预测值之间的距离称为残差。如果观测点距离回归直线较远，则残差较大，因此成本函数较大。如果离散点接近回归直线，则残差较小，因此成本函数。

梯度下降：

• 利用梯度下降法，通过计算代价函数的梯度来最小化最小熵。
• 回归模型采用梯度下降法，通过降低成本函数来更新直线的系数。
• 它是通过随机选择系数的值，然后迭代更新这些值以达到最小代价函数。

模型性能

拟合优度决定了回归曲线与观测值的拟合程度。从各种模型中找出最佳模型的过程称为优化。它可以通过以下方法实现：

1. R平方方法：

• R平方是一种决定拟合优度的统计方法。
• 它衡量的是因变量和自变量之间关系的强度，范围为0-100%。
• R平方的高值决定了预测值与实际值之间的差异较小，因此代表了一个好的模型。
• 它也被称为决定系数，或多元回归的多重决定系数。
• 它可以从下面的公式计算：

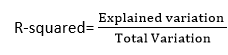
线性回归的假设

下面是一些关于线性回归的重要假设。这些是在构建线性回归模型时的一些正式检查，以确保从给定数据集获得可能的最佳结果。

• 特征与目标之间的线性关系：线性回归假设因变量和自变量之间存在线性关系。
• 特征之间很少或没有多重共线性：多重共线性是指自变量之间的高度相关。由于多重共线性的关系，很难找到预测因子与目标变量之间的真实关系。或者我们可以说，很难确定哪个预测变量影响了目标变量，哪个没有。因此，该模型假设特征或自变量之间很少或没有多重共线性。
• 方差齐性假设：同方差是指所有自变量的误差项都相同的情况。由于具有同方差性，散点图中不应该有清晰的数据模式分布。
• 误差项的正态分布：线性回归假设误差项服从正态分布。如果误差项不是正态分布，那么置信区间就会变得太宽或太窄，这可能会导致寻找系数的困难。可以使用q-q图进行检查。如果曲线是一条直线，没有任何偏差，这意味着误差是正态分布的。
• 无自相关：线性回归模型假设在误差项上没有自相关。如果误差项存在相关性，则会大大降低模型的精度。如果残差之间存在相关性，通常会发生自相关。