机器学习多项式回归

本文概要

• 多项式回归
• 多项式回归模型的公式
• 使用Python多项式回归的实现
• 多项式回归步骤

• 多项式回归是一个回归算法模型从属（Y）之间的关系和自变量（x）的第n个作为多项式。该多项式方程为：下面给出：

y= b0+b1x1+ b2x12+ b2x13+...... bnx1n

• 它也被称为多元线性回归在ML的特殊情况。因为我们的一些多项式项添加到多元线性回归方程将其转化为多项式回归。
• 它是与以提高精度一些变形例的线性模型。
• 在多项式回归用于训练数据集是非线性性质。
• 它利用线性回归模型的拟合复杂和非线性函数和数据集。
• 因此，“以多项式回归，原始特征被转换所需程度（2，3-，…，n）和然后使用线性模型建模成多项式的功能”。

多项式回归

多项式回归的ML需要可以在下面的点来理解：

• 如果我们在一个线性数据集应用线性模型，那么它为我们提供了一个很好的结果，因为我们在简单线性回归所看到的，但如果我们不加任何修改采用同样的模式在非线性数据集，那么它就会产生剧烈的输出。由于其损失函数会增加，错误率会很高，而且精度将降低。
• 因此，对于这样的情况，其中数据点被安排在一个非线性的方式，我们所需要的多项式回归模型。我们可以用线性数据集的对比图和非线性数据集下面以更好的方式理解。

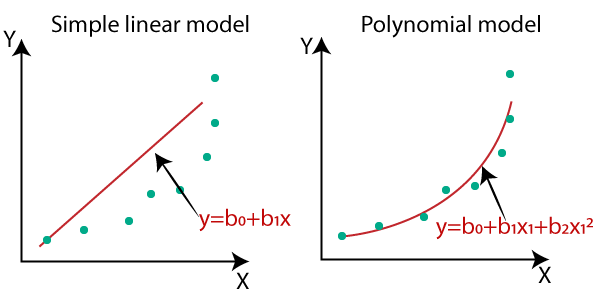
• 在上面的图像，我们采取了被布置非线性的数据集。所以，如果我们用一个线性模型来覆盖它，那么我们就可以清楚地看到，它几乎涵盖了所有的数据点。在另一方面中，曲线是合适的，以覆盖大部分的数据点，这是多项式模型的。
• 因此，如果数据集被安排在一个非线性的方式，那么我们就应该用多元回归模型，而不是简单的线性回归。

注：一个多项式回归算法也被称为多项式线性回归，因为它不依赖于变量，相反，它取决于系数，它们布置在一个线性方式。

多项式回归模型的公式

简单线性回归方程：Y = B0 + B1X ………（a）中

多重线性回归方程：Y = B0 + B1X + b2x2 + b3x3 + …. + bnxn ………（b）中

多项式回归方程：Y = B0 + B1X + b2x2 + b3x3 + …. + bnxn ……….（c）中

当我们比较上面三个方程，我们可以清楚地看到，所有这三个方程是多项式方程而是通过变量的程度有所不同。简单和多元线性方程也多项式方程与单个度，和多项式回归方程是线性方程与第n个程度。因此，如果我们一定程度添加到我们的线性方程组，然后将它转换成多项式线性方程。

注：为了更好地理解多项式回归，你必须有简单线性回归的知识。

使用Python多项式回归的实现

在这里，我们将使用Python实现多项式回归。我们将通过与简单线性回归模型比较多项式回归模型的理解。因此，首先，让我们了解我们所要构建模型的问题。

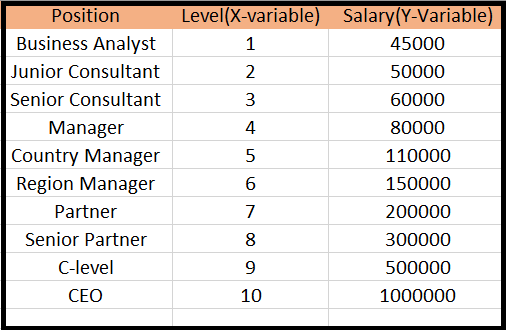
问题描述：有一个人力资源公司，这是要聘请一位新的候选人。候选人告诉他以前的每年薪水160K，和HR必须检查他是否说的是真话还是虚张声势。因此，要确定这一点，他们只拥有他以前在排名前10位的薪酬与他们的水平提到公司的数据集。通过检查数据集可用，我们已经发现，在位置的水平和薪酬之间的非线性关系。我们的目标是建立一个唬人探测器回归模型，让HR可以聘请一位诚实的求职者。下面是建立这样一个模型的步骤。

多项式回归步骤

参与多项式回归的主要步骤给出如下：

• 数据预处理
• 建立一个线性回归模型，其安装到数据集
• 构建多元回归模型，并要将其安装到数据集
• 可视化的线性回归和多元回归模型的结果。
• 预测的输出。

注：在这里，我们将建立线性回归模型，以及多项式回归，看看预测的结果。和线性回归模型以供参考。

数据预处理步骤：

数据预处理步骤将保持不变，如以前的回归模型，除了一些变化。在多元回归模型，我们将不使用的功能扩展，并且还我们不会我们的数据分割为训练和测试集。它有两方面的原因：

• 该数据集包含非常少的信息，这是不适合将其分为测试和训练集，否则我们的模型将无法找到薪水和级别之间的关系。
• 在这个模型中，我们要对薪水很准确的预测，所以模型应该有足够的信息。

用于预处理步骤的代码给出如下：

# importing libraries
import numpy as nm
import matplotlib.pyplot as mtp
import pandas as pd

#importing datasets
data_set= pd.read_csv('Position_Salaries.csv')

#Extracting Independent and dependent Variable
x= data_set.iloc[:，1:2].values
y= data_set.iloc[:，2].values

说明：

• 在上面的代码行，我们有进口的重要Python库导入数据集，并对其进行操作。
• 接下来，我们导入数据集“Position_Salaries.csv”，其中包含三列（位置，级别和工资），但我们会考虑只在两列（工资和级别）。
• 在此之后，我们已经提取从数据集的从属（Y）和自变量（X）。用于x变量，我们采取参数[：，1：2]，因为我们要1个指数（水平），并包括：2，使之作为基质。

输出：

通过执行上面的代码，我们可以看到我们的数据为：

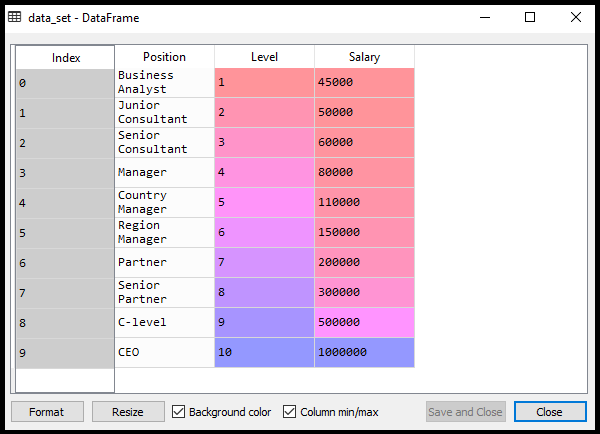
正如我们可以在上面输出看到的，有三列存在（位置，等级和薪水）。但是，我们只考虑两列，因为位置等同于水平或可被视为位置的编码形式。

在这里，我们将预测为6.5级的输出，因为候选人有4年以上作为一个区域经理的经历，所以他一定在7级和6之间。

构建线性回归模型：

现在，我们将建立和适应线性回归模型的数据集。在建设多项式回归，我们将采取线性回归模型为基准，二者的结果进行比较。该代码下面给出：

#Fitting the Linear Regression to the dataset
from sklearn.linear_model import LinearRegression
lin_regs= LinearRegression()
lin_regs.fit(x，y)

在上面的代码中，我们使用线性回归类的lin_regs对象并将它装配到数据集的变量（x和y）中创建的简单的线性模型。

输出：

Out[5]: LinearRegression(copy_X=True，fit_intercept=True，n_jobs=None，normalize=False)

构建多项式回归模型：

现在，我们将建立多元回归模型，但它会从简单的线性模型略有不同。因为在这里，我们将使用PolynomialFeatures类预处理库。我们使用这个类来一些额外的功能添加到我们的数据集。

#Fitting the Polynomial regression to the dataset
from sklearn.preprocessing import PolynomialFeatures
poly_regs= PolynomialFeatures(degree= 2)
x_poly= poly_regs.fit_transform(x)
lin_reg_2 =LinearRegression()
lin_reg_2.fit(x_poly，y)

在上面的代码行中，我们使用poly_regs.fit_transform（x）时，因为第一，我们提供了特征矩阵转换成多项式特征矩阵，然后将其装配到多项式回归模型。参数值（度= 2）取决于我们的选择。我们可以根据我们的多项式的特点进行选择。

执行代码后，我们会得到另一个矩阵x_poly，它可以变资源管理器选项下可以看到：

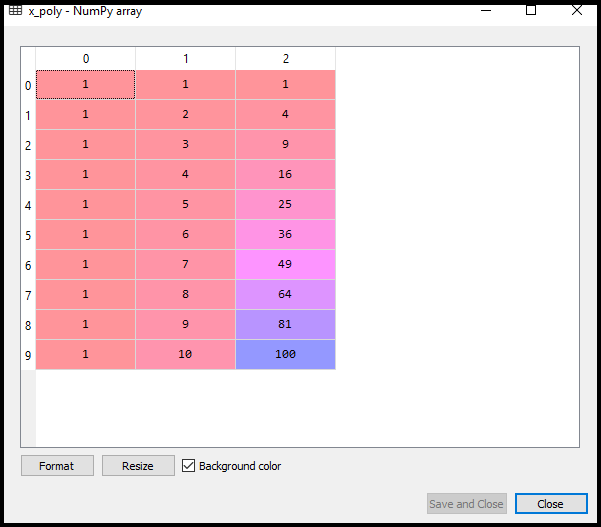
接下来，我们用另一种线性回归的对象，即lin_reg_2，以适应我们x_poly向量的线性模型。

输出：

Out[11]: LinearRegression(copy_X=True，fit_intercept=True，n_jobs=None，normalize=False)

可视化线性回归结果：

现在，当我们在简单线性回归做，我们将可视化的线性回归模型的结果。下面是它的代码：

#Visulaizing the result for Linear Regression model
mtp.scatter(x，y，color="blue")
mtp.plot(x，lin_regs.predict(x)，color="red")
mtp.title("Bluff detection model(Linear Regression)")
mtp.xlabel("Position Levels")
mtp.ylabel("Salary")
mtp.show()

输出：

在上面的输出图像中，我们可以清楚地看到，回归线是从数据集为止。预测是在一个红色的直线，蓝点是实际值。如果我们考虑这个输出预测CEO的价值，它会给一个大约的薪水。 600000 $，这是远离真正的价值。

因此，我们需要一个曲面模型，以适应比直线其他数据集。

对于可视化多项式回归结果

在这里，我们将可视化多项式回归模型，代码是从上述模型略有不同的结果。

该代码下面给出：

#Visulaizing the result for Polynomial Regression
mtp.scatter(x，y，color="blue")
mtp.plot(x，lin_reg_2.predict(poly_regs.fit_transform(x))，color="red")
mtp.title("Bluff detection model(Polynomial Regression)")
mtp.xlabel("Position Levels")
mtp.ylabel("Salary")
mtp.show()

在上面的代码，我们采取lin_reg_2.predict（poly_regs.fit_transform（X），而不是x_poly，因为我们希望有一个线性回归对象预测多项式特征矩阵。

输出：

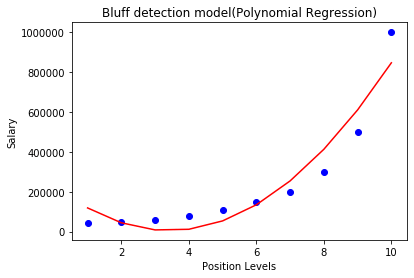
正如我们上面的输出图像中看到，该预测是接近真实值。上述情节可能会有所不同，因为我们将改变程度。

对于度= 3：

如果我们改变度= 3，那么我们将给出更精确的曲线图，如图所示，下面图像英寸

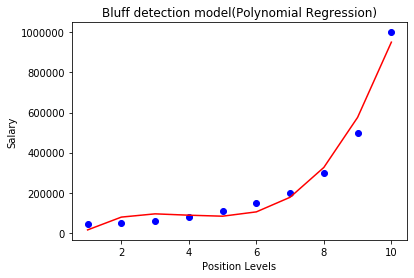
从而我们可以看到上面的输出图像在这里，为6.5级的预测薪水接近170K $ -190k $，这似乎是未来的员工是怎么说他的工资的真相。

度= 4：让我们再次程度更改为4，现在将得到最准确的情节。因此，我们可以通过增加多项式的程度得到更准确的结果。

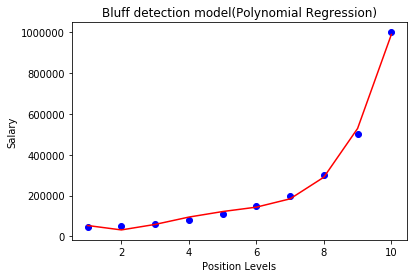
预测与线性回归模型的最终结果：

现在，我们将使用线性回归模型，看员工是否在说真话还是虚张声势预测最终输出。因此，对于这一点，我们将使用预测（）方法，并传递值6.5。下面是它的代码：

lin_pred = lin_regs.predict([[6.5]])
print(lin_pred)

输出：

[330378.78787879]

与预测多元回归模型的最终结果：

现在，我们将用多元回归模型，线性模型进行对比预测最终输出。下面是它的代码：

poly_pred = lin_reg_2.predict(poly_regs.fit_transform([[6.5]]))
print(poly_pred)

输出：

[158862.45265153]

正如我们所看到的，对于多项式回归预测的输出为[158862.45265153]，这是更接近实际价值，因此，我们可以说，未来的员工是说真的。