支持向量机（SVM）算法

本文概要

• SVM的类型
• 超平面和支持向量的SVM算法
• SVM如何工作？

支持向量机或SVM是最流行的监督学习算法，用于分类和回归的问题之一。然而，主要是，它是用于在机器学习分类问题。

支持向量机算法的目标是创造最好的线路或决策边界，可以分离n维空间划分为类，使我们可以很容易地把新的数据点在未来正确的类别。这个最佳决策边界被称为超平面。

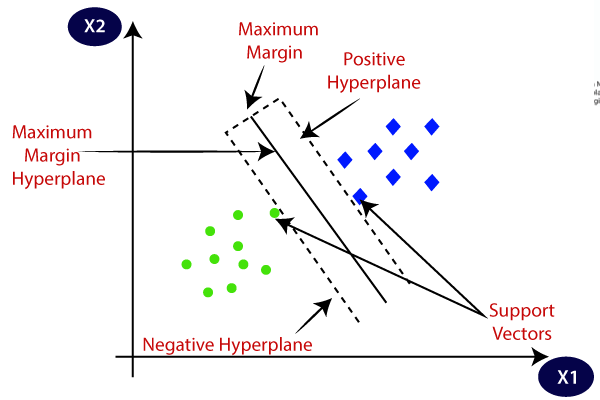
SVM选择极值点/载体，在创建超平面的帮助。这些极端的情况下被称为支持向量，因此算法被称为支持向量机。考虑下面的图，其中有一些是使用决策边界或超平面分为两个不同的类别：

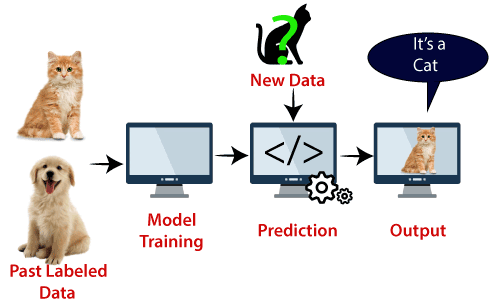
例如：SVM可以与我们在KNN分类已经使用了示例来理解。假设我们看到一个奇怪的猫也有狗的一些功能，所以如果我们想有一个模型，可以准确地确定其是否是猫或狗，所以这种模式可以通过使用SVM算法创建。首先，我们将培养我们，有很多猫，狗的图像，模型，以便它可以了解猫狗的不同特点，然后我们用这个奇怪的生物测试。因此，作为支持向量创建这两个数据之间（猫，狗）判定边界的，选择极端的情况下（支持向量），它会看到猫，狗的极端情况。在支持向量的基础上，将其分类为一只猫。请看下图：

SVM算法可用于人脸检测，图像分类，文本分类等

SVM的类型

SVM可以有两种类型：

• 线性SVM：线性SVM用于线性可分数据，这意味着如果一个数据集可以通过使用单个直线被分类成两个类，则这样的数据被称为线性可分数据，和分类器称为线性SVM分类器。
• 非线性SVM：非线性SVM用于非线性分离的数据，这意味着如果一个数据集不能通过使用一个直线被分类，那么这样的数据被称为非线性数据和用于分类器被称为非线性SVM分类器。

超平面和支持向量的SVM算法

超平面：可以有多个线/决策界偏析在n维空间中的类，但我们需要找出最好的决策边界，有助于数据点进行分类。这个最佳边界被称为SVM的超平面。

超平面的尺寸取决于如果有2个特征（如图图像）的存在于所述数据集，该装置的特征，然后超平面将是一条直线。并且如果有3个特征，则超平面将是一个2维平面。

我们始终创建一个具有最大利润，这意味着数据点之间的最大距离的超平面。

支持向量：

是最接近于超平面和该数据点或向量影响超平面的位置被称为支持向量。由于这些载体支持超平面，因此被称为支持向量。

SVM如何工作？

线性SVM：

所述SVM算法的工作可以通过使用一个例子来理解。假设我们有一个具有两个标签（绿色和蓝色）的数据集，而该数据集有两个特点x1和x2。我们希望有一个分类，可坐标对（X1，X2）进行分类绿色或蓝色。考虑下面的图片：

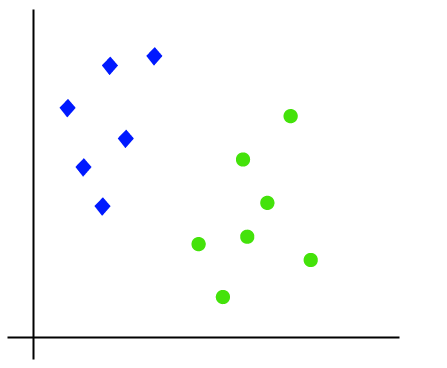
所以，因为它是2-d空间，因此通过只使用一条直线，我们可以很容易地这两个类分开。但有一点是多行，可以分离这些类。考虑下面的图片：

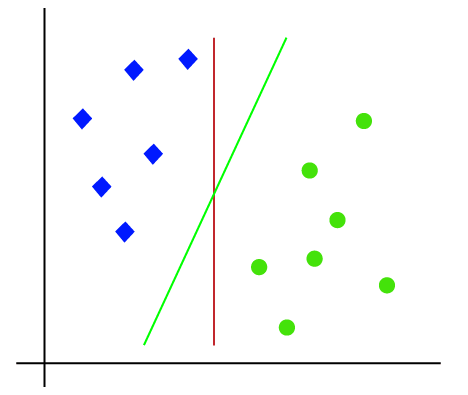
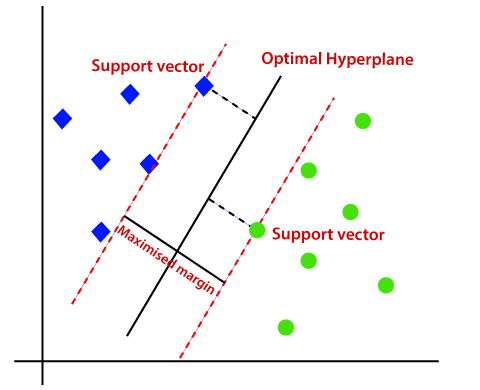
因此，SVM算法有助于找到最好的线路或决策边界;这个最好的边界或区域被称为超平面。 SVM算法找到来自两个班线的最近点。这些点被称为支持向量。的矢量和所述超平面之间的距离被称为余量。和SVM的目标是最大化这一保证金。最大余量的超平面称为最优超平面。

非线性SVM：

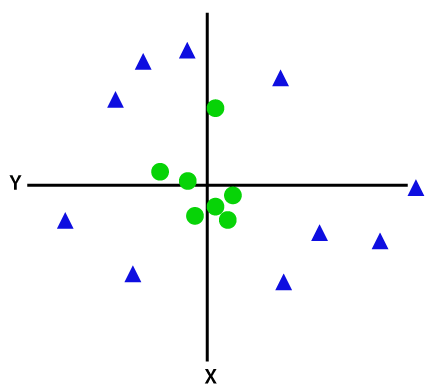
如果数据是线性排列的，那么我们可以通过使用直线分开，但对非线性数据，我们不能画一条直线。考虑下面的图片：

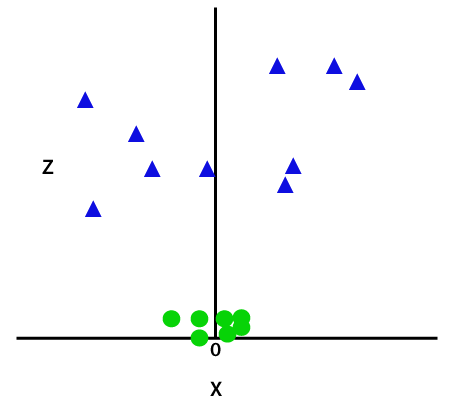
因此，这些数据点分开，我们需要增加一个维度。对于线性数据，我们已经使用两个维度x和y，所以对于非线性数据，我们将添加的第三尺寸Z。它可以计算为：

z=x2 +y2

通过将第三尺寸，所述样品空间将变得如下图像：

所以，现在，SVM将分集成类以下列方式。考虑下面的图片：

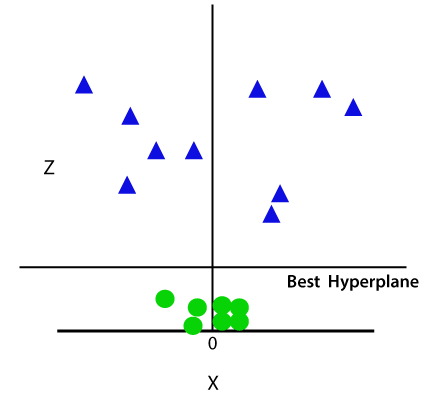
由于我们是在3-d的空间，因此它看起来像平行于x轴的平面。如果我们用Z = 1二维空间的转换，然后它会成为为：

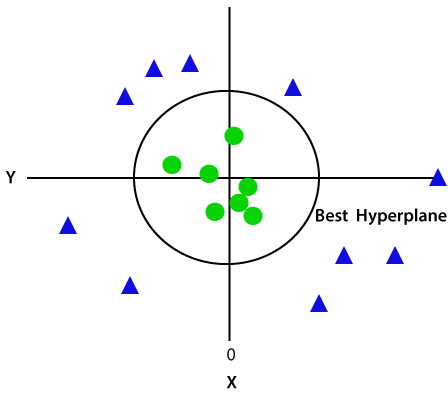
因此，我们在非线性数据的情况下得到半径为1的周围。

支持向量机的Python实现

现在，我们将使用Python实现SVM算法。在这里，我们将使用相同的数据集USER_DATA，我们在Logistic回归和KNN分类已经使用。

• 数据前处理步骤

直到数据预处理步骤，代码将保持不变。下面是代码：

#Data Pre-processing Step
# importing libraries
import numpy as nm
import matplotlib.pyplot as mtp
import pandas as pd

#importing datasets
data_set= pd.read_csv('user_data.csv')

#Extracting Independent and dependent Variable
x= data_set.iloc[:，[2，3]].values
y= data_set.iloc[:，4].values

# Splitting the dataset into training and test set.
from sklearn.model_selection import train_test_split
x_train，x_test，y_train，y_test= train_test_split(x，y，test_size= 0.25，random_state=0)
#feature Scaling
from sklearn.preprocessing import StandardScaler  
st_x= StandardScaler()  
x_train= st_x.fit_transform(x_train)  
x_test= st_x.transform(x_test)

执行上面的代码后，我们将预先处理数据。该代码会给出的数据集为：

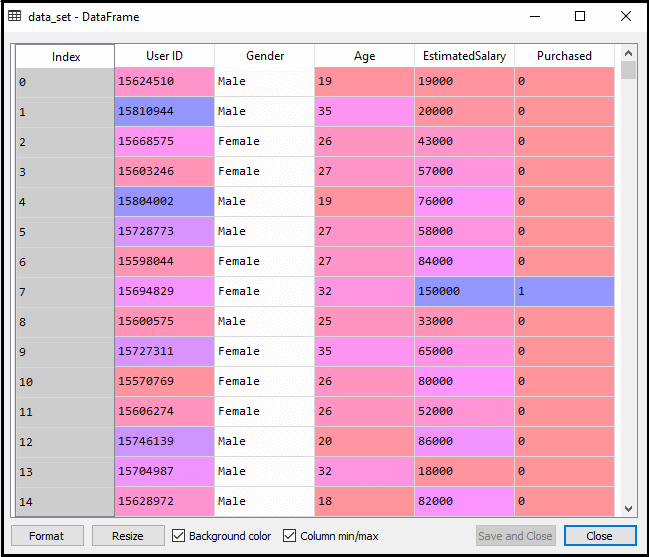
对于测试集合中的缩放的输出将是：

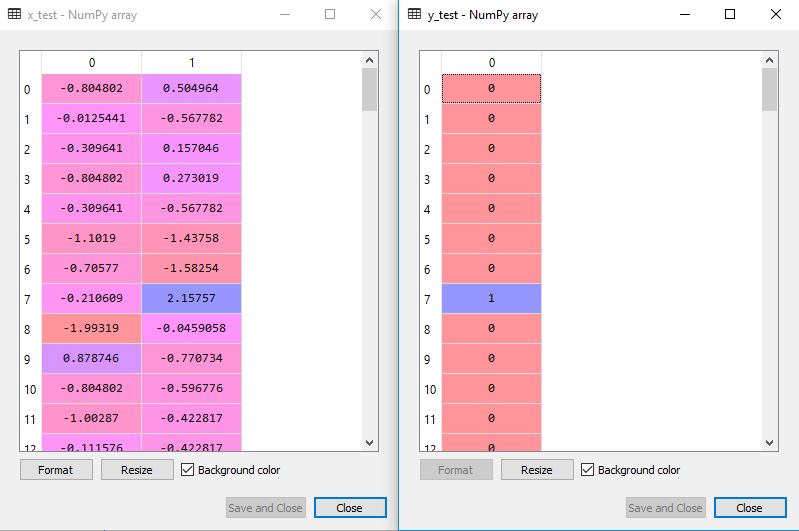
拟合SVM分类训练集：

现在的训练集将被安装到SVM分类。要创建SVM分类，我们会从Sklearn.svm库中导入SVC类。下面是它的代码：

from sklearn.svm import SVC # "Support vector classifier"
classifier = SVC(kernel='linear'，random_state=0)
classifier.fit(x_train，y_train)

在上面的代码中，我们使用的内核=“线性”，如在这里我们创建用于线性可分数据SVM。但是，我们可以将其更改为非线性的数据。然后我们安装在分类的训练数据集（x_train，y_train）

输出：

Out[8]: 
SVC(C=1.0，cache_size=200，class_weight=None，coef0=0.0，decision_function_shape='ovr'，degree=3，gamma='auto_deprecated'，kernel='linear'，max_iter=-1，probability=False，random_state=0，shrinking=True，tol=0.001，verbose=False)

该模型性能可以通过改变C（正则化因子），γ和内核的值被改变。

• 预测测试集的结果：现在，我们将预测测试集的输出。对于这一点，我们将创建y_pred一个新的载体。下面是它的代码：

#Predicting the test set result
y_pred= classifier.predict(x_test)

得到y_pred向量后，我们可以比较的y_pred结果和y_test检查实际值与预测值之间的差异。

输出：下面是输出为测试组的预测：

• 创建混淆矩阵：现在我们来看看SVM分类的是多少不正确的预测都存在相比，Logistic回归分类器的性能。要创建混淆矩阵，我们需要导入sklearn库的confusion_matrix功能。导入功能后，我们将使用一个新的变量厘米调用它。这个函数有两个参数，主要y_true（实际值）和y_pred（由分类目标价值回归）。下面是它的代码：

#Creating the Confusion matrix
from sklearn.metrics import confusion_matrix
cm= confusion_matrix(y_test，y_pred)

输出：

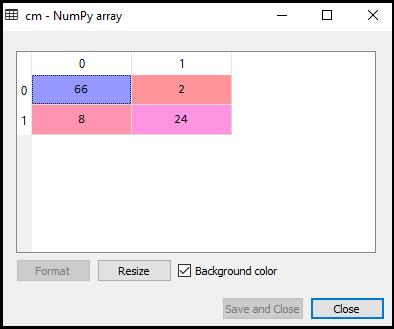
正如我们可以在上述输出图像中看到的，有66 + 24 = 90个正确的预测和8 + 2 = 10个正确的预测。因此，我们可以说，相比于Logistic回归模型我们的SVM模型改进。

• 可视化训练集的结果：现在，我们将可视化训练集的结果，下面是它的代码：

from matplotlib.colors import ListedColormap
x_set，y_set = x_train，y_train
x1，x2 = nm.meshgrid(nm.arange(start = x_set[:，0].min() - 1，stop = x_set[:，0].max() + 1，step  =0.01)，nm.arange(start = x_set[:，1].min() - 1，stop = x_set[:，1].max() + 1，step = 0.01))
mtp.contourf(x1，x2，classifier.predict(nm.array([x1.ravel()，x2.ravel()]).T).reshape(x1.shape)，alpha = 0.75，cmap = ListedColormap(('red'，'green')))
mtp.xlim(x1.min()，x1.max())
mtp.ylim(x2.min()，x2.max())
for i，j in enumerate(nm.unique(y_set)):
    mtp.scatter(x_set[y_set == j，0]，x_set[y_set == j，1]，c = ListedColormap(('red'，'green'))(i)，label = j)
mtp.title('SVM classifier (Training set)')
mtp.xlabel('Age')
mtp.ylabel('Estimated Salary')
mtp.legend()
mtp.show()

输出：

通过执行上面的代码，我们将得到的输出：

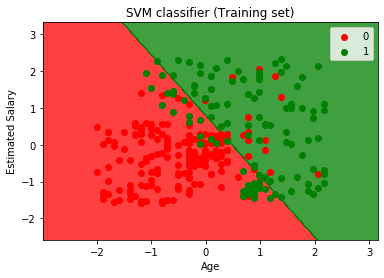
正如我们所看到的，上面的输出出现类似Logistic回归输出。在输出中，我们得到的直线作为超平面，因为我们使用的分类器的线性内核。同时，我们也高于对于2D空间，在SVM的超平面为直线讨论。

• 可视化测试集的结果：

#Visulaizing the test set result
from matplotlib.colors import ListedColormap
x_set，y_set = x_test，y_test
x1，x2 = nm.meshgrid(nm.arange(start = x_set[:，0].min() - 1，stop = x_set[:，0].max() + 1，step  =0.01)，nm.arange(start = x_set[:，1].min() - 1，stop = x_set[:，1].max() + 1，step = 0.01))
mtp.contourf(x1，x2，classifier.predict(nm.array([x1.ravel()，x2.ravel()]).T).reshape(x1.shape)，alpha = 0.75，cmap = ListedColormap(('red'，'green' )))
mtp.xlim(x1.min()，x1.max())
mtp.ylim(x2.min()，x2.max())
for i，j in enumerate(nm.unique(y_set)):
    mtp.scatter(x_set[y_set == j，0]，x_set[y_set == j，1]，c = ListedColormap(('red'，'green'))(i)，label = j)
mtp.title('SVM classifier (Test set)')
mtp.xlabel('Age')
mtp.ylabel('Estimated Salary')
mtp.legend()
mtp.show()

输出：

通过执行上面的代码，我们将得到的输出：

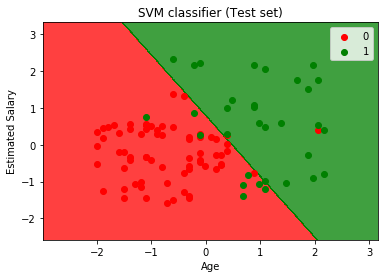
正如我们可以在上述输出图像中所看到的，SVM分类划分了用户分为两个区域（购买或不购买）。谁购买了SUV用户在与红散点的红色区域。而谁没有购买SUV的用户均符合绿色散点的绿色区域。超平面有两个班分为购买和没有购买变量。