本文概要
- 朴素贝叶斯算法是一种监督学习算法,该算法是基于贝叶斯定理,并用于解决分类问题。
- 它主要用于在包括高维训练数据集文本分类。
- 朴素贝叶斯分类器是简单和最有效的分类算法,它有助于建立快速的机器学习模型,可以做出快速的预测之一。
- 这是一个概率分类,它预测的对象的概率的基础上,该装置。
- 朴素贝叶斯算法的一些最典型的例子是垃圾邮件过滤,青涩分析和分类的文章。
为什么叫朴素贝叶斯?
朴素贝叶斯算法由两个词语朴素贝叶斯和,其可被描述为:
- Naive:之所以称为Naive,是因为它假设某个特性的出现独立于其他特性的出现。例如,如果水果是根据颜色、形状和味道来识别的,那么红色、球形和甜的水果就是苹果。因此,每个特性都各自有助于识别它是否是苹果,而不依赖于其他特性。
- 贝叶斯:之所以叫贝叶斯是因为它依赖于贝叶斯定理的原理。
贝叶斯定理
- 贝叶斯定理也被称为贝叶斯法则或贝叶斯定律,这是用来确定与先前知识假设的概率。这取决于条件概率。
- 对贝叶斯定理的公式给出如下:
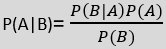
哪里,
P(A | B)是后验概率:在观察到的事件B.假设A的概率
P(B | A)是可能性概率:所提供的证据的概率是一个假设的概率是真实的。
P(A)是先验概率:观察证据之前假设的概率。
P(B)是边缘概率:证据概率。
朴素贝叶斯分类器的工作
朴素贝叶斯分类器的工作可以用下面的例子来理解:
假设我们有天气状况的数据集和相应的目标变量“播放”。因此,使用此数据集,我们需要决定是否应根据天气情况在某一天玩与否。因此,要解决这个问题,我们需要遵循以下步骤:
- 转换给定数据集为频率表。
- 通过查找的功能给出的概率产生似然表。
- 现在,使用贝叶斯定理来计算后验概率。
问题:如果天气晴朗,那么球员应该发挥或没有?
解决方法:要解决这个问题,首先考虑下面的数据集:
| 外表 | 玩 | |
|---|---|---|
| 0 | Rainy | 是 |
| 1 | Sunny | 是 |
| 2 | Overcast | 是 |
| 3 | Overcast | 是 |
| 4 | Sunny | 没有 |
| 5 | Rainy | 是 |
| 6 | Sunny | 是 |
| 7 | Overcast | 是 |
| 8 | Rainy | 没有 |
| 9 | Sunny | 没有 |
| 10 | Sunny | 是 |
| 11 | Rainy | 没有 |
| 12 | Overcast | 是 |
| 13 | Overcast | 是 |
对于天气状况的频率表:
| Weather | Yes | 没有 |
| Overcast | 5 | 0 |
| Rainy | 2 | 2 |
| Sunny | 3 | 2 |
| Total | 10 | 五 |
似然表气象条件:
| Weather | No | 是 | |
| Overcast | 0 | 5 | 5/14= 0.35 |
| 多雨的 | 2 | 2 | 4/14 = 0.29 |
| Sunny | 2 | 3 | 5/14=0.35 |
| All | 4/14 = 0.29 | 10/14=0.71 |
应用Bayes原理:
P(是|晴朗)= P(阳光|是)* P(是)/ P(阳光)
P(阳光|是)= 3/10 = 0.3
P(晴天)= 0.35
P(是)= 0.71
所以P(是|阳光)= 0.3 * 0.71 / 0.35 = 0.60
P(无|阳光)= P(阳光|否)* P(否)/ P(阳光)
P(阳光| NO)= 2/4 = 0.5
P(否)= 0.29
P(晴天)= 0.35
所以P(无|晴朗)= 0.5 * 0.29 / 0.35 = 0.41
所以,我们可以从上述计算看出,P(是|阳光)> P(无|阳光)
因此,在一个阳光明媚的日子,玩家可以玩游戏。
朴素贝叶斯分类器的优点:
- 朴素贝叶斯是的快速和容易ML算法来预测一类数据集之一。
- 它可用于二进制和多级分类。
- 相比于其他算法它在多类预测表现良好。
- 它是文本分类问题的最流行的选择。
朴素贝叶斯分类器的缺点:
- 朴素贝叶斯假设所有的功能是独立的或不相关的,所以它不能学特征之间的关系。
朴素贝叶斯分类器的应用:
- 它是用于信用评分。
- 它在医学数据分类使用。
- 它可以实时预测中使用,因为朴素贝叶斯分类器是一个渴望学习。
- 它是在文本分类使用诸如垃圾邮件过滤和情绪分析。
朴素贝叶斯模型的类型
有三种类型的朴素贝叶斯模型,其给出如下:
- 高斯:高斯模型假设特征服从正态分布。这意味着如果预测取连续值,而不是离散的,则模型假定这些值是从高斯分布进行采样。
- 多项式:当数据是多项式分布多项式朴素贝叶斯分类器。它主要用于文档分类的问题,这意味着特定文档所属的类别,例如体育,政治,教育,等等。分类器使用的预测单词的频率。
- 伯努利:伯努利分类的工作原理类似于多项分类,但预测变量是独立的布尔变量。例如,如果一个特定的单词存在或不存在中的文档。这种模式也是著名的文档分类的任务。
朴素贝叶斯算法的Python实现
现在,我们将使用Python实现一个朴素贝叶斯算法。因此,对于这一点,我们将使用“用户 – 数据”的数据集,这是我们在其他分类模型已经使用。因此,我们可以轻松地比较与其他车型的朴素贝叶斯模型。
步骤来实现:
- 数据前处理步骤
- 装修朴素贝叶斯训练集
- 预测测试结果
- 结果的测试精度(混淆矩阵的创建)
- 可视化测试集的结果。
1)数据预处理步骤:
在这一步中,我们将预处理/准备数据,使我们可以在我们的代码有效地使用它。正如我们在数据预处理做的是类似的。这样做的代码下面给出:
Importing the libraries
import numpy as nm
import matplotlib.pyplot as mtp
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('user_data.csv')
x = dataset.iloc[:,[2,3]].values
y = dataset.iloc[:,4].values
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train = sc.fit_transform(x_train)
x_test = sc.transform(x_test)在上面的代码中,我们使用“数据集= pd.read_csv(‘user_data.csv’)加载的数据集到我们的程序。装载的数据集被分成训练集和测试集,然后我们已缩放的特征变量。
DataSet的输出给出如下:
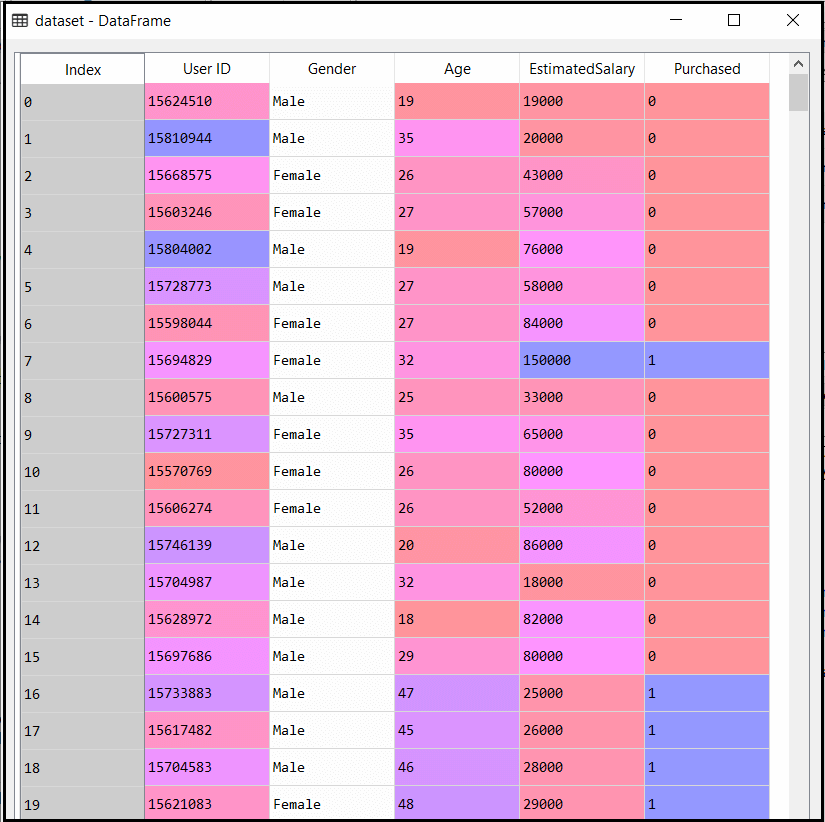
2)安装朴素贝叶斯训练集:
预处理步骤后,现在我们将适合的朴素贝叶斯模型训练集。下面是它的代码:
# Fitting Naive Bayes to the Training set
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(x_train,y_train)在上面的代码中,我们使用了GaussianNB分类到它适合的训练数据集。我们还可以使用其它分类按我们的要求。
输出:
Out[6]: GaussianNB(priors=None,var_smoothing=1e-09)3)测试集结果的预测:
现在,我们将预测的测试集的结果。对于这一点,我们将创建一个y_pred新的预测变量,将使用预测功能进行了预测。
# Predicting the Test set results
y_pred = classifier.predict(x_test)输出:
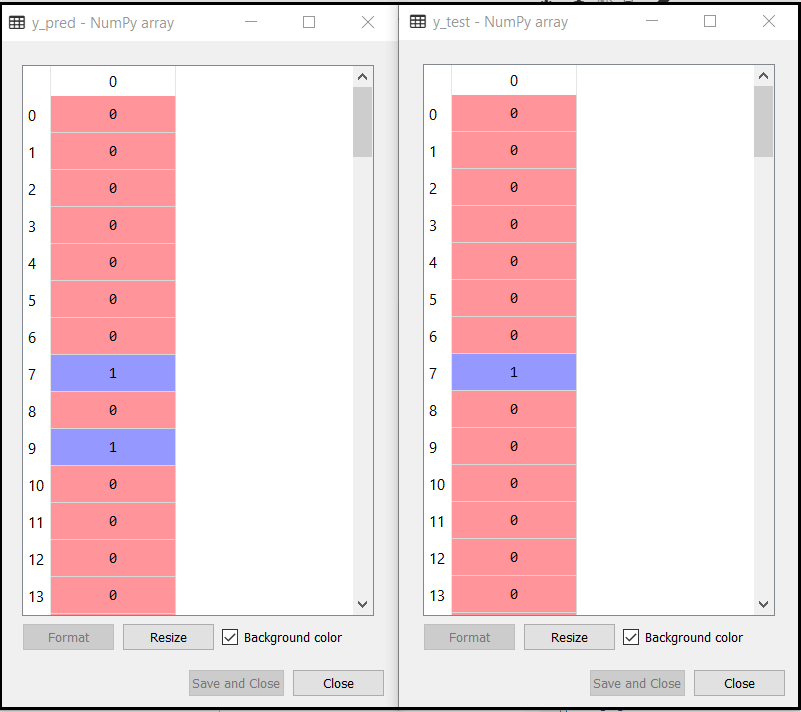
上述输出示出了用于预测矢量的结果y_pred和实数向量y_test。我们可以看到,一些断言是从真正的价值,这是不正确的预测不同。
4)创建混淆矩阵
现在,我们将检查使用混淆矩阵的朴素贝叶斯分类的准确性。下面是它的代码:
# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test,y_pred)输出:
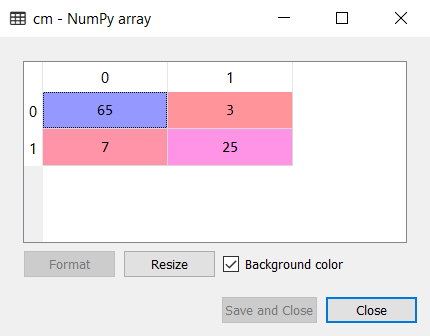
正如我们可以在上面混淆矩阵输出看到的,有7 + 3 = 10个不正确的预测,和65 + 25 = 90正确的预测。
5)可视化训练集的结果:
下一步,我们将使用朴素贝叶斯分类器的可视化训练集的结果。下面是它的代码:
# Visualising the Training set results
from matplotlib.colors import ListedColormap
x_set,y_set = x_train,y_train
X1,X2 = nm.meshgrid(nm.arange(start = x_set[:,0].min() - 1,stop = x_set[:,0].max() + 1,step = 0.01),nm.arange(start = x_set[:,1].min() - 1,stop = x_set[:,1].max() + 1,step = 0.01))
mtp.contourf(X1,X2,classifier.predict(nm.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape),alpha = 0.75,cmap = ListedColormap(('purple','green')))
mtp.xlim(X1.min(),X1.max())
mtp.ylim(X2.min(),X2.max())
for i,j in enumerate(nm.unique(y_set)):
mtp.scatter(x_set[y_set == j,0],x_set[y_set == j,1],c = ListedColormap(('purple','green'))(i),label = j)
mtp.title('Naive Bayes (Training set)')
mtp.xlabel('Age')
mtp.ylabel('Estimated Salary')
mtp.legend()
mtp.show()输出:
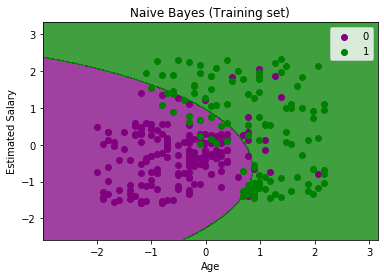
在上面的输出我们可以看到,朴素贝叶斯分类器与细界偏析的数据点。这是因为我们已经在代码中使用GaussianNB分类高斯曲线。
6)可视化的测试组的结果:
# Visualising the Test set results
from matplotlib.colors import ListedColormap
x_set,y_set = x_test,y_test
X1,X2 = nm.meshgrid(nm.arange(start = x_set[:,0].min() - 1,stop = x_set[:,0].max() + 1,step = 0.01),nm.arange(start = x_set[:,1].min() - 1,stop = x_set[:,1].max() + 1,step = 0.01))
mtp.contourf(X1,X2,classifier.predict(nm.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape),alpha = 0.75,cmap = ListedColormap(('purple','green')))
mtp.xlim(X1.min(),X1.max())
mtp.ylim(X2.min(),X2.max())
for i,j in enumerate(nm.unique(y_set)):
mtp.scatter(x_set[y_set == j,0],x_set[y_set == j,1],c = ListedColormap(('purple','green'))(i),label = j)
mtp.title('Naive Bayes (test set)')
mtp.xlabel('Age')
mtp.ylabel('Estimated Salary')
mtp.legend()
mtp.show()输出:
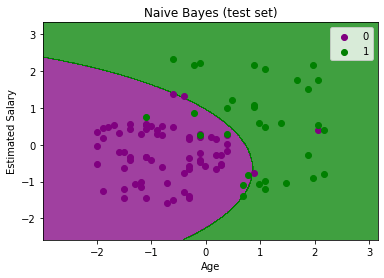
上述输出是用于测试组数据最终输出。正如我们所看到的分类创造了一个高斯曲线分割“购买”和“未购买”变量。还有我们在混淆矩阵计算了一些错误的预测。但它仍然是相当不错的分类。
 srcmini
srcmini
评论前必须登录!
注册