本文概述
我们已经讨论了回溯和骑士的巡回问题S1。让我们在迷宫作为可以使用回溯解决的另一个示例问题。
迷宫作为块的N * N二进制矩阵给出, 其中源块是最左上的块, 即maze [0] [0], 而目标块是最右下块的块, 即maze [N-1] [N-1] 。老鼠从源头开始, 必须到达目的地。老鼠只能在两个方向上移动:向前和向下。
在迷宫矩阵中, 0表示该块是死胡同, 而1表示该块可在从源到目标的路径中使用。请注意, 这是典型迷宫问题的简单版本。例如, 更复杂的版本可以是大鼠可以沿4个方向移动, 而更复杂的版本可以具有有限的移动次数。
以下是一个示例迷宫。
Gray blocks are dead ends (value = 0).
以下是上述迷宫的二进制矩阵表示。
{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}以下是具有突出解决方案路径的迷宫。
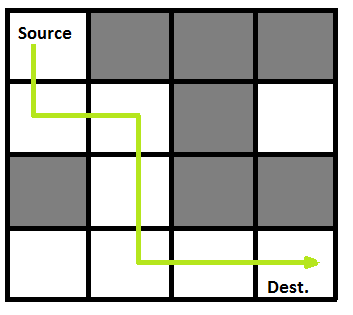
以下是上述输入矩阵的解决方案矩阵(程序的输出)。
{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}
All enteries in solution path are marked as 1.推荐:请在”实践首先, 在继续解决方案之前。
回溯算法:回溯是一种通过尝试逐步构建解决方案来递归解决问题的算法技术。一次解决一个问题, 并删除那些在任何时间点都无法满足问题约束条件的解决方案(在这里, 时间指的是直到达到搜索树的任何级别为止的时间)。回溯。
方法:形成一个递归函数, 它将遵循路径并检查路径是否到达目的地。如果路径未到达目的地, 请回溯并尝试其他路径。
算法:
- 创建一个初始为0的解决方案矩阵。
- 创建一个递归函数, 该函数需要初始矩阵, 输出矩阵和rat(i, j)的位置。
- 如果位置不在矩阵中或位置无效, 则返回。
- 将位置输出[i] [j]标记为1, 然后检查当前位置是否为目的地。如果到达目的地, 则打印输出矩阵并返回。
- 递归调用位置(i + 1, j)和(i, j + 1)。
- 未标记位置(i, j), 即output [i] [j] = 0。
C / C ++
/* C/C++ program to solve Rat in
a Maze problem using backtracking */
#include <stdio.h>
// Maze size
#define N 4
bool solveMazeUtil(
int maze[N][N], int x, int y, int sol[N][N]);
/* A utility function to print
solution matrix sol[N][N] */
void printSolution( int sol[N][N])
{
for ( int i = 0; i < N; i++) {
for ( int j = 0; j < N; j++)
printf ( " %d " , sol[i][j]);
printf ( "\n" );
}
}
/* A utility function to check if x, y is valid index for N*N maze */
bool isSafe( int maze[N][N], int x, int y)
{
// if (x, y outside maze) return false
if (
x >= 0 && x < N && y >= 0
&& y < N && maze[x][y] == 1)
return true ;
return false ;
}
/* This function solves the Maze problem
using Backtracking. It mainly uses
solveMazeUtil() to solve the problem.
It returns false if no path is possible, otherwise return true and prints the path
in the form of 1s. Please note that there
may be more than one solutions, this
function prints one of the feasible
solutions.*/
bool solveMaze( int maze[N][N])
{
int sol[N][N] = { { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 } };
if (solveMazeUtil(
maze, 0, 0, sol)
== false ) {
printf ( "Solution doesn't exist" );
return false ;
}
printSolution(sol);
return true ;
}
/* A recursive utility function
to solve Maze problem */
bool solveMazeUtil(
int maze[N][N], int x, int y, int sol[N][N])
{
// if (x, y is goal) return true
if (
x == N - 1 && y == N - 1
&& maze[x][y] == 1) {
sol[x][y] = 1;
return true ;
}
// Check if maze[x][y] is valid
if (isSafe(maze, x, y) == true ) {
// mark x, y as part of solution path
sol[x][y] = 1;
/* Move forward in x direction */
if (solveMazeUtil(
maze, x + 1, y, sol)
== true )
return true ;
/* If moving in x direction
doesn't give solution then
Move down in y direction */
if (solveMazeUtil(
maze, x, y + 1, sol)
== true )
return true ;
/* If none of the above movements
work then BACKTRACK: unmark
x, y as part of solution path */
sol[x][y] = 0;
return false ;
}
return false ;
}
// driver program to test above function
int main()
{
int maze[N][N] = { { 1, 0, 0, 0 }, { 1, 1, 0, 1 }, { 0, 1, 0, 0 }, { 1, 1, 1, 1 } };
solveMaze(maze);
return 0;
}Java
/* Java program to solve Rat in
a Maze problem using backtracking */
public class RatMaze {
// Size of the maze
static int N;
/* A utility function to print
solution matrix sol[N][N] */
void printSolution( int sol[][])
{
for ( int i = 0 ; i < N; i++) {
for ( int j = 0 ; j < N; j++)
System.out.print(
" " + sol[i][j] + " " );
System.out.println();
}
}
/* A utility function to check
if x, y is valid index for N*N maze */
boolean isSafe(
int maze[][], int x, int y)
{
// if (x, y outside maze) return false
return (x >= 0 && x < N && y >= 0
&& y < N && maze[x][y] == 1 );
}
/* This function solves the Maze problem using
Backtracking. It mainly uses solveMazeUtil()
to solve the problem. It returns false if no
path is possible, otherwise return true and
prints the path in the form of 1s. Please note
that there may be more than one solutions, this
function prints one of the feasible solutions.*/
boolean solveMaze( int maze[][])
{
int sol[][] = new int [N][N];
if (solveMazeUtil(maze, 0 , 0 , sol) == false ) {
System.out.print( "Solution doesn't exist" );
return false ;
}
printSolution(sol);
return true ;
}
/* A recursive utility function to solve Maze
problem */
boolean solveMazeUtil( int maze[][], int x, int y, int sol[][])
{
// if (x, y is goal) return true
if (x == N - 1 && y == N - 1
&& maze[x][y] == 1 ) {
sol[x][y] = 1 ;
return true ;
}
// Check if maze[x][y] is valid
if (isSafe(maze, x, y) == true ) {
// mark x, y as part of solution path
sol[x][y] = 1 ;
/* Move forward in x direction */
if (solveMazeUtil(maze, x + 1 , y, sol))
return true ;
/* If moving in x direction doesn't give
solution then Move down in y direction */
if (solveMazeUtil(maze, x, y + 1 , sol))
return true ;
/* If none of the above movements works then
BACKTRACK: unmark x, y as part of solution
path */
sol[x][y] = 0 ;
return false ;
}
return false ;
}
public static void main(String args[])
{
RatMaze rat = new RatMaze();
int maze[][] = { { 1 , 0 , 0 , 0 }, { 1 , 1 , 0 , 1 }, { 0 , 1 , 0 , 0 }, { 1 , 1 , 1 , 1 } };
N = maze.length;
rat.solveMaze(maze);
}
}
// This code is contributed by Abhishek ShankhadharPython3
# Python3 program to solve Rat in a Maze
# problem using backracking
# Maze size
N = 4
# A utility function to print solution matrix sol
def printSolution( sol ):
for i in sol:
for j in i:
print ( str (j) + " " , end = "")
print ("")
# A utility function to check if x, y is valid
# index for N * N Maze
def isSafe( maze, x, y ):
if x > = 0 and x < N and y > = 0 and y < N and maze[x][y] = = 1 :
return True
return False
""" This function solves the Maze problem using Backtracking.
It mainly uses solveMazeUtil() to solve the problem. It
returns false if no path is possible, otherwise return
true and prints the path in the form of 1s. Please note
that there may be more than one solutions, this function
prints one of the feasable solutions. """
def solveMaze( maze ):
# Creating a 4 * 4 2-D list
sol = [ [ 0 for j in range ( 4 ) ] for i in range ( 4 ) ]
if solveMazeUtil(maze, 0 , 0 , sol) = = False :
print ( "Solution doesn't exist" );
return False
printSolution(sol)
return True
# A recursive utility function to solve Maze problem
def solveMazeUtil(maze, x, y, sol):
# if (x, y is goal) return True
if x = = N - 1 and y = = N - 1 and maze[x][y] = = 1 :
sol[x][y] = 1
return True
# Check if maze[x][y] is valid
if isSafe(maze, x, y) = = True :
# mark x, y as part of solution path
sol[x][y] = 1
# Move forward in x direction
if solveMazeUtil(maze, x + 1 , y, sol) = = True :
return True
# If moving in x direction doesn't give solution
# then Move down in y direction
if solveMazeUtil(maze, x, y + 1 , sol) = = True :
return True
# If none of the above movements work then
# BACKTRACK: unmark x, y as part of solution path
sol[x][y] = 0
return False
# Driver program to test above function
if __name__ = = "__main__" :
# Initialising the maze
maze = [ [ 1 , 0 , 0 , 0 ], [ 1 , 1 , 0 , 1 ], [ 0 , 1 , 0 , 0 ], [ 1 , 1 , 1 , 1 ] ]
solveMaze(maze)
# This code is contributed by Shiv Shankar输出如下:
1值显示大鼠的路径
1 0 0 0
1 1 0 0
0 1 0 0
0 1 1 1复杂度分析:
- 时间复杂度:O(2 ^(n ^ 2))。
递归可以运行上限2 ^(n ^ 2)次。 - 空间复杂度:O(n ^ 2)。
需要输出矩阵, 因此需要大小为n * n的额外空间。
下面是此问题的扩展版本。计算迷宫中到达目的地的方式数量
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。
 srcmini
srcmini
评论前必须登录!
注册