为什么优先队列优先使用二叉堆而不是BST？

典型的优先队列需要以下操作才能有效。

1. 获取最高优先级元素(获取最小值或最大值)
2. 插入元素
3. 删除最高优先级元素
4. 降低key

一种二叉堆支持以下时间复杂度较高的操作：

1. O(1)
2. O(log n)
3. O(log n)
4. O(log n)

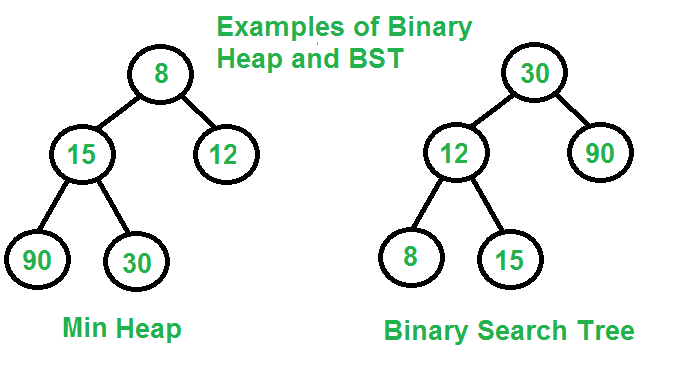
自平衡二叉搜索树, 例如AVL树, 红黑树, 等也可以同时支持上述操作。

1. 查找最小值和最大值并非自然为O(1), 但可以通过在O(1)中保留额外的指针以达到最小值或最大值, 并根据需要使用插入和删除来更新该指针, 从而轻松实现。删除后, 我们可以通过查找顺序的前任或后继来进行更新。
2. 插入元素自然是O(Logn)
3. 删除最大值或最小值也为O(log n)
4. 可以通过删除然后插入在O(Logn)中完成减小键。看到这个有关详细信息。

那么, 为什么优先使用Binary Heap？

• 由于二叉堆是使用数组实现的, 因此始终存在更好的引用局部性, 并且操作对缓存更友好。
• 尽管操作具有相同的时间复杂度, 但是二叉搜索树中的常数较高。
• 我们可以在O(n)时间内构建一个二叉堆。自平衡BST需要O(nLogn)时间来构造。
• Binary Heap不需要额外的指针空间。
• 二叉堆更易于实现。
• 像斐波那契堆这样的二叉堆有多种变体, 可以支持Θ(1)时间的插入和减小键

二叉堆总是更好吗？

尽管二叉堆是用于优先级队列的, 但BST具有自己的优点, 并且与二叉堆相比, 优点列表实际上更大。

• 在自平衡BST中搜索元素是O(Logn), 在Binary Heap中是O(n)。
• 我们可以在O(n)时间中按排序顺序打印BST的所有元素, 但是Binary Heap需要O(nLogn)时间。
• 地板和天花板可以在O(log n)时间中找到。
• 第K个最大/最小元素通过在树的O(Logn)时间中增加一个附加字段可以找到它。

本文作者：维维克·古普塔(Vivek Gupta)。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。