Floyd的慢速指针和快速指针方法如何工作？

我们已经在以下文章中讨论了Floyd的快慢指针算法检测链表中的循环.

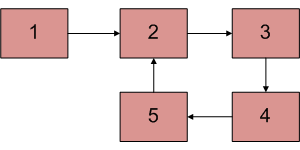
该算法是从链表的开头开始两个指针, 分别是慢速和快速。我们一次移动一个慢节点, 一次快速移动两个节点。如果有一个循环, 那么他们一定会见面的。此方法之所以有效, 是因为以下事实。

1)当慢速指针进入循环时, 快速指针必须位于循环内部。令快指针为慢指针的距离k。

2)现在, 如果考虑慢速和快速指针的移动, 我们可以注意到它们之间的距离(从慢速到快速)在每次迭代后增加一。经过一个迭代(慢=慢的下一个和快速=下一个快的下一个), 慢和快之间的距离变为k + 1, 经过两次迭代, k + 2, 依此类推。当距离变为n时, 它们会合, 因为它们以长度n的周期运动。

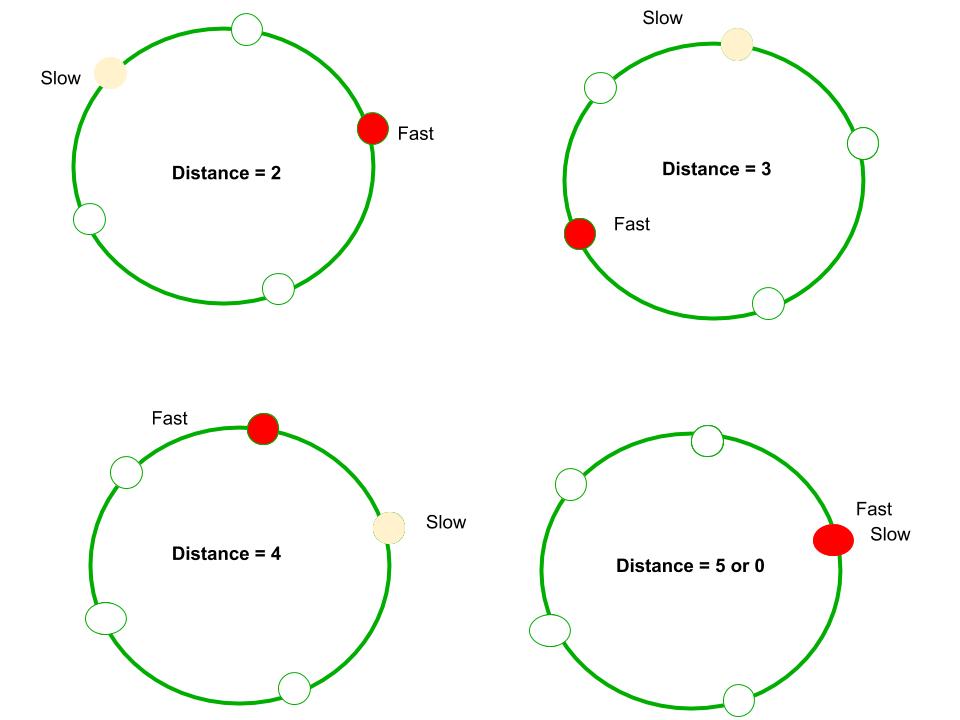
例如, 我们可以在下图中看到, 初始距离为2。经过1次迭代, 距离变为3, 经过2次迭代, 距离变为4。经过3次迭代, 它变为距离0的5。它们相遇。

循环删除算法如何工作？

请参阅的方法3

检测并删除链接列表中的循环