有关矩阵的介绍, 你可以参考以下文章:矩阵介绍
在本文中, 我们将讨论关于矩阵及其属性的各种运算:
矩阵加法–
两个矩阵A m*n和Bm*n相加得到一个矩阵Cm*n。C的元素是A和B中相应元素的和,可以表示为:

矩阵相加的算法可以写成:
for i in 1 to m
for j in 1 to n
cij = aij + bij关键点:
- 矩阵加法是可交换的, 这意味着A + B = B + A
- 矩阵的加法是关联的, 这意味着A +(B + C)=(A + B)+ C
- 矩阵A, B和A + B的顺序始终相同
- 如果A和B的顺序不同, 则无法计算A + B
- 加法运算的复杂度为O(m * n), 其中m * n是矩阵的阶数
矩阵减法–
两个矩阵Am*n和Bm*n相减得到一个矩阵Cm*n。C的元素是A和B中对应元素的差值,可以表示为:

矩阵相减的算法可写为:
for i in 1 to m
for j in 1 to n
cij = aij-bij关键点:
- 矩阵相减是不可交换的, 这意味着A-B≠B-A
- 矩阵相减是非缔合的, 这意味着A-(B-C)≠(A-B)-C
- 矩阵A, B和A-B的顺序始终相同
- 如果A和B的顺序不同, 则无法计算A-B
- 减法运算的复杂度为O(m * n), 其中m * n是矩阵的阶数
矩阵乘法–
两个矩阵Am*n和Bn*p相乘得到一个矩阵Cm*p。这意味着A的列数必须等于B的行数才能计算出C=A*B。计算元素c11时,将A的第一行元素与B的第一行元素相乘,然后相加(5*1+6*4),结果如下:
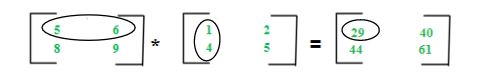
矩阵A与阶m * n相乘而矩阵B与阶n * p相乘的算法可以写成:
for i in 1 to m
for j in 1 to p
cij = 0
for k in 1 to n
cij += aik*bkj关键点:
- 矩阵的乘法是不可交换的, 这意味着A * B≠B * A
- 矩阵相乘是关联的, 这意味着A *(B * C)=(A * B)* C
- 为了计算A * B, A中的列数必须等于B中的行数
- A * B的存在并不意味着B * A的存在
- 乘法运算的复杂度(A * B)为O(m * n * p), 其中m * n和n * p分别为A和B的阶数
- 计算为A * B的矩阵C的阶为m * p, 其中m * n和n * p分别为A和B的阶
接下来阅读–矩阵的行列式, 矩阵的伴随和逆
 srcmini
srcmini
评论前必须登录!
注册