本文概述
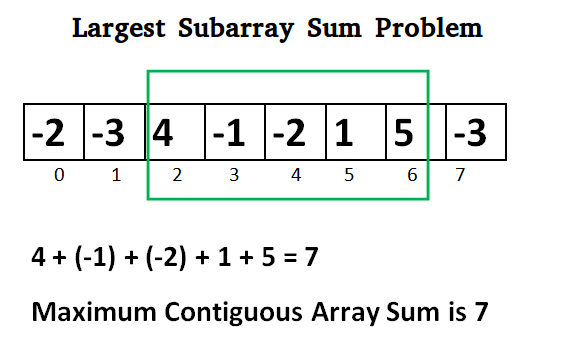
编写一个有效的程序, 以在具有最大和的一维数字数组中找到连续子数组的和。
python
# Python program to find maximum contiguous subarray
# Function to find the maximum contiguous subarray
from sys import maxint
def maxSubArraySum(a, size):
max_so_far = - maxint - 1
max_ending_here = 0
for i in range ( 0 , size):
max_ending_here = max_ending_here + a[i]
if (max_so_far <max_ending_here):
max_so_far = max_ending_here
if max_ending_here <0 :
max_ending_here = 0
return max_so_far
# Driver function to check the above function
a = [ - 13 , - 3 , - 25 , - 20 , - 3 , - 16 , - 23 , - 12 , - 5 , - 22 , - 15 , - 4 , - 7 ]
print "Maximum contiguous sum is" , maxSubArraySum(a, len (a))
# This code is contributed by _Devesh Agrawal_输出如下:
Maximum contiguous sum is -3如果我们将max_so_far与max_ending_here进行比较, 则仅当max_ending_here大于0时, 才能进一步优化上述程序。
python
def maxSubArraySum(a, size):
max_so_far = 0
max_ending_here = 0
for i in range ( 0 , size):
max_ending_here = max_ending_here + a[i]
if max_ending_here <0 :
max_ending_here = 0
# Do not compare for all elements. Compare only
# when max_ending_here> 0
elif (max_so_far <max_ending_here):
max_so_far = max_ending_here
return max_so_far请参考完整的文章最大总和连续子数组更多细节!
 srcmini
srcmini
评论前必须登录!
注册