本文概述
- DFA是指确定性有限自动机。确定性是指计算的唯一性。如果将机器一次读取一个符号的输入字符串,则该有限自动机称为确定性有限自动机。
- 在DFA中,从当前状态到下一个状态的特定输入只有一条路径。
- DFA不接受无效移动,即DFA在没有任何输入字符的情况下无法更改状态。
- DFA可以包含多个最终状态。它在编译器的词法分析中使用。
在下图中,我们可以看到从输入a的状态q0开始,只有一条路径通向q1。类似地,从q0开始,输入b只有一条路径通向q2。
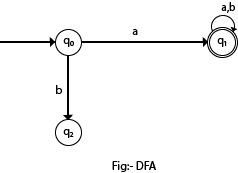
DFA的正式定义
DFA是5个元组的集合,与我们在FA定义中描述的相同。
Q: finite set of states
∑: finite set of the input symbol
q0: initial state
F: final state
δ: Transition function过渡函数可以定义为:
δ: Q x ∑→QDFA的图形表示
DFA可以由称为状态图的有向图表示。其中:
- 状态由顶点表示。
- 标有输入字符的弧线显示过渡。
- 初始状态用箭头标记。
- 最终状态由双圆圈表示。
范例1:
Q = {q0, q1, q2}
∑ = {0, 1}
q0 = {q0}
F = {q2}解:
过渡图:

转换表:
| 现状 | 输入0的下一个状态 | 输入1的下一个状态 |
|---|---|---|
| →q0 | 00 | 11 |
| q1 | 22 | 11 |
| *q2 | 22 | 22 |
范例2:
∑ = {0,1}的DFA接受以0开头的所有数字。
解:
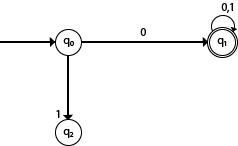
说明:
- 在上图中,我们可以看到在给定状态为0的DFA输入0时,DFA会将状态更改为q1,并在开始输入0时始终进入最终状态q1。它可以接受00、01、000、001 … 。等等。它不能接受任何以1开头的字符串,因为它永远不会进入以1开头的字符串的最终状态。
范例3:
∑ = {0,1}的DFA接受所有以0结尾的。
解:

说明:
在上图中,我们可以看到,在状态q0下给定0作为DFA的输入时,DFA将状态更改为q1。它可以接受任何以0结尾的字符串,例如00、10、110、100等。它不能接受任何以1结尾的字符串,因为它永远不会在1个输入上进入最终状态q1,因此以1结尾的字符串将不被接受或被拒绝。
 srcmini
srcmini
评论前必须登录!
注册