确定性有限自动机的例子

范例1：

设计一个∑ = {0，1}的FA接受那些以1开头和0结束的字符串。

解：

FA将具有开始状态q0，只有输入1的边沿将从该状态进入下一个状态。

在状态q1中，如果我们读取1，则将处于状态q1，但是在状态q1中如果读取0，则将到达状态q2，这是最终状态。在状态q2中，如果我们读取0或1，我们将分别进入q2状态或q1状态。请注意，如果输入以0结尾，它将处于最终状态。

范例2：

设计一个∑ = {0，1}的FA接受唯一的输入101。

解：

在给定的解决方案中，我们可以看到只有输入101将被接受。因此，对于输入101，没有显示其他输入的其他路径。

范例3：

∑ = {0，1}的设计FA接受偶数0和1的偶数。

解：

该FA将考虑输入0和输入1的四个不同阶段。这些阶段可能是：

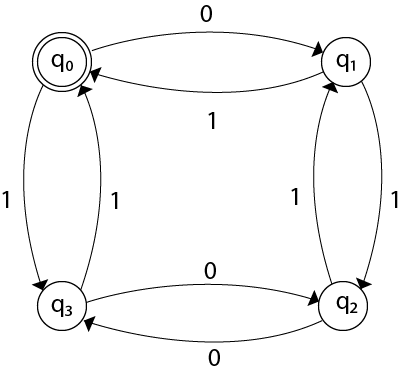
q0是开始状态，也是最终状态。请注意，保持0和1的对称性。我们可以将含义与每个州相关联：

q0：0的偶数和1的偶数的状态。 q1：奇数0和偶数1的状态。 q2：0的奇数和1的奇数的状态。 q3：偶数0和奇数1的状态。

范例4：

∑ = {0，1}的设计FA接受具有三个连续0的所有字符串的集合。

解：

将为该特定语言生成的字符串是000、0001、1000、10001，…。其中0总是以3的形式出现。过渡图如下：

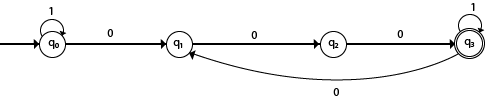
注意，三重零序列保持最终状态。

范例5：

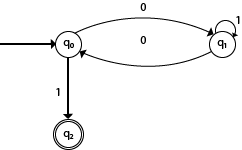
设计DFA L（M）= {w | wε{0，1} *}，并且W是不包含连续1的字符串。

解：

当三个连续的1出现时，DFA将为：

这里两个连续的1或单个1是可以接受的，因此

阶段q0，q1，q2是最终状态。 DFA会生成不包含连续1（例如10、110、101等）的字符串。

范例6：

设计一个∑ = {0，1}的FA接受偶数为0的字符串，后跟单个1。

解：

DFA可以通过过渡图显示为：