本文概述
- NFA代表非确定性有限自动机。对于给定的常规语言,构造一个NFA比DFA容易。
- 当存在从当前状态到下一个状态的特定输入存在许多路径时,有限自动机称为NFA。
- 每个NFA都不是DFA,但是每个NFA都可以转换为DFA。
- NFA的定义方式与DFA相同,但以下两个例外除外,它包含多个下一个状态,并且包含ε过渡。
在下图中,我们可以看到从输入a的状态q0开始,有两个下一个状态q1和q2,类似地,从输入b的q0开始,下一个状态是q0和q1。因此,对于特定的输入,下一步是不确定的还是确定的。因此,该FA被称为非确定性有限自动机。
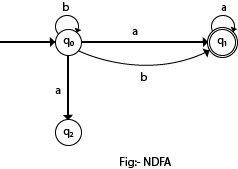
NFA的正式定义
NFA还具有与DFA相同的五个状态,但具有不同的过渡功能,如下所示:
δ: Q x ∑ →2Q哪里,
Q: finite set of states
∑: finite set of the input symbol
q0: initial state
F: final state
δ: Transition functionNFA的图形表示
NFA可以由称为状态图的有向图表示。其中:
- 状态由顶点表示。
- 标有输入字符的弧线显示过渡。
- 初始状态用箭头标记。
- 最终状态由双圆圈表示。
范例1:
Q = {q0, q1, q2}
∑ = {0, 1}
q0 = {q0}
F = {q2}解:
过渡图:

转换表:
| 现状 | 输入0的下一个状态 | 输入1的下一个状态 |
|---|---|---|
| →q0 | q0, q1 | 11 |
| q1 | 22 | 00 |
| *q2 | 22 | q1, q2 |
在上图中,我们可以看到,当当前状态为q0时,在输入0上,下一个状态将为q0或q1,在输入1时,下一个状态将为q1。当前状态为q1时,在输入0时,下一个状态将为q2,在输入1时,下一个状态将为q0。当前状态为q2时,输入0时,下一个状态为q2,输入1时,下一个状态为q1或q2。
范例2:
∑ = {0,1}的NFA接受所有带有01的字符串。
解:

转换表:
| 现状 | 输入0的下一个状态 | 输入1的下一个状态 |
|---|---|---|
| →q0 | 11 | Ë |
| q1 | Ë | 22 |
| *q2 | 22 | 22 |
范例3:
NFA,∑ = {0,1},并接受所有长度至少为2的字符串。
解:
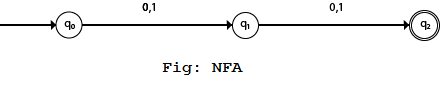
转换表:
| 现状 | 输入0的下一个状态 | 输入1的下一个状态 |
|---|---|---|
| →q0 | 11 | 11 |
| q1 | 22 | 22 |
| *q2 | Ë | Ë |
 srcmini
srcmini
评论前必须登录!
注册